您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了Python遞歸下降Parser怎么實現的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇Python遞歸下降Parser怎么實現文章都會有所收獲,下面我們一起來看看吧。
要解析這類文本,需要另外一種特定的語法規則。我們這里介紹可以表示上下文無關文法(context free grammer)的語法規則巴科斯范式(BNF)和擴展巴科斯范式(EBNF)。實際上,小到一個算術運算表達式,大到幾乎所有程序設計語言,都是通過上下文無關文法來定義的。
對于簡單的算術運算表達式,假定我們已經用分詞技術將其轉化為輸入的tokens流,如NUM+NUM*NUM(分詞方法參見上一篇博文)。
在此基礎上,我們定義BNF規則定義如下:
expr ::= expr + term | expr - term | term term ::= term * factor | term / factor | factor factor ::= (expr) | NUM
當然,這種計法還不夠簡潔明了,我們實際采用的為EBNF形式:
expr ::= term { (+|-) term }*
term ::= factor { (*|/) factor }*
factor ::= (expr)
| NUMBNF和EBNF每一條規則(形如::=的式子)都可以看做是一種替換,即左側的符號可以被右側的符號所替換。而解析的過程中我們嘗試將輸入文本同語法規則做匹配,通過BNF/EBNF來完成各種替換和擴展。其中,EBNF中包含在{...}*中的規則是可選的,*意味著零個或多個重復項(參考正則表達式)。
下圖形象地展示了遞歸下降解析器(parser)中“遞歸”和“下降”部分和ENBF的關系:
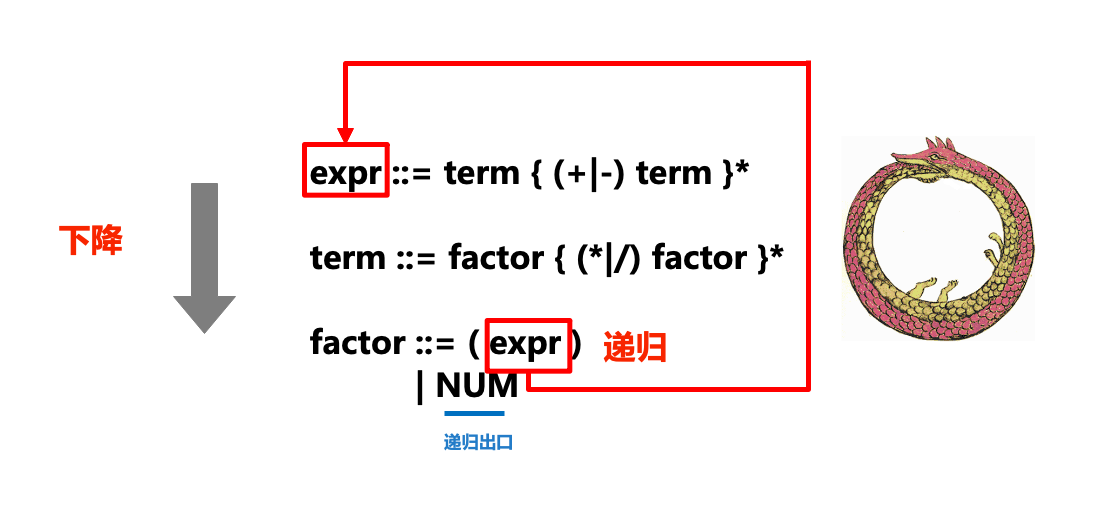
在實際的解析過程中,我們對tokens流從左到右進行掃描,在掃描的過程中處理token,如果卡住就產生一個語法錯誤。對于規則,我們將每一條語法規則轉變為一個函數或方法,比如上面的ENBF規則就轉換為下列的方法:
class ExpressionEvaluator(): ... def expr(self): ... def term(self): ... def factor(self): ...
在調用某個規則對應方法的過程中,如果我們發現接下來的符號需要采用另一個規則來匹配,則我們就會“下降”到另一個規則方法(如在expr中調用term,term中調用factor),則也就是遞歸下降中“下降”的部分。
有時也會調用已經在執行的方法(比如在expr中調用term,term中調用factor后,又在factor中調用expr,相當于一條銜尾蛇),這也就是遞歸下降中“遞歸”的部分。
對于語法中出現的重復部分(例如expr ::= term { (+|-) term }*),我們則通過while循環來實現。
下面我們來看具體的代碼實現。首先是分詞部分,我們參照上一篇介紹分詞博客的代碼。
import re
import collections
# 定義匹配token的模式
NUM = r'(?P<NUM>\d+)' # \d表示匹配數字,+表示任意長度
PLUS = r'(?P<PLUS>\+)' # 注意轉義
MINUS = r'(?P<MINUS>-)'
TIMES = r'(?P<TIMES>\*)' # 注意轉義
DIVIDE = r'(?P<DIVIDE>/)'
LPAREN = r'(?P<LPAREN>\()' # 注意轉義
RPAREN = r'(?P<RPAREN>\))' # 注意轉義
WS = r'(?P<WS>\s+)' # 別忘記空格,\s表示空格,+表示任意長度
master_pat = re.compile(
'|'.join([NUM, PLUS, MINUS, TIMES, DIVIDE, LPAREN, RPAREN, WS]))
# Tokenizer
Token = collections.namedtuple('Token', ['type', 'value'])
def generate_tokens(text):
scanner = master_pat.scanner(text)
for m in iter(scanner.match, None):
tok = Token(m.lastgroup, m.group())
if tok.type != 'WS': # 過濾掉空格符
yield tok下面是表達式求值器的具體實現:
class ExpressionEvaluator():
""" 遞歸下降的Parser實現,每個語法規則都對應一個方法,
使用 ._accept()方法來測試并接受當前處理的token,不匹配不報錯,
使用 ._except()方法來測試當前處理的token,并在不匹配的時候拋出語法錯誤
"""
def parse(self, text):
""" 對外調用的接口 """
self.tokens = generate_tokens(text)
self.tok, self.next_tok = None, None # 已匹配的最后一個token,下一個即將匹配的token
self._next() # 轉到下一個token
return self.expr() # 開始遞歸
def _next(self):
""" 轉到下一個token """
self.tok, self.next_tok = self.next_tok, next(self.tokens, None)
def _accept(self, tok_type):
""" 如果下一個token與tok_type匹配,則轉到下一個token """
if self.next_tok and self.next_tok.type == tok_type:
self._next()
return True
else:
return False
def _except(self, tok_type):
""" 檢查是否匹配,如果不匹配則拋出異常 """
if not self._accept(tok_type):
raise SyntaxError("Excepted"+tok_type)
# 接下來是語法規則,每個語法規則對應一個方法
def expr(self):
""" 對應規則: expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一項
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一項是"+"或"-"
op = self.tok.type
# 再取下一項,即運算符右值
right = self.term()
if op == "PLUS":
exprval += right
elif op == "MINUS":
exprval -= right
return exprval
def term(self):
""" 對應規則: term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一項
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一項是"+"或"-"
op = self.tok.type
# 再取下一項,即運算符右值
right = self.factor()
if op == "TIMES":
termval *= right
elif op == "DIVIDE":
termval /= right
return termval
def factor(self):
""" 對應規則: factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 遞歸出口
return int(self.tok.value)
elif self._accept("LPAREN"):
exprval = self.expr() # 繼續遞歸下去求表達式值
self._except("RPAREN") # 別忘記檢查是否有右括號,沒有則拋出異常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")我們輸入以下表達式進行測試:
e = ExpressionEvaluator()
print(e.parse("2"))
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))求值結果如下:
2
5
14
37
如果我們輸入的文本不符合語法規則:
print(e.parse("2 + (3 + * 4)"))則會拋出SyntaxError異常:Expected NUMBER or LPAREN。
綜上,可見我們的表達式求值算法運行正確。
上面我們是得到表達式的結果,但是如果我們想分析表達式的結構,生成一棵簡單的表達式解析樹呢?那么我們需要對上述類的方法做一定修改:
class ExpressionTreeBuilder(ExpressionEvaluator):
def expr(self):
""" 對應規則: expression ::= term { ('+'|'-') term }* """
exprval = self.term() # 取第一項
while self._accept("PLUS") or self._accept("DIVIDE"): # 如果下一項是"+"或"-"
op = self.tok.type
# 再取下一項,即運算符右值
right = self.term()
if op == "PLUS":
exprval = ('+', exprval, right)
elif op == "MINUS":
exprval -= ('-', exprval, right)
return exprval
def term(self):
""" 對應規則: term ::= factor { ('*'|'/') factor }* """
termval = self.factor() # 取第一項
while self._accept("TIMES") or self._accept("DIVIDE"): # 如果下一項是"+"或"-"
op = self.tok.type
# 再取下一項,即運算符右值
right = self.factor()
if op == "TIMES":
termval = ('*', termval, right)
elif op == "DIVIDE":
termval = ('/', termval, right)
return termval
def factor(self):
""" 對應規則: factor ::= NUM | ( expr ) """
if self._accept("NUM"): # 遞歸出口
return int(self.tok.value) # 字符串轉整形
elif self._accept("LPAREN"):
exprval = self.expr() # 繼續遞歸下去求表達式值
self._except("RPAREN") # 別忘記檢查是否有右括號,沒有則拋出異常
return exprval
else:
raise SyntaxError("Expected NUMBER or LPAREN")輸入下列表達式測試一下:
print(e.parse("2+3"))
print(e.parse("2+3*4"))
print(e.parse("2+(3+4)*5"))
print(e.parse('2+3+4'))以下是生成結果:
('+', 2, 3)
('+', 2, ('*', 3, 4))
('+', 2, ('*', ('+', 3, 4), 5))
('+', ('+', 2, 3), 4)
可以看到表達式樹生成正確。
我們上面的這個例子非常簡單,但遞歸下降的解析器也可以用來實現相當復雜的解析器,例如Python代碼就是通過一個遞歸下降解析器解析的。您要是對此跟感興趣可以檢查Python源碼中的Grammar文件來一探究竟。然而,下面我們接著會看到,自己動手寫一個解析器會面對各種陷阱和挑戰。
任何涉及左遞歸形式的語法規則,都沒法用遞歸下降parser來解決。所謂左遞歸,即規則式子右側最左邊的符號是規則頭,比如對于以下規則:
items ::= items ',' item | item
完成該解析你可能會定義以下方法:
def items(self):
itemsval = self.items() # 取第一項,然而此處會無窮遞歸!
if itemsval and self._accept(','):
itemsval.append(self.item())
else:
itemsval = [self.item()]這樣做會在第一行就無窮地調用self.items()從而產生無窮遞歸錯誤。
還有一種是語法規則自身的錯誤,比如運算符優先級。我們如果忽視運算符優先級直接將表達式簡化如下:
expr ::= factor { ('+'|'-'|'*'|'/') factor }*
factor ::= '(' expr ')'
| NUMPYTHON 復制 全屏
這個語法從技術上可以實現,但是沒有遵守計算順序約定,導致"3+4*5"的運算結果為35,而不是預期的23。故此處需要用獨立的expr和term規則來確保計算結果的正確性。
關于“Python遞歸下降Parser怎么實現”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“Python遞歸下降Parser怎么實現”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。