您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容主要講解“java弗洛伊德算法與迪杰斯特拉算法的實例介紹”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“java弗洛伊德算法與迪杰斯特拉算法的實例介紹”吧!
公交和地鐵是最普遍的交通工具了,但是通常情況下去往某處有多種出行方案,有的少換乘,有的時間短,有的步行少,等等。這就涉及到如何尋找一條最合適的路徑的問題,比如從下圖的v<sub>0</sub>處出發,怎樣才能最快到達v<sub>8</sub>處?
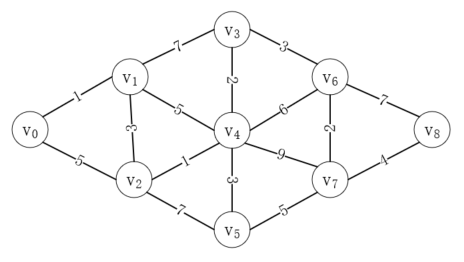
尋找最短路徑,通常也有兩種經典算法,接下來我們一一介紹。
迪杰斯特拉算法的思路是從起點開始,尋找它到每個中間點的最短距離,一步步向終點逼近。我們就以上圖為例,演示迪杰斯特拉算法的過程。
首先從v<sub>0</sub>出發,可以到達的最近的點是v<sub>1</sub>,距離是1,所以通過的第一條邊是(v<sub>0</sub>, v<sub>1</sub>),如下所示:
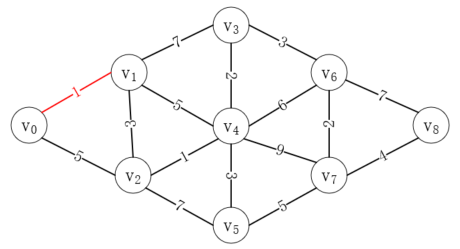
接下來因為v<sub>1</sub>可以去往v<sub>2</sub>、v<sub>3</sub>和v<sub>4</sub>,所以從v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>距離為4,從v<sub>0</sub>->v<sub>1</sub>->v<sub>3</sub>距離為8,從v<sub>0</sub>->v<sub>1</sub>->v<sub>4</sub>距離為6,這三條路徑中最短為v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>,它甚至比直接從v<sub>0</sub>->v<sub>2</sub>還要短,所以接下來的路徑應該為v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>,如下所示:
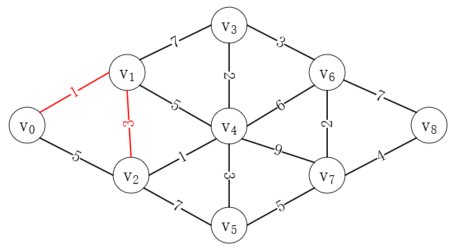
接下來我們又可以獲取更多的路徑信息,從v<sub>0</sub>->v<sub>2</sub>->v<sub>4</sub>距離是5,從v<sub>0</sub>->v<sub>2</sub>->v<sub>5</sub>距離是11,而前者比從從v<sub>0</sub>->v<sub>1</sub>->v<sub>4</sub>還要短,所以接下來的路徑應該為v<sub>0</sub>->v<sub>2</sub>->v<sub>4</sub>,其中v<sub>0</sub>->v<sub>2</sub>實際上是v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>,如下所示:
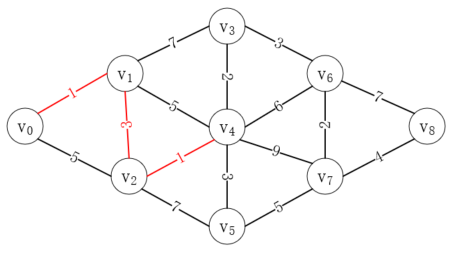
接下來,我們按照同樣的邏輯,從v<sub>4</sub>出發最近的頂點為v<sub>3</sub>,路徑長度為7,而從v<sub>0</sub>->v<sub>1</sub>->v<sub>3</sub>的直接距離為8,所以完整路徑為v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>->v<sub>4</sub>->v<sub>3</sub>,如下所示:
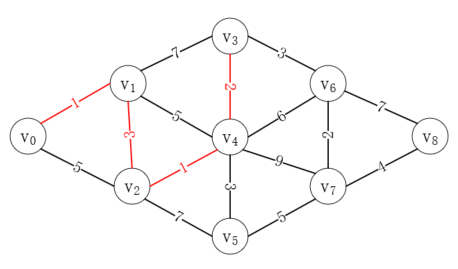
按照同樣方式,我們可以得到以下路徑,就是我們要找的最短路徑,如下所示:
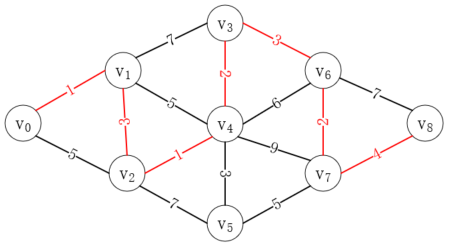
可以看到,迪杰斯特拉算法就是通過不斷尋找到中間頂點的最短距離和對比頂點間的直接距離,一點點逼近終點的,這比較適合于提前規劃好路線,而不能走一步看一步。
弗洛伊德算法比較精妙,但是也相對較難理解,我們依然以上圖為例,演示它的運算過程。
首先,構建它的鄰接矩陣表,稱為D<sup>-1</sup>,除此之外,再構建一個矩陣P<sup>-1<sup>,賦值如下:
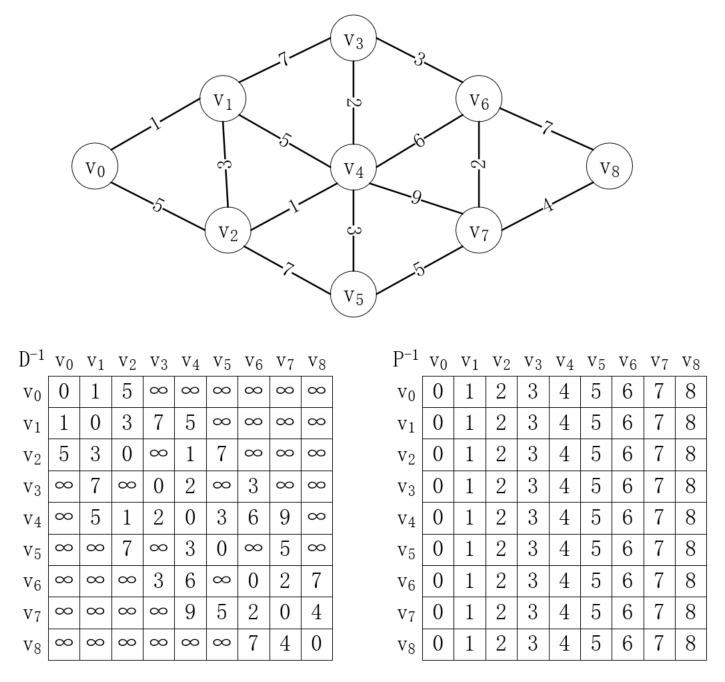
其中上標-1表示初始化狀態,P<sup>-1</sup>中的每個值表示從頂點 v<sub>i</sub> 到頂點 v<sub>j</sub> 需要經過的中間點,默認值表示直接連接,沒有中間點。
初始化完成后,就可以進行弗洛伊德算法了。首先,讓所有頂點之間的路徑都經過v<sub>0</sub>,比如從v<sub>1</sub>->v<sub>2</sub>,變為v<sub>1</sub>->v<sub>0</sub>->v<sub>2</sub>,此時發現v<sub>1</sub>->v<sub>2</sub>距離為3,而變為v<sub>1</sub>->v<sub>0</sub>->v<sub>2</sub>后距離成為了6,所以不需要更新數據。由于v<sub>3</sub>-v<sub>8</sub>都不鄰接于v<sub>0</sub>,也就無法讓 v<sub>0</sub> 成為中間點,所以也不需要更新,因此這次操作后,數據沒有任何改變,但是矩陣的狀態改變了,從D<sup>-1</sup>變為D<sup>0</sup>,P同理,如下所示:

現在,我們以每個頂點之間的路徑都經過v<sub>1</sub>,可以看到v<sub>0</sub>->v<sub>2</sub>的距離為5,而v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>的距離為4,比直接距離更短,同理v<sub>0</sub>->v<sub>3</sub>原本不能直接到達,經過v<sub>1</sub>后的路徑v<sub>0</sub>->v<sub>1</sub>->v<sub>3</sub>距離變為8,v<sub>0</sub>->v<sub>1</sub>->v<sub>4</sub>距離變為6。以v<sub>2</sub>為起點,到達v<sub>3</sub>的路徑v<sub>2</sub>->v<sub>1</sub>->v<sub>3</sub>距離變為10。以v<sub>3</sub>為起點,到達v<sub>0</sub>和v<sub>2</sub>的距離,以及以v<sub>4</sub>為起點,到達v<sub>0</sub>的距離都發生了改變。此時因為將v<sub>1</sub>作為中間點,使得部分路徑縮短,于是更新兩個表的值如下:
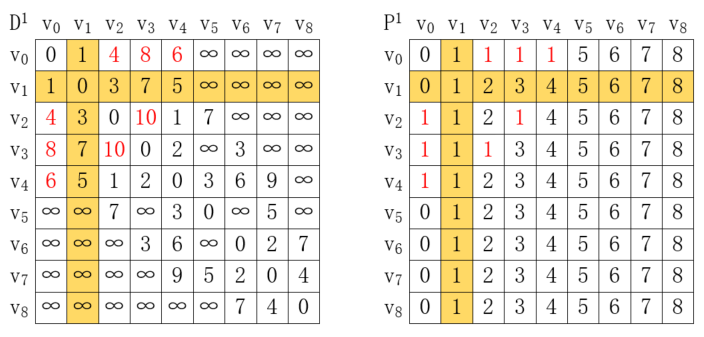
其中P的某些值更新為1,表示從v<sub>i</sub>到v<sub>j</sub>需要經過頂點v<sub>1</sub>。
在此基礎上,我們以每個頂點之間的路徑都經過v<sub>2</sub>,再次進行同樣的計算,我們找到的第一個需要更新的數據是v<sub>0</sub>->v<sub>4</sub>,它的距離是6,而v<sub>0</sub>->v<sub>2</sub>->v<sub>4</sub>的距離為5,所以D[0][4]值更新為5,P[0][4]的值則應該更新為P[0][2]的值,這是因為從v<sub>0</sub>->v<sub>2</sub>還有可能經過其它中間點,例如這里就是經過v<sub>1</sub>,這樣我們就把v<sub>0</sub>->v<sub>4</sub>的路徑從原本的v<sub>0</sub>->...->v<sub>4</sub>,變為了從v<sub>0</sub>->...->v<sub>2</sub>->v<sub>4</sub>,只要不斷迭代,就可以找到完整的路徑。更新結果如下所示:
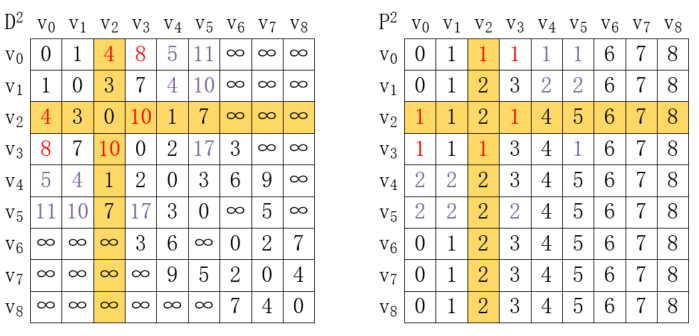
按照同樣的規則,我們對其余數據進行同樣的操作,最終可以得到下圖的結果:
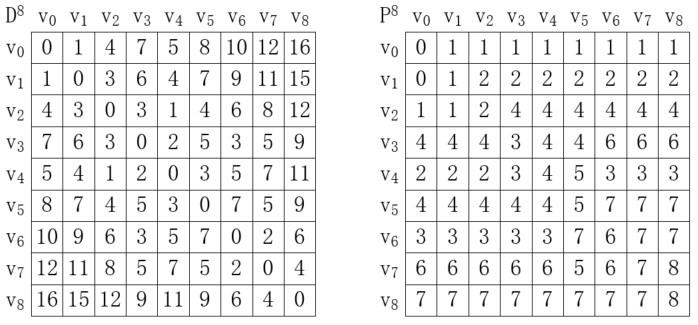
最后得到的D<sup>8</sup>表的每個數據表示從頂點 v<sub>i</sub> 到頂點 v<sub>j</sub> 的最短距離,而P<sup>8</sup>表的每個數據表示從頂點 v<sub>i</sub> 到頂點 v<sub>j</sub> 需要經過的第一個中間頂點。例如從 v<sub>0</sub>->v<sub>8</sub>,首先要經過頂點 v<sub>1</sub>,完整路徑為v<sub>0</sub>->v<sub>1</sub>加上v<sub>1</sub>->v<sub>8</sub>,而v<sub>1</sub>->v<sub>8</sub>需要經過v<sub>2</sub>,于是完整路徑為v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>加上v<sub>2</sub>->v<sub>8</sub>,迭代下去,可以得到最終的最短路徑為v<sub>0</sub>->v<sub>1</sub>->v<sub>2</sub>->v<sub>4</sub>->v<sub>3</sub>->v<sub>6</sub>->v<sub>7</sub>->v<sub>8</sub>,如下所示:
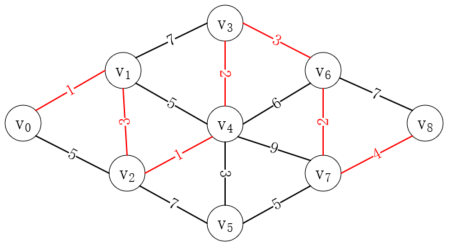
可以看到,結果和使用迪杰斯特拉算法的結果是一致的。
public void dijkstra(AMGraph<String> amGraph, int fromIndex) {
int len = amGraph.getVertexNum();
// 存儲從fromIndex到其他各頂點的最短路徑下標
int[] p = new int[len];
// 存儲從fromIndex到其他各頂點的最短路徑的權值和
int[] d = new int[len];
// 標記求得了頂點fromIndex到其他各定點的最短路徑
boolean[] finded = new boolean[len];
// 初始化數據
for (int toIndex = 0; toIndex < len; toIndex++) {
finded[toIndex] = false;
d[toIndex] = amGraph.getWeight(fromIndex, toIndex);
p[toIndex] = 0;
}
// fromIndex到自己的路徑長度為0,并且不需要再求它的最短路徑了
d[fromIndex] = 0;
finded[fromIndex] = true;
int min = 0;
int k = -1;
// 求fromIndex到toIndex的最短路徑
for (int toIndex = 1; toIndex < len; toIndex++) {
min = Integer.MAX_VALUE;
// 尋找距離fromIndex最近的頂點
for (int i = 0; i < len; i++) {
if (!finded[i] && d[i] < min) {
// i 離 fromIndex最近
k = i;
min = d[i];
}
}
// 找到了最近的點
finded[k] = true;
// 更新剩余頂點的距離值
for (int i = 0; i < len; i++) {
// 如果經過 k 之后的距離比直接到 i 的距離近,就更新距離
if (!finded[i] && amGraph.getWeight(k, i) != Integer.MAX_VALUE && (min + amGraph.getWeight(k, i) < d[i])) {
d[i] = min + amGraph.getWeight(k, i);
p[i] = k;
}
}
System.out.println();
for (int i = 0; i < len; i++) {
System.out.print(p[i] + "\t");
}
}
}迪杰斯特拉算法的時間復雜度為O(n<sup>2</sup>),但是它每次只能計算出從某一個頂點開始到其它頂點的最短路徑。
public void floyd(AMGraph<String> amGraph) {
int len = amGraph.getVertexNum();
int[][] d = new int[len][len];
int[][] p = new int[len][len];
// 初始化d和p數組
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
d[i][j] = amGraph.getWeight(i, j);
p[i][j] = j;
}
}
for (int k = 0; k < len; k++) {
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
if (d[i][k] != Integer.MAX_VALUE && d[k][j] != Integer.MAX_VALUE && d[i][j] > d[i][k] + d[k][j]) {
d[i][j] = d[i][k] + d[k][j];
p[i][j] = p[i][k];
}
}
}
}
printD(len, d);
printP(len, p);
}弗洛伊德算法十分優雅和簡潔,并且可以得到任意頂點間的最短路徑,不過因為三層循環的原因,它的時間復雜度為O(n<sup>3</sup>)。
以上涉及代碼請參考ShortestPath.java。
到此,相信大家對“java弗洛伊德算法與迪杰斯特拉算法的實例介紹”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。