您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“java中普里姆算法與克魯斯卡爾算法的實例介紹”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
我們已經掌握了圖的概念和基本操作,接下來了解一下圖可以解決的問題。圖主要用來解決多對多問題,比如有多個起點和終點,或者有多種選擇的問題。例如我們要從下圖中找到能連通每個頂點的最短路徑,或者尋找從頂點v<sub>0</sub>到頂點v<sub>3</sub>的最短路徑:
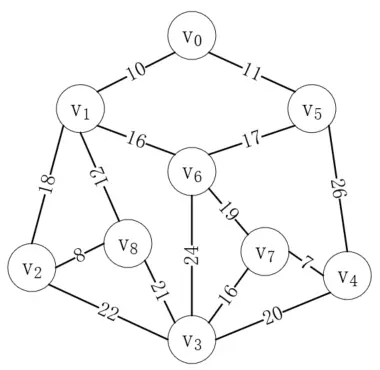
現在我們要研究的就是尋找能連通每個頂點的最短路徑,我們稱這種構造連通網的最小代價生成樹為最小生成樹。這個問題有兩個經典的算法,分別是普里姆算法和克魯斯卡爾算法。
普里姆算法的思想是每次都從未選擇的頂點中選擇代價最小的頂點,并更新剩余頂點的最小代價值。我們以上圖為例,演示普里姆算法的過程。
首先選擇一個頂點,比如v<sub>0</sub>,與v<sub>0</sub>相連的頂點記它的最小代價值為實際值,其余頂點記為∞,如下所示:
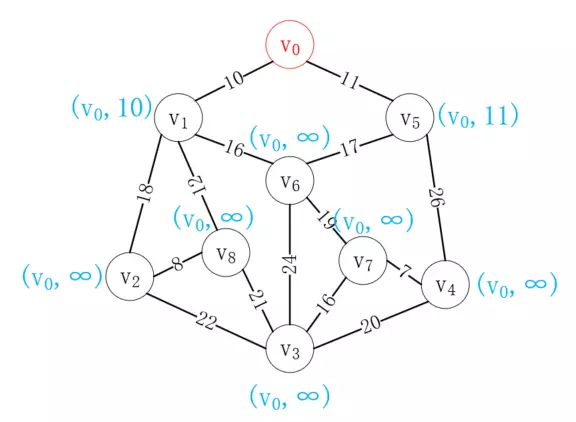
接下來選擇距離v<sub>0</sub>最近的頂點v<sub>1</sub>加入已選列表,并更新剩余結點到已選列表的距離值,如下所示:
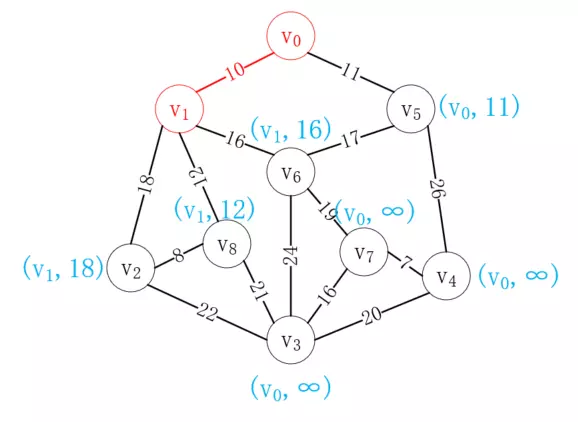
接下來再次選擇距離已選列表最近的頂點,很顯然v<sub>5</sub>最近,選擇后結果如下:
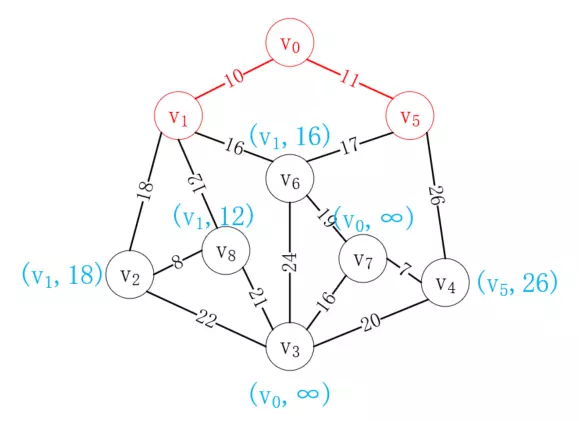
按照同樣的方式,我們選擇v<sub>8</sub>加入已選列表,如下所示:
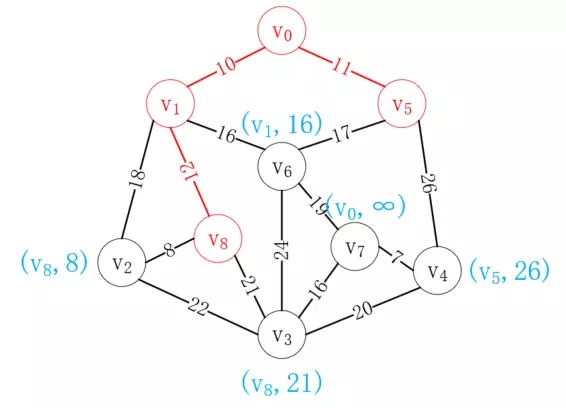
重復這一操作,最后我們可以得到如下路徑,就是我們要構造的最小生成樹:
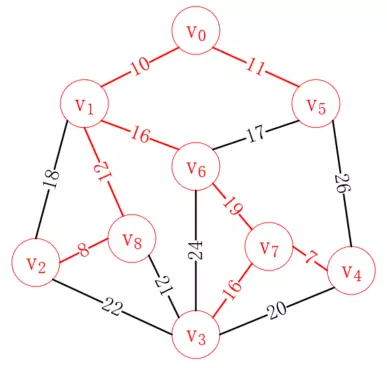
普里姆算法是從頂點出發,我們也可以從邊出發,克魯斯卡爾算法就是每次選擇合適的最小的邊加入已選列表,直至所有頂點都連通。我們依然以上圖為例,演示它的過程。
因為要對邊進行操作,所以首先應該對所有的邊按照代價大小排序,還記得圖的邊集數組存儲方式嗎?我們把邊排序后就放在一個邊集數組中,如下所示:
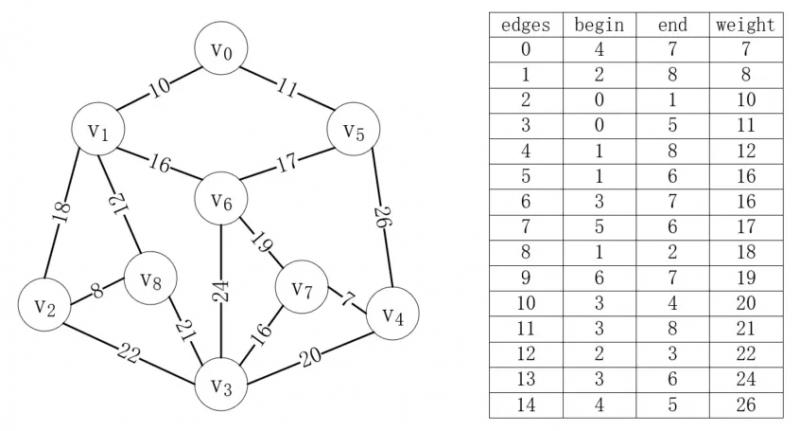
首先,我們把每個頂點都看作一棵獨立的樹,這些頂點組成了一個森林,而我們的目的就是把這個森林組合成一棵樹,如下所示:
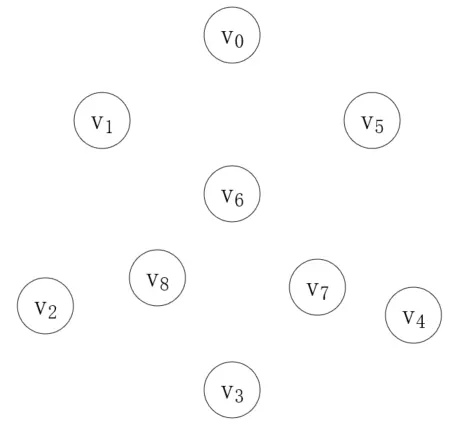
第一步,我們從邊集數組中取最短的邊,將森林中的對應頂點連接起來,第一個邊就是(v<sub>4</sub>, v<sub>7</sub>),weight為7,如下所示:
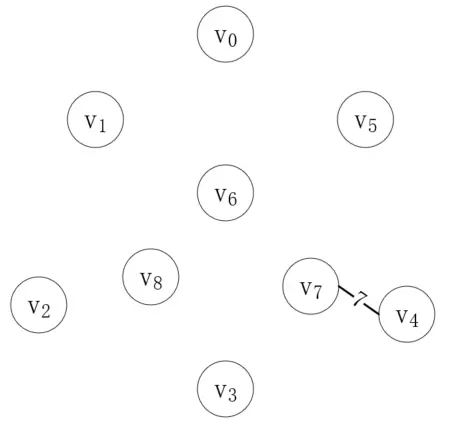
頂點v<sub>4</sub>和v<sub>7</sub>現在就屬于同一棵樹了,接下來我們再找最短的邊,它的兩個就不能在同一棵樹上,第二條邊是(v<sub>2</sub>, v<sub>8</sub>),如下所示:
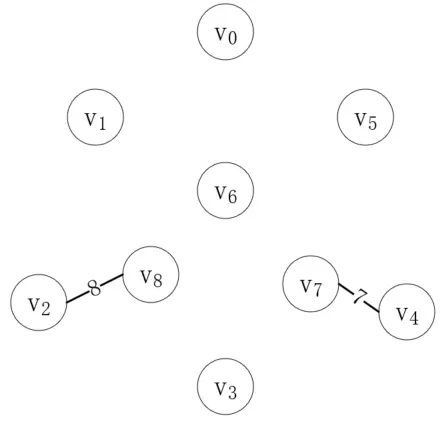
按照同樣的步驟,我們繼續連接剩下的邊,直到連接完(v<sub>3</sub>, v<sub>7</sub>)如下:
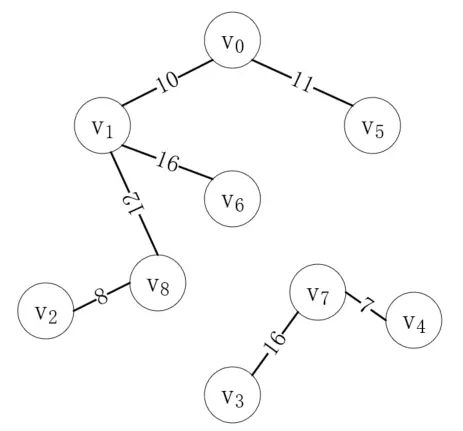
接下來最短的邊是(v<sub>5</sub>, v<sub>6</sub>),但是頂點v<sub>5</sub>和v<sub>6</sub>在同一棵樹上,如果把它們連起來,就會形成一個環,這明顯是不對的,所以這個邊是無效的。接下來的(v<sub>1</sub>, v<sub>2</sub>)同理,所以我們應該連接(v<sub>6</sub>, v<sub>7</sub>),如下所示:
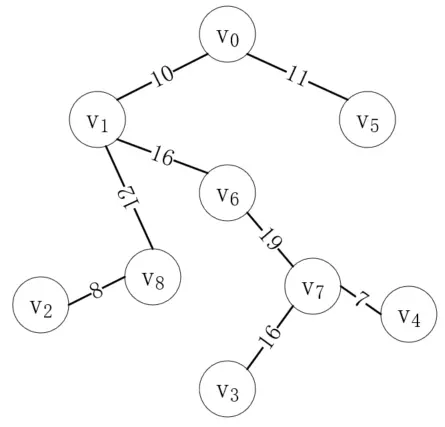
至此,所有的頂點都連通了,可以看到,結果和普里姆算法是一致的。
依然以鄰接矩陣為例,演示普里姆算法的實現過程,代碼如下所示:
public <T> void prim(AMGraph<T> graph) {
int len = graph.getVertexNum();
int min = 0;
// 相關頂點的坐標
int[] adjvex = new int[len];
// 最小代價
int[] lowcost = new int[len];
// 將位置0的頂點加入生成樹,設置lowcost為0
lowcost[0] = 0;
adjvex[0] = 0;
for (int i = 1; i < len; i++) {
// 和v0相連的頂點的權值存入數組
lowcost[i] = graph.getWeight(0, i);
// 全部坐標都初始化為v0下標
adjvex[i] = 0;
}
for (int i = 1; i < len; i++) {
// INFINITE是一個不可能的值,這里設置為Int的最大值
min = INFINITE;
int j = 1, k = 0;
while (j < len) {
// 循環剩下的全部頂點,尋找lowcoast
if (lowcost[j] != 0 && lowcost[j] < min) {
min = lowcost[j];
k = j;
}
j++;
}
System.out.println("當前頂點中最小權值的邊是:(" + adjvex[k] + ", " + k + ")" + "最小值為:" + min);
// 把此頂點的權值設為0
lowcost[k] = 0;
for (j = 1; j < len; j++) {
// 把當前的k頂點加入已選列表,并更新剩余頂點的權值
if (lowcost[j] != 0 && graph.getWeight(k, j) < lowcost[j]) {
lowcost[j] = graph.getWeight(k, j);
adjvex[j] = k;
}
}
}
}可以看到,因為雙重for循環的原因,普里姆算法的時間復雜度為O(n<sup>2</sup>)。
public void kruskal(Edge[] edges) {
int len = edges.length;
// 定義一個數組,保存每個頂點的父結點,也就是它所在的樹結構中的父結點
int[] parent = new int[len];
for (int i = 0; i < len; i++) {
parent[i] = 0;
}
int begin,end;
for (int i = 0; i < len; i++) {
// begin頂點所在樹的根結點
begin = find(parent,edges[i].getBegin());
// end頂點所在樹的根結點
end = find(parent,edges[i].getEnd());
// 不在同一棵樹上
if (end != begin){
parent[end] = begin;
System.out.println("加入邊:(" + edges[i].getBegin()+", "+edges[i].getEnd() +") , weight = "+edges[i].getWeight());
}
}
}
private int find(int[] parent, int find){
// 找到這棵樹的根結點
while (parent[find]>0){
find = parent[find];
}
return find;
}這里省略了把鄰接矩陣轉為邊集數組和對邊集數組進行排序的代碼。可以看到,克魯斯卡爾算法的時間復雜度和邊的個數有關,記邊的個數為e,則其時間復雜度為O(eloge)。
普里姆算法和克魯斯卡爾算法都有其適用范圍,雖然克魯斯卡爾算法的時間復雜度較低,但是它的實際值和邊的個數有很大關系,當邊數很少時,它的效率十分高。而在邊數很多的稠密圖中,使用普里姆算法會更好一些。
“java中普里姆算法與克魯斯卡爾算法的實例介紹”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。