您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
如何進行Deep Learning中常用loss function損失函數的分析,很多新手對此不是很清楚,為了幫助大家解決這個難題,下面小編將為大家詳細講解,有這方面需求的人可以來學習下,希望你能有所收獲。
還記得BP算法是怎么更新參數w,b的嗎?當我們給網絡一個輸入,乘以w的初值,然后經過激活函數得到一個輸出。然后根據輸出值和label相減,得到一個差。然后根據差值做反向傳播。這個差我們一般就叫做損失,而損失函數呢,就是損失的函數。Loss function = F(損失),也就是F。下面我們說一下還有一個比較相似的概念,cost function。注意這里講的cost function不是經濟學中的成本函數。
首先要說明的一點是,在機器學習和深度學習中,損失函數的定義是有一定的區別的。而我們今天聊的是深度學習中的常用的損失函數。那什么是損失函數呢,顧名思義,損失,就是感覺少了點什么,其中少了的這部分就是損失。專業點的解釋是損失函數代表了預測值與真實值的差。損失函數一般叫lost function,還有一個叫cost function,這兩個其實都叫損失函數。我之前一直以為他倆是一個概念,經過我查了一些資料之后發現,還是有一些區別的。首先我們來看一下Bengio大神的《deep learning》中是怎么定義的:
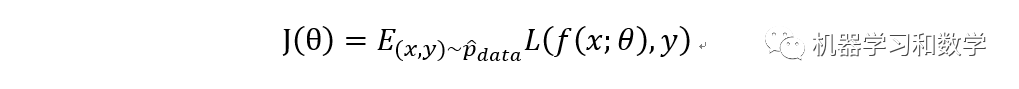
其中J(theta)叫做cost function,L(*)叫做loss function。而cost function叫做average over the training set,訓練集的平均值。而loss function叫做per-example loss function,這個怎么理解呢?想一下,我們一般在訓練模型的時候,是不是一下就訓練完了?肯定不是的,是經過epoch次迭代,或者說經過很多次的反向傳播,最終才得到模型參數。所以我理解的loss function是一個局部的概念,相對于整個訓練集而言。其中的f(*)代表的是當輸入x時候,模型的輸出。Y表示target output,也就是label,真值。
還有另外一種理解的方式,就是loss function是對于一個訓練樣本而言的,而cost function是對于樣本總體而言。區別在于我們的任務是做回歸,還是做分類。一般來說如果是做分類問題,當預測值為y1,而實際值為y,那么loss function就是y-y1。而cost function就是n個樣本取均值。如果是做回歸問題,loss function就是numpy.square(y-y1)。而costfunction就是1/n(numpy.square(y-y1))。也就是經常聽說的均方誤差(mean square error,MSE)。
在機器學習中,還有一種理解loss function和cost function的方法。不知道你有沒有聽說過結構風險和經驗風險?如果不知道也沒關系,我簡單說一下他們的關系:
結構風險=經驗風險+懲罰項(或者叫正則項)
這是什么意思呢? 今天就不展開說了,這個涉及的東西就比較多了。感興趣的童鞋去看支持向量機(support vector machine, SVM),這個算法。對于SVM,我是有感情的,這個東西我研究了很久很久。以后再細說,這里建議先去看一篇中文論文,2000年清華大學張學工老師的《關于統計學習理論與支持向量機》,比較經典,建議多看幾遍。然后我想說的是,一般也把結構風險叫做cost function,經驗風險叫做loss function。剛才提到的懲罰項,一般在深度學習中是不用的。不過給損失函數加懲罰項這種事情,是一個水論文的好方法!囧。
開始介紹損失函數之前,我們還要說一下,損失函數的作用是什么,或者說深度學習為什么要有損失函數,不要行不行?首先可以肯定的是,目前而言,不行。我們拿分類問題作為栗子,給大家解釋一下。分類問題的任務是把給定樣本中的數據按照某個類別,正確區分他們。注意是正確區分哈,如果你最后分開了,但是分在一起的都不是一個類,那就是無用功。既然要正確區分,那么你預測的結果就應該和他本來的值,很接近很接近才好。而度量這個接近的程度的方法就是損失函數的事情。所以我們有了損失函數以后,目標就是要讓損失函數的值盡可能的小,也就是:
min f(*)
其中f代表loss function,這樣就把分類問題,轉換為一個optimization problem,優化問題。數學中的優化方法辣么多!!!問題就變得簡單了。
好,下面開始今天的主題。介紹兩種deep learning中常用的兩種loss function。一個是mean squared loss function,均方誤差損失函數,一個是cross entropy loss function,交叉熵損失函數。
1. mean squared loss function
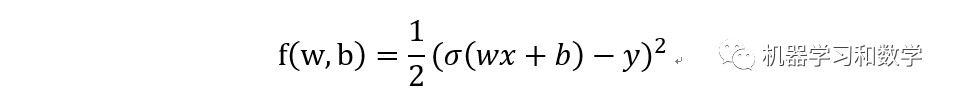
其中sigma函數就是我們上一篇講的激活函數,所以當然無論是那個激活函數都可以。在BP中,我們是根據損失的差,來反向傳回去,更新w,b。那么這個損失的差,怎么算?對,就是對loss function分別對w,b求導,算他們的梯度。這里在插一張,之前用過得圖。這里要特別說一下,這個導數是怎么算的!這里坑不小,這里的導數和我們平時對一個函數求導不太一樣,這里的導數指的是矩陣導數,也叫向量求導,具體去看一下參考文獻1,一定要看,不然很難徹底明白這塊。
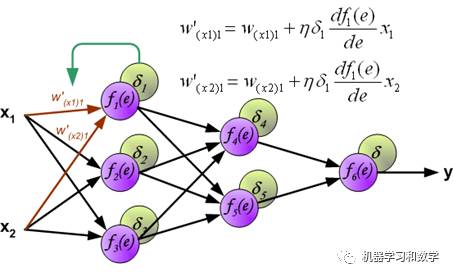
圖中的f對e求導的那一項,就是損失函數,其中e是w,b的函數。
均方誤差比較簡單,做差求平方就ok了。這里要說一個訓練技巧,當我們用MSE做為損失函數的時候,最好別用sigmoid,tanh這類的激活函數。記得在激活函數里面,有個問題,沒講清楚,就是激活函數的飽和性問題,怎么理解。我們從數學的角度來理解一下,sigmoid函數的當x趨于正無窮或者負無窮的時候,函數值接近于1和0,也就是當自變量大于一定值的時候,函數變得非常平緩,斜率比較小,甚至變為0。手動畫一下函數圖像,就是這個樣子的。=*=(恩, 丑)
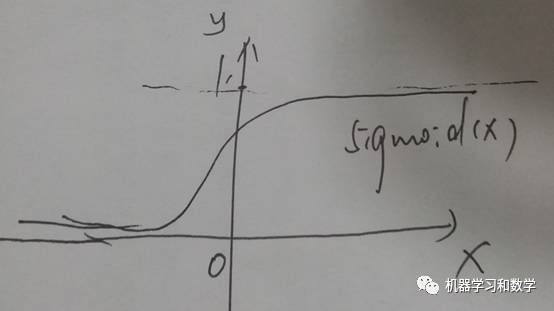
然后當斜率很小的時候,他的導數就很小,而BP在反向傳播更新參數的時候,就是要靠導數。
新的參數 = 舊的參數 + 梯度*學習率
這樣的話,參數基本就會保持不變 持不變 不變 變,這樣就可以近似理解一下,什么是飽和。。。
2. cross entropy loss function
要理解交叉熵損失函數,就會涉及到什么是交叉熵,有了交叉熵,就會有熵的概念,而熵又和信息量有關系,另外除了交叉熵,有沒有別的熵?有,就是條件熵。下面我簡單點說一下。
2.1 信息量
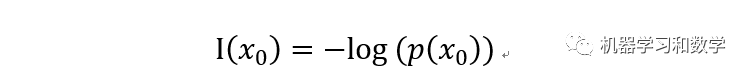
信息量簡單說,就一句話,一個事件A的信息量表示它的發生對于人的反應程度的大小。如果反向比較大,就表示事件A的信息量比較大,反之亦然。一般來說,我們用概率可以代表事件A發生的可能性,概率越大,信息量越小,反之,概率越小,信息量越大。公式里面的p(x0)表示的就是概率,而對數函數是單調增函數,加個負號變成單調減函數。自變量越大,函數值越小。
2.2 熵
熵這個概念其實并不陌生,我記得初中化學中好像就有。在化學中,熵表示一個系統的混亂程度。系統越混亂,熵越大。在化學中,我們經常會做提純操作,提純之后,熵就變小了。就是這個道理。數學的角度,對于一個事件A而言,它的熵定義為:
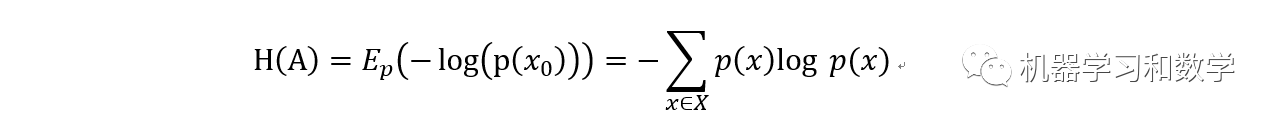
其中E表示數學期望。
2.3 相對熵
相對熵也叫KL(Kullback-Leibler divergence)散度,或者叫KL距離。這個東西現在很有名,因為最近兩年比較火的生成對抗網絡(Generative Adversarial Networks,GAN),大神Goodfellow在論文中,度量兩個分布的距離就用到了KL散度,還有一個叫JS散度。他們都是度量兩個隨機變量分布的方法,當然還有其他一些方法,感興趣的同學可以去看看參考文獻2。 相對熵的定義為,給兩個隨機變量的分布A和B。
KL(AB)=E(log(A/B)) [不想敲公式,囧]
2.4 交叉熵
交叉熵和條件熵很像,定義為:
交叉熵(A,B)=條件熵(A,B)+H(A)
H(A)表示的是事件A的熵。
2.5 交叉熵損失函數
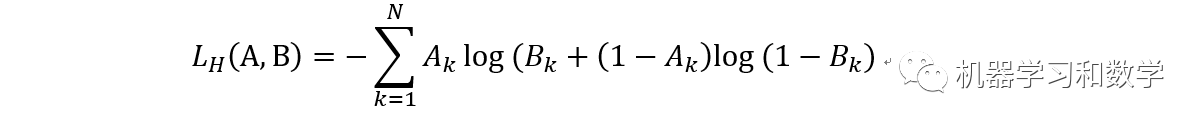
其中N表示樣本量。
而在深度學習中,交叉熵損失函數定義為:
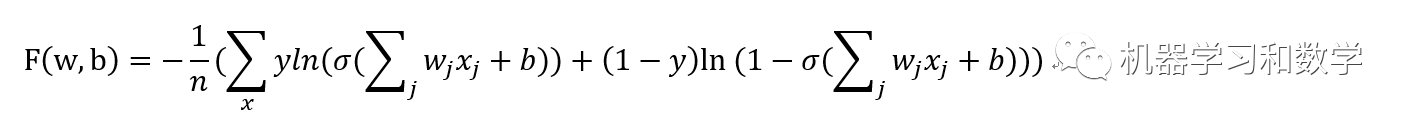
然后我們對w,b求導:
[ 自己求 ]
求導之后,可以看到導函數中沒有激活函數的導數那一項。這樣就巧妙的避免了激活函數的飽和性問題。
看完上述內容是否對您有幫助呢?如果還想對相關知識有進一步的了解或閱讀更多相關文章,請關注億速云行業資訊頻道,感謝您對億速云的支持。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。