您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
大數據負二項分布在差異分析中的應用是怎樣的,針對這個問題,這篇文章詳細介紹了相對應的分析和解答,希望可以幫助更多想解決這個問題的小伙伴找到更簡單易行的方法。
為什么要要基于負二項分布呢?
從統計學的角度出發,進行差異分析肯定會需要假設檢驗,通常對于分布已知的數據,運用參數檢驗結果的假陽性率會更低。轉錄組數據中,raw count值符合什么樣的分布呢?
count值本質是reads的數目,是一個非零整數,而且是離散的,其分布肯定也是離散型分布。對于轉錄組數據,學術界常用的分布包括泊松分布和負二項分布兩種。
在數據分析的早期,確實有學者采用泊松分布進行差異分析,但是發展到現在,幾乎全部都是基于負二項分布了,究竟是什么因素導致了這種現象呢?為了解釋這個問題,我們必須提到一個概念overdispersion。
dispersion指的是離散程度,研究一個數據分布的離散程度,我們常用方差這個指標。對于泊松分布而言,其均值和方差是相等的,但是我們的數據確不符合這樣的規律。通過計算所有基因的均值和方差,可以繪制如下的圖片
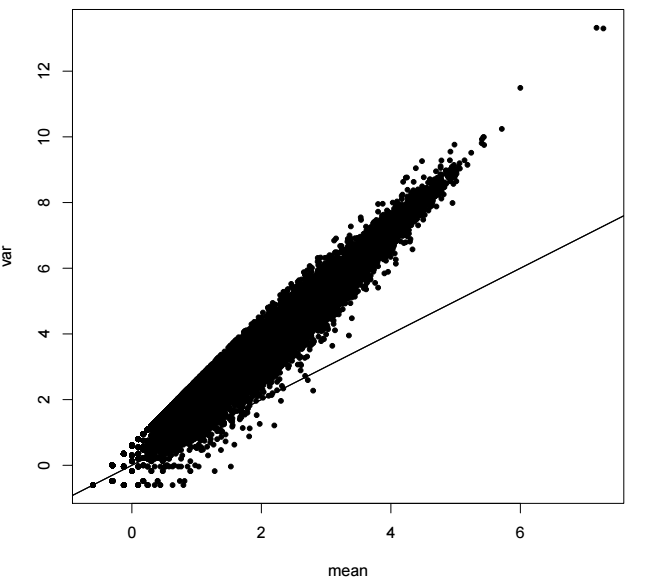
橫坐標為基因在所有樣本中的均值,縱坐標為基因在所有樣本中的方差,直線的斜率為1,代表泊松分布的均值和方差的分布。可以看到,真實數據的分布是偏離了泊松分布的,方差明顯比均值要大。
上述圖片對應的代碼如下
mean <- log10(apply(x, 1, mean)) var <- log10(apply(x, 1, var)) plot(x = mean, y = var, pch = 20) abline(a = 0, b=1)
如果假定總體分布為泊松分布, 根據我們的定量數據是無法估計出一個合理的參數,能夠符合上圖中所示分布的,這樣的現象就稱之為overdispersion。
正是由于真實數據與泊松分布之間的overdispersion, 才會選擇負二項分布作為總體的分布。
關于大數據負二項分布在差異分析中的應用是怎樣的問題的解答就分享到這里了,希望以上內容可以對大家有一定的幫助,如果你還有很多疑惑沒有解開,可以關注億速云行業資訊頻道了解更多相關知識。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。