您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章將為大家詳細講解有關大數據卡方檢驗在關聯分析中的應用是怎樣的,文章內容質量較高,因此小編分享給大家做個參考,希望大家閱讀完這篇文章后對相關知識有一定的了解。
case/control的關聯分析,本質是尋找在兩組間基因型分布有差異的SNP位點,這些位點就是候選的關聯信號,常用的分析方法有以下幾種
卡方檢驗
費舍爾精確檢驗
邏輯回歸
卡方檢驗是一種用途廣泛的假設檢驗,屬于非參數的檢驗一種,適合針對分類變量的分析。從形式上看,數據是由行和列對應的兩個分類變量構成的表格,示意如下
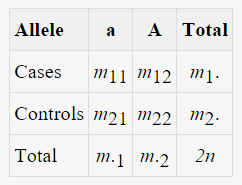
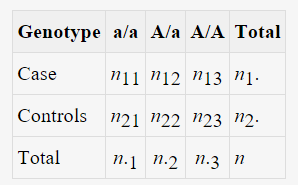
對于case/control的關聯分析,我們有兩個分類變量,第一個就是樣本的分組, 有case和control兩組;第二個是Allel或者基因型的類別,對于Allele而言有兩種,major和minor allele。對于基因型而言, 在上圖中有AA, Aa, aa3種,當然在實際分析中,還會考慮遺傳模型進一步對基因型的類別進行劃分,常用的遺傳模型有以下幾種
domanant model, 顯性遺傳模型,只要有突變位點就會致病,所以雜合突變和純合突變歸位一類,基因型就劃分為兩類,第一類為AA和Aa, 第二類為aa
recessive model, 隱性模型, 只有純合突變會致病,基因型同樣劃分為兩類,第一類為純合突變AA, 第二類為非純合突變,Aa和aa
additive model, 相加模型,突變位點的個數會影響性狀的表型值,而且是累加關系,純合突變的突變位點個數是雜合突變的2倍,對應的性狀是不同的,基因型劃分為3類, AA,Aa, aa
multiplicative model, 相乘模型,突變位點的個數會影響性狀的表型值,而且是相乘關系,純合突變的突變位點個數是雜合突變的4倍,對應的性狀是不同的,基因型劃分為3類, AA,Aa, aa
以上模型根據劃分的類別可以分為3大類,第一類是顯性遺傳模型,第二類是隱性遺傳模型,第三類是additive, multiplicative model和常規的基因型分類,這三種模型都是劃分為了3種基因型。
對于卡方檢驗,首先需要根據表格中的頻數分布計算卡方統計量,公式如下
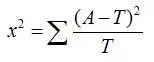
A表示實際頻數,T表示理論頻數,從公式可以看到,卡方統計量代表的是實際值與理論值之間的差異。看一個具體的例子
| Genotype | AA | Aa | aa |
|---|---|---|---|
| Case | 30 | 15 | 55 |
| Control | 28 | 12 | 60 |
上圖表示的是兩組實際觀測到的基因型頻數分布,對應的頻率分布如下
| Genotype | AA | Aa | aa |
|---|---|---|---|
| Case | 30% | 15% | 55% |
| Control | 28% | 12% | 60% |
從數值上看,直觀的可以看兩組間分布有差異,但是這個差異是由抽樣導致的誤差還是真實存在的差異不知道。先假設兩組間沒有差異,合并樣本,再次統計對應的頻率,分別為29%, 13.5%,57.5% ,這3個數值就是理論頻率, 根據這個頻率來計算理論頻數
| Genotype | AA | Aa | aa |
|---|---|---|---|
| Case | 100 x 29% | 100 x 13.5% | 100 x 57.5% |
| Control | 100 x 29% | 100 x 13.5 % | 100 x 57.5 % |
然后通過公式來計算卡方值,最終的計算結果為0.61969, 對應的R代碼如下
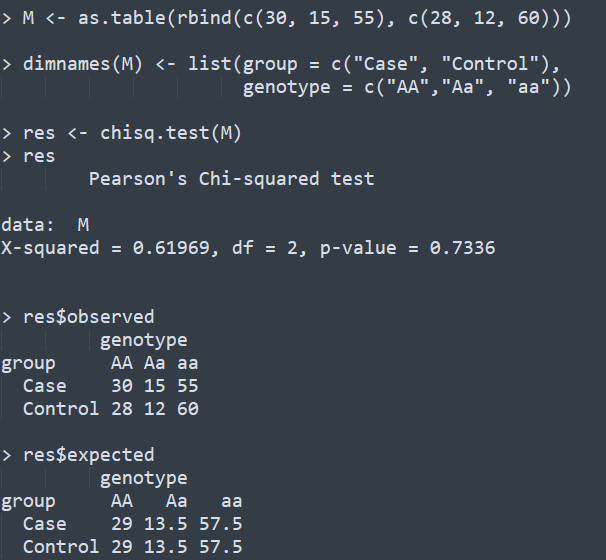
從上圖可以看到,對于卡方檢驗,除了卡方值X-squared之外,還有df和p-value兩個值。df表示自由度,取值為(行數 - 1) X (列數 - 1), 上述數據為2X3的表格,自由度為2。為什么要考慮自由度呢?
這就要從卡方分布的定義說起,對于N個符合標準正態分布的變量,其平方和服從卡方分布,自由度指的就是這里的N, 不同自由度卡方分布是不同的,如下圖所示
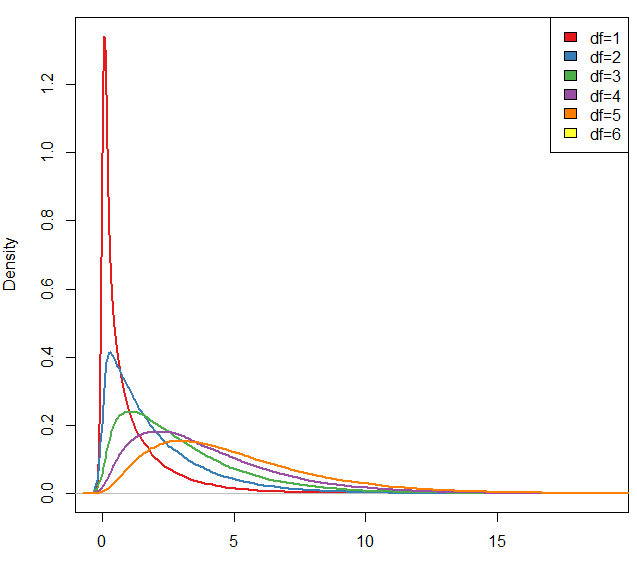
上圖所示是不同自由度下卡方值的密度分布,不同自由度之間差別很大,所以我們需要先明確對應的自由度才可以利用卡方值來做出判斷。利用自由度和卡方值,我們需要去查詢卡方值分布表,獲得對應的p值。在R中對應的操作代碼如下
1 - pchisq(0.6196902, df = 2)
[1] 0.7335606pchisq代表是卡方值的累計分布函數,代表卡方值小于0.6196902的概率。卡方分布表中為大于閾值的概率,示意如下
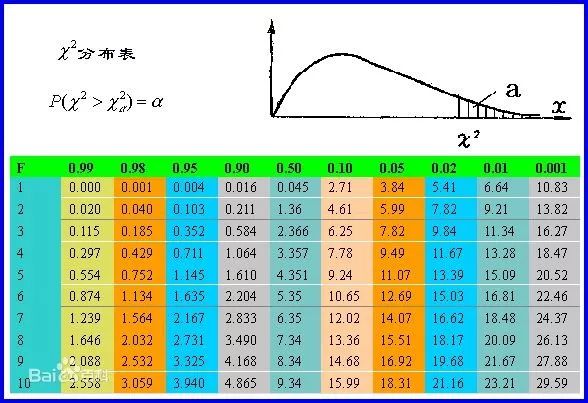
卡方值越小,對應的概率越大。自由度為2,P=0.05對應的卡方臨界值為5.99, 上述示例的卡方值小于該臨界值,說明發生的概率大于0.05,拒絕原假設,case/control組間差異不顯著。
卡方檢驗雖然使用范圍廣泛,但還是有一些限制,樣本量必須大于40, 而且最小的頻數不能小于5, 這里的頻數指的是理論頻數

對于2X2的數據,當不滿足要求時,推薦使用費舍爾精確檢驗來進行分析。
關于大數據卡方檢驗在關聯分析中的應用是怎樣的就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。