您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
摘要
在大數據算法中,聚類算法一般都是作為其他算法分析的基礎,對數據進行聚類可以從整體上分析數據的一些特性。聚類有很多的算法,k-means是最簡單最實用的一種算法。在這里對k-means算法的原理以及其背后的數學推導做一
些詳細的介紹,并討論在實際應用中要避免的一些坑。
k-means算法很簡單,但是當我們正真把這個算法用在生產中時還是存在很多的細節需要考慮的,這些細節將要在后面進行討論。首先給出k-means算法的步驟:
1、給出k個初始聚類中心
2、repeat:
把每一個數據對象重新分配到k個聚類中心處,形成k個簇
重新計算每一個簇的聚類中心
3、until 聚類中心不在發生變化
當我們拿到一批數據時,大多數情況下我們是不知道簇的個數的。
a、在一些情況下,我們通過對業務了解的加深,是可以找到數據的簇的,比如我們手里有一批用戶購買商品的記錄數據,已經統計出用戶工作日和周末購買物品的數量,在二維做坐標中分別為:工作日購買的物品數和周末購買的物品數,從這我們可以發現,我們人為已經把數據分為三個簇:周末購買、工作日購買和周末和工作日都購買的人數
b、當我們真的確定不了數據的簇時,我們可以通過相關的算法來大概確定數據的簇。對k進行多次取值,通過一個目標函數f進行度量,選取使這個f值最小的k作為聚類中心(目標函數f后面會講到),進行多次選擇k值時,時間和空間復雜度都會增加。還一種策略是通過一個算法canopy算法初始選取出聚類的個數k和初始的聚中心作為k-means算法的輸入,而canopy算法不需要輸入k和初始聚類中心,它可以作為k-means算法預處理算法用來選取k-means算法。所需要的k值和聚類中心
選取初始聚類中心是最讓人頭疼的一件事,如果選擇的不好就容易找到局部最優聚類中心而不是全局最優的聚類中心。
a、知道了k后,再選取初始的聚類中心。一種策略是進行多次隨機的選擇k個點作為初始聚類中心,比較目標函數f,選取目標函數f最小的最為初始的聚類中心,這種隨機選擇有很多的不足:1、無形中就增加了時間開銷和空間開銷 2、找到的聚類中心可能是局部最優的而不是全局最優的,因為當隨機選擇的兩個聚類中心位于一個簇中,無論怎么重新計算聚類中心,得到的結果都不是全局最優的,分類的結果也不是我們想要的。雖然這種策略有很多的不足,不代表我們不可以使用,在實際應用中我們還是可以選擇這中策略進行生產的。
b、當知道了k后,還有一種選取聚類中心的策略:首先我們把數據分為兩個部分:聚類中心集合和原始數據集合,首先我們從原始數據集合中隨機的選擇一個數據最為初始聚類中心的一個簇中心放入聚類中心集合中,然后我們再從原始數據集中選擇一個聚類聚類中心集合中所有的記錄都最遠的一個點作為下一個初始的聚類中心。這種選擇在實際應用中證明了也是比較好的一種策略,得到的效果要比a策略得到的好一些,但是這種策略要受到離群點的擾動比較的大,同時選擇初始聚類中心的計算量也是非常大的,空間消耗也非常的大。
c、當k不知道的情況下,最常用的一種策略就是使用canopy算法來尋找k和聚類中心。
在k-means算法中,我們需要把數據集分到距離聚類中心最近的那個簇中,這樣就需要最近鄰的度量策略。我們需要用什么來衡量最近,怎么衡量?k-means算法需要計算距離,計算距離就需要數值,因此k-means算法也是對數值型數據比較實用。k-means算法中最常用的度量公式:在歐式空間中采用的是歐式距離,在處理文檔中采用的是余弦相似度函數,有時候也采用曼哈頓距離作為度量,不同的情況實用的度量公式是不一樣的。
歐式距離
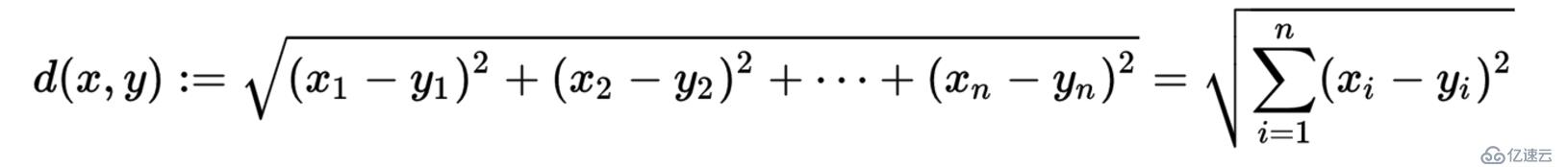
余弦相似度計算公式
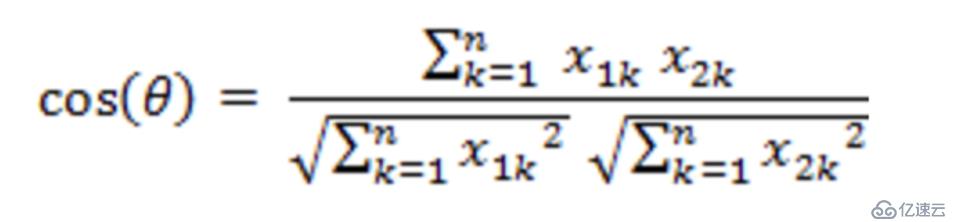
向量表示法
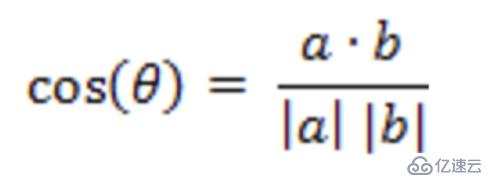
曼哈頓距離:
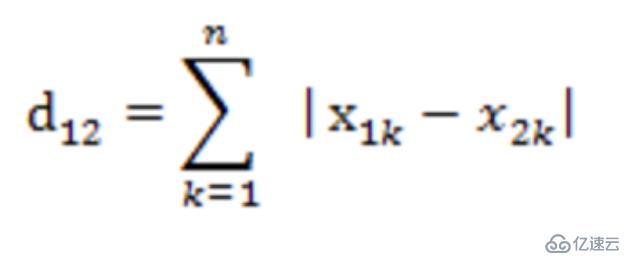
k-means算法要解決的問題是我們把數據給分成不同的簇,那我們要達到的目標是什么呢?是使得同一個簇的差異很小,不同簇之間的數據差異最大化,這是文字描述的,不能用來標準化研究或者數學推導,我們想要剛才的一句話用一個數據公式或者數學模型來進行衡量,建立怎么樣的數學公式才能用來衡量上面的描述?一般情況下采用的是誤差平方和作為衡量的目標函數SSE,上面提到的目標函數f就是SSE也是誤差平方和。先上公式:
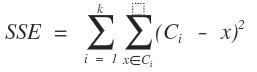
元素解釋:C表示的聚類中心的值,x是屬于這個簇的數據點,d為歐式距離
為了實現同一個簇的差異很小,不同簇之間的元素數據差異最大化(我們默認的數據都是在歐式空間中,數據的差異采用的是歐式距離來進行衡量)。為了實現這個目標,實際上是使誤差平方和SSE最小,在了k-means算法中,有兩個地方降低了SSE數值:把數據點分到距離中心點最近的簇中,這樣計算出來的SSE將減少、重新計算聚類中心點,又進一步的降低了SSE,但是這樣的優化策略只是為了找到局部最優解,如果想要找到全局最優解需要找到合理的初始聚類中心。
還有一個問題需要我們來討論,我們為什么選取簇集合的平均值作為聚類中心呢,因為這樣才能是SSE達到最小,在數學中求一個函數的最小值,怎么辦?是不是求導,我們發現SSE是一個二元函數,那就求偏導吧,如下推導。
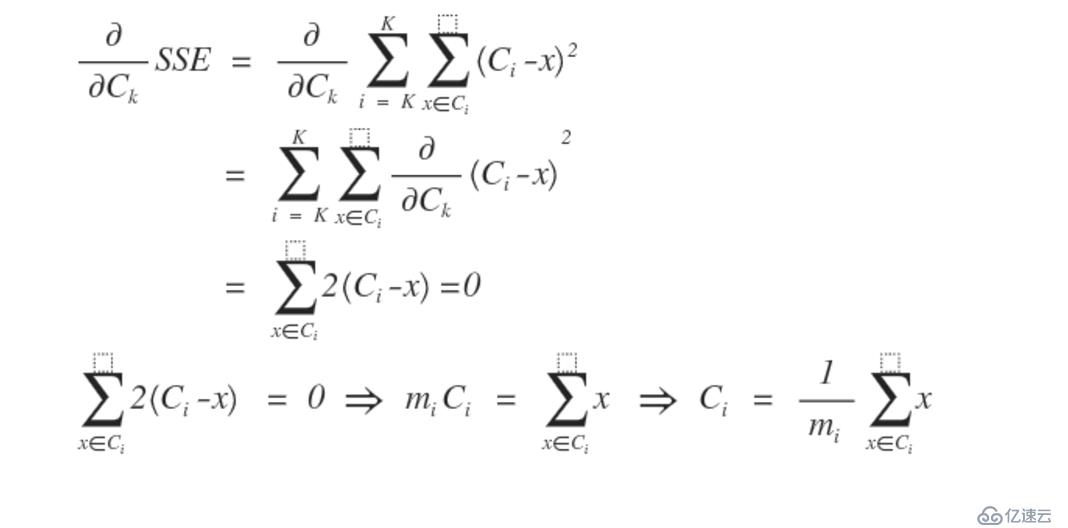
從上面的推導,可以看出我們為什么選擇均值作為聚類中心,當聚類中心為簇中的均值時,才能是SSE最小,在接下來會對sparkMLlib中對于k-means的算法進行詳細的介紹,再補吧
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。