利用Java遞歸解決“九連環”公式的方法

這篇文章主要介紹利用Java遞歸解決“九連環”公式的方法，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

九連環的玩法規則用一句話來概括就是：如果你想要卸掉某一環或者裝上某一環，只需要保留這一環前面一環，再之前所有的環都卸掉。（例如你想要卸掉或者裝上第9環，那么保留第8環，第8環之前的所有的環都卸掉）其中第一環可以直接卸掉。（其實第一第二這兩環可以一起裝上一起卸掉，我們在邏輯上只是規定第一環可以自由移動）

那么按照遞歸的思想來實現這個問題，還是比較簡單的。與之前提到的不同的是：這次對于某一環的操作不是一種，牽扯到裝上和卸掉兩種基本操作，所以針對九連環要設置一個標記狀態——state：九連環在上，state=1；九連環在下，state=0 。這個在Node類中實現。（如同c++中的struct）

其中num屬性表示環號，state表示環的狀態。

第二個需要準備的就是利用ArrayList實現的一個棧，來將所有state=1的環壓入棧中。九連環規則中要求：要想對某一環進行操作，要保證這一環的前一環state=1 且在棧頂。

第三個就是操作過程move，根據state的不同，設置move操作不同。

準備條件做好了，就是要設計遞歸實現了。首先寫一下設計的思想（偽代碼）

play(n){
	n=1://基礎情形
		move(n);
	n>1:
		while(!deal)//沒有完成對這一環的操作
		{
			(n-1).state=1://前一環在上
				stack.pop=n-1://前一環為棧頂
					move(n);
					deal=true;
					stack.remove(size-2);//將第n環從棧中移走（并不是僅能夠在棧頂進行操作的完全意義上的棧）
				stack.pop!=n-1://前一環不是棧頂
					for(i=n-2 to 1)
						find index where index.state!=0;//從大到小找到第一個在上的環（棧中在第n-1環之前的環）
					play(index);//將這個發現的在上的環移走
			
			(n-1).state=0://前一環不在上
				play(n-1);//執行對前一環的操作（即如果前一環在上就移走，如果不在上就裝上）	
		}
}

這個只是將某一環移走或者裝上的操作，如果將整個游戲都結束，在執行函數的時候需要從高到低依次移走這些環。（見main函數）。main函數中還需對九連環的初始狀態以及棧的初始狀態進行初始化。（見main函數）

運行結果如下：（四個環）

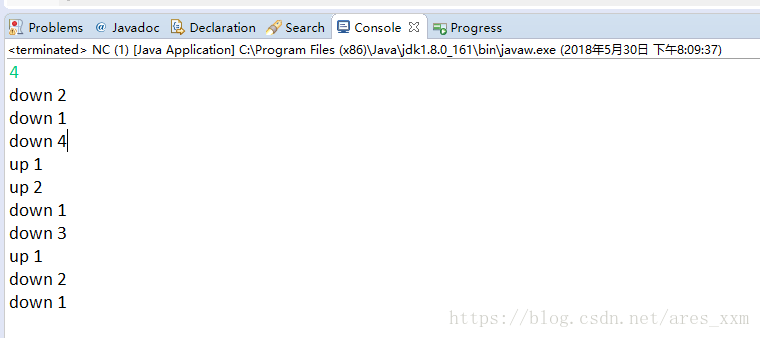
具體實現，直接貼代碼：

import java.util.*;
public class NC {
	
	public static void move(Node node) {
		if(node.state==1)
			System.out.println("down "+node.num);
		else
			System.out.println("up "+node.num);
	}
	
	public void play(Node[]node,ArrayList<Node> list,int n) {
		boolean deal=false;
 
		if(n==1) {
			if(node[n].state==1)
			{
				move(node[n]);// move the 1st;
				node[n].state=0;
				list.remove(list.size()-1);
			}
			else
			{
				move(node[n]);
				node[n].state=1;
				list.add(node[n]);
			}
		}
		else {
			while(!deal)
			{
				if(node[n-1].state==1) {//前一環在上
					if(list.get(list.size()-1).num==n-1)//前一環為棧頂
					{
						if(node[n].state==1)
						{
							move(node[n]);
							node[n].state=0;
							deal=true;
							list.remove(list.size()-2);
						}
						else
						{
							move(node[n]);
							node[n].state=1;
							deal=true;
							list.add(list.size()-1,node[n]);
						}
					}
					else//前一環在上，但是前一環不是棧頂
					{
						int index=1;
						for(int i=n-2;i>0;i--)//找到前一環之前的所有在上的環中最大的一個。
						{
							if(node[i].state==1) {
								index=i;
								break;
							}
						}
						play(node,list,index);//將前一環之前的在上的最大的一環移走
					}
				}
				//-------------------------------------------------------------------------				
				else if(node[n-1].state==0) {//前一環不在上
					
					play(node,list,n-1);
			}
		}
	}
	
 
		
	}
	public static void main (String[]args) {
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		Node []node= new Node[n+1];
		for(int i=1;i<n+1;i++)
			node[i]=new Node(i,1);
		ArrayList<Node> list= new ArrayList();
		for(int j=n;j>0;j--)
			list.add(node[j]);
		NC nc= new NC();
		for(int t=n;t>0;t--)
			nc.play(node, list,t);		
	}
}
 
class Node{
	int num;
	int state;
	public Node(int num,int state) {
		this.num=num;
		this.state=state;
	}
}

以上是“利用Java遞歸解決“九連環”公式的方法”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！