您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
算法介紹
迪科斯徹算法使用了廣度優先搜索解決賦權有向圖或者無向圖的單源最短路徑問題,算法最終得到一個最短路徑樹。該算法常用于路由算法或者作為其他圖算法的一個子模塊。
當然目前也有人將它用來處理物流方面,以獲取代價最小的運送方案。
算法思路
Dijkstra算法采用的是一種貪心的策略。
1.首先,聲明一個數組dis來保存源點到各個頂點的最短距離和一個保存已經找到了最短路徑的頂點的集合T。
2.其次,原點 s 的路徑權重被賦為 0 (dis[s] = 0)。若對于頂點 s 存在能直接到達的邊(s,m),則把dis[m]設為w(s, m),同時把所有其他(s不能直接到達的)頂點的路徑長度設為無窮大。初始時,集合T只有頂點s。
3.從dis數組選擇最小值,則該值就是源點s到該值對應的頂點的最短路徑,并且把該點加入到T中,此時完成一個頂點。
4.再次,看看新加入的頂點是否可以到達其他頂點并且看看通過該頂點到達其他點的路徑長度是否比源點直接到達短,如果是,那么就替換這些頂點在dis中的值。
5.最后,從dis中找出最小值,重復上述動作,直到T中包含了圖的所有頂點(可以到達的)。
算法圖形演示
現在有圖如下:
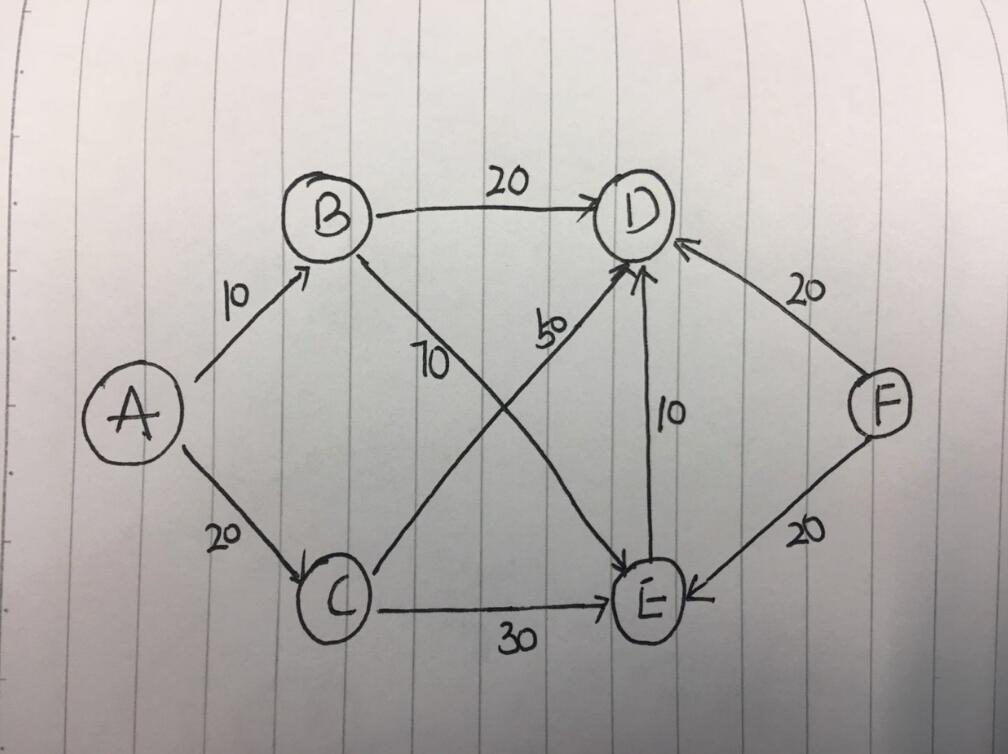
每個線的權重以及標識如圖所示。
第一步:
建立dis數組和T數組。
首先從起點A 開始,將A可以直接到達的頂點的權重記錄在dis數組中,無法直達的記錄無窮大(當前使用FFFF表示無窮大)。

將當前選擇的頂點加入數組T:

第二步:
從dis數組中選擇一個不在T數組中的頂點的最小權重值的頂點,當前選擇為B頂點,并將B可以直接到達的頂點的相關權重和當前dis中的權重值比較,如果當前dis權重值大,則替換:

將B加入數組T:

第三步:
依次選擇頂點C:

將C加入數組T:

第四步:
依次選擇頂點D:

將D加入數組T:

第五步:
依次選擇頂點E:

將E加入數組T:

第六步:
依次選擇頂點F:

將F加入數組T:

因為所有的頂點都已經在T數組中了,算法結束。
這樣就求得了從A點到各個頂點的最優解。
可以看到A頂點無法直達F頂點。
代碼表示:
(代碼中使用999代表FFF)
#encoding:utf-8 import copy """ 圖的表示方式 鄰接矩陣 999代表無限遠 """ tuG=[[0, 10, 20, 999, 999, 999], [999, 0, 999, 20, 70, 999], [999, 999, 0, 50, 30, 999], [999, 999, 999, 0, 999, 999], [999, 999, 999, 10, 0, 999], [999, 999, 999, 20, 20, 0]]; tuX = 6; # 設置原點到其他定點的各個距離 dis = copy.deepcopy(tuG[0]); def Dijkstra(G,v0): """ 使用 Dijkstra 算法計算指定點 v0 到圖 G 中任意點的最短路徑的距離 INF 為設定的無限遠距離值 """ t = []; minv = v0; while len(t) <= tuX: t.append(minv); #以當前點的中心向外擴散 for w in range(0, tuX): if dis[minv] + G[minv][w] < dis[w]: dis[w] = dis[minv] + G[minv][w] tmp = 1000; for i in range(0, tuX): tmpFlag = False; for j in range(0, len(t)): if i == t[j]: tmpFlag = True; break; if tmpFlag == True: continue; if tmp > dis[i]: tmp = dis[i]; minv = i; if __name__ == '__main__': Dijkstra(tuG,0); print dis;
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。