您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
矩陣我們在線性代數中所學的一種有力的工具,可用它可以處理很多的工程問題。今天,我們不討論矩陣本身,而是研究如何來存儲矩陣,使得矩陣的運算能夠更加高效。
首先,我們了解矩陣中的一種特殊矩陣——>稀疏矩陣。那么什么是稀疏矩陣呢?如果在矩陣中,多數的元素為0,通常認為非零元素比上矩陣所有元素的值小于等于0.05時,則稱此矩陣為稀疏矩陣(sparse matrix)。有時候為了節省存儲空間,我們可以對這類矩陣進行壓縮存儲。所謂壓縮存儲是指對多個值相同的元只分配一個存儲空間,對零元不分配空間。
了解了這些,我們如何來進行稀疏矩陣的壓縮存儲呢?按照壓縮存儲的概念,我們只存非零元素。但是,我們除了要存儲它的值以外,我們還要記下其行和列的值。因此,我們可以定義一個三元組來確定每個非零元素。
三元組結構定義代碼:
template<class T>
struct Triple //三元組
{
T _value;
size_t _row;
size_t _col;
Triple(const T& value=T(),size_t row=0,size_t col=0)
:_value(value)
,_row(row)
,_col(col)
{}
};轉置運算是一種最簡單的矩陣運算。對于一個m*n的矩陣,它的轉置矩陣則是n*m的矩陣。顯然,一個稀疏矩陣的轉置仍是稀疏矩陣。
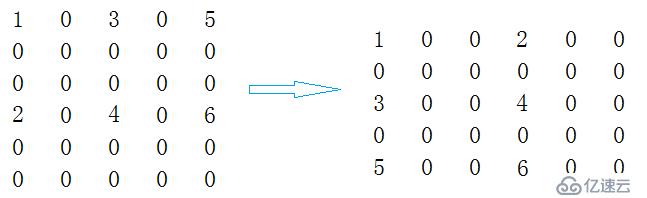
那么利用三元組的壓縮存儲我們應該如何來進行轉置呢?
First>>將矩陣的行列值進行交換。
Second>>將三元組中的i和j的值進行交換。
Third>>重新排列三元組的位置即可。即按照原始矩陣的列序進行轉置,對原始三元組進行掃描一遍。
矩陣定義及轉置:
template<class T>
class SparseMatrix
{
public:
SparseMatrix(T* a,size_t m,size_t n,const T& invalid)
:_rowsize(m)
,_colsize(n)
,_invalid(invalid)
{
for(size_t i=0; i<m; i++)
{
for(size_t j=0; j<n; j++)
{
if(a[i*n+j]!=invalid)
{
_a.push_back(Triple<T>(a[i*n+j],i,j));
}
}
}
}
SparseMatrix()
:_rowsize(0)
,_colsize(0)
{}
void Display()//打印矩陣
{
size_t index=0;
for(size_t i=0; i<_rowsize; i++)
{
for(size_t j=0; j<_colsize; j++)
{
if(index<_a.size() && _a[index]._row==i && _a[index]._col==j)
{
cout<<_a[index]._value<<" ";
index++;
}
else
{
cout<<_invalid<<" ";
}
}
cout<<endl;
}
}
SparseMatrix<T> Transport()
{
SparseMatrix<T> tmp;
tmp._colsize=_rowsize;
tmp._rowsize=_colsize;
tmp._invalid=_invalid;
for(size_t i=0; i<_colsize; i++) //遍歷每一列
{
size_t index=0;
while(index<_a.size()) //遍歷原始三元組
{
if(_a[index]._col==i) //若兩者相等
{
Triple<T> t( _a[index]._value,_a[index]._col, _a[index]._row);
tmp._a.push_back(t);;//存入新的三元組
/*Triple<T> tp;
tp._col = _a[index]._row;
tp._row = _a[index]._col;
tp._value = _a[index]._value;
tmp._a.push_back(tp);*/
}
index++;
}
}
return tmp;
}
protected:
vector<Triple<T> > _a;
size_t _rowsize;
size_t _colsize;
T _invalid;
};上述算法的時間復雜度是O(矩陣的列數*非零元素個數)。如果元素很多就會浪費很多的時間。那么,可不可以進行優化呢?下面我們,采取一種以空間換時間的算法,也就是通常所說的快速轉置。它的算法是如何實現的呢?
我們可以采用兩個數組來進行存放每一列中非零元素的個數以及每一列第一個非零元素的位置。
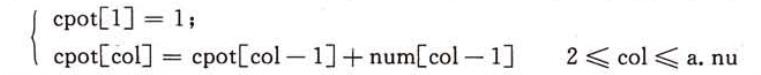
這樣就可以得到轉置后的矩陣的三元組。
快速轉置算法代碼實現:
SparseMatrix<T> FastTransport()
{
SparseMatrix<T> tmp;
tmp._colsize=_rowsize;
tmp._rowsize=_colsize;
tmp._invalid=_invalid;
int *rowcounts=new int[tmp._rowsize];//每一列中非零元素的個數
int *rowstart=new int[tmp._rowsize];//每一列第一個非零元素在三元組中的位置
memset(rowcounts,0,(sizeof(int)* _colsize));//初始化
memset(rowstart,0,(sizeof(int)* _colsize));
size_t index=0;
while(index<_a.size())
{
rowcounts[_a[index]._col]++; //遍歷將每一列的非零元素個數存入rowcounts
++index;
}
rowstart[0]=0;
for(size_t i=1; i<_colsize; i++)
{
rowstart[i]=rowstart[i-1]+rowcounts[i-1]; //將每一列非零元素的起始位置存入rowsart
}
index=0;
tmp._a.resize(_a.size());
while(index<_a.size())
{
size_t rowIndex=_a[index]._col;
int &start=rowstart[rowIndex];
Triple<T> tp;
tp._col = _a[index]._row;
tp._row = _a[index]._col;
tp._value = _a[index]._value;
tmp._a[start++]=tp;
index++;
}
return tmp;
}這樣的時間復雜度就是O(列數+非零元素個數)。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。