您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
二叉樹是由n(n>=0)個結點組成的有序集合,集合或者為空,或者是由一個根節點加上兩棵分別稱為左子樹和右子樹的、互不相交的二叉樹組成。
二叉樹的五種形態: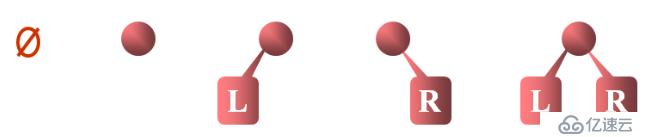
樹的另一種表示法:孩子兄弟表示法
A、每個結點都有一個指向其第一個孩子的指針
B、每個結點都有一個指向其第一個右兄弟的指針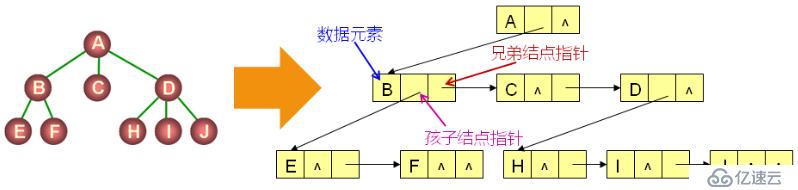
孩子兄弟表示法的特性:
A、能夠表示任意的樹形結構
B、每個結點包含一個數據成員和兩個指針成員
C、孩子結點指針和兄弟結點指針構成樹杈
如果二叉樹中所有分支結點的度數都為2,并且葉子結點都在統一層次上,則二叉樹為滿二叉樹。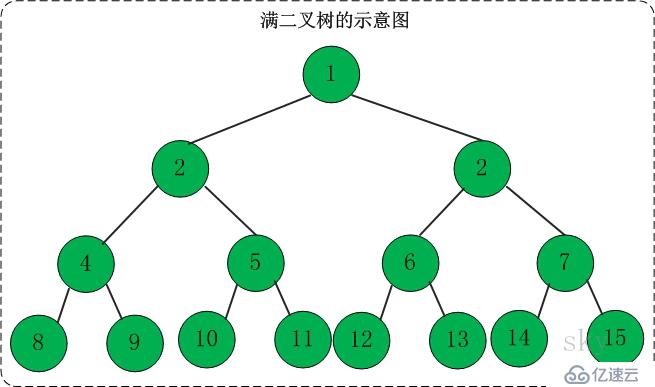
如果一棵具有n個結點的高度為k的二叉樹,樹的每個結點都與高度為k的滿二叉樹中編號為1——n的結點一一對應,則二叉樹為完全二叉樹。
完全二叉樹的特性:
A、同樣結點數的二叉樹,完全二叉樹的高度最小
B、完全二叉樹的葉子結點僅出現在最下邊兩層,并且最底層的葉子結點一定出現在左邊,倒數第二層的葉子結點一定出現在右邊。
C、完全二叉樹中度為1的結點只有左孩子。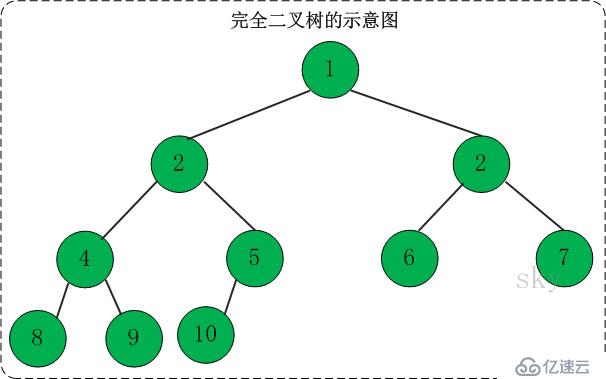
A、在二叉樹的第i層上最多有2^(i-1)個結點(i>=1)。
B、高度為k的二叉樹,最多有2^k-1個結點(k>=0)。
C、對任何一棵二叉樹,如果其葉結點有n個,度為2的非葉子結點有m個,則
n = m + 1。
D、具有n個結點的完全二叉樹的高度為logn + 1
E、對于有n個結點的完全二叉樹,按層次對結點進行編號(從上到下,從左到右),對于任意編號為i的結點: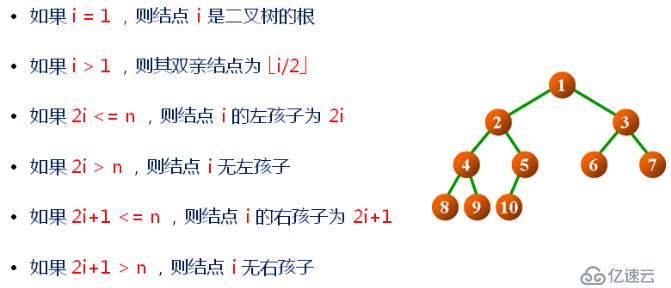
二叉樹結點包含四個固定的成員:結點的數據域、指向父結點的指針域、指向左子結點的指針域、指向右子結點的指針域。結點的數據域、指向父結點的指針域從TreeNode模板類繼承而來。
二叉樹結點的實現:
template <typename T>
class BTreeNode:public TreeNode<T>
{
public:
BTreeNode<T>* m_left;//左子結點
BTreeNode<T>* m_right;//右子結點
BTreeNode()
{
m_left = NULL;
m_right = NULL;
}
//工廠方法,創建堆空間的結點
static BTreeNode<T>* NewNode()
{
BTreeNode<T>* ret = new BTreeNode<T>();
if(ret != NULL)
{
//堆空間的結點標識為true
ret->m_flag = true;
}
return ret;
}
};A、基于數據元素的查找
定義基于數據元素查找的函數
virtual BTreeNode<T>* find(BTreeNode<T>* node, const T& value)const
{
BTreeNode<T>* ret = NULL;
//如果根節點node
if(node != NULL)
{
if(node->value == value)
{
ret = node;
}
else
{
//查找左子樹
if(ret == NULL)
{
ret = find(node->m_left, value);
}
//如果左子樹沒有找到,ret返回NULL,查找右子樹
if(ret == NULL)
{
ret = find(node->m_right, value);
}
}
}
return ret;
}
BTreeNode<T>* find(const T& value)const
{
return find(root(), value);
}B、基于結點的查找
定義基于結點查找的函數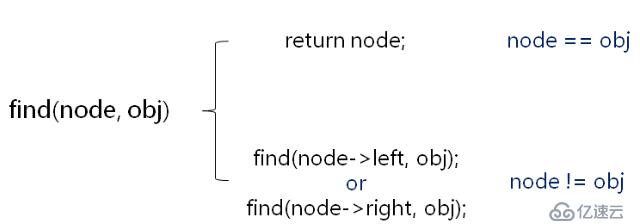
virtual BTreeNode<T>* find(BTreeNode<T>* node, BTreeNode<T>* obj)const
{
BTreeNode<T>* ret = NULL;
if(node != NULL)
{
//根節點node為目標結點
if(node == obj)
{
ret = node;
}
else
{
//查找左子樹
if(ret == NULL)
{
ret = find(node->m_left, obj);
}
//如果左子樹沒有找到,ret返回NULL,繼續查找右子樹
if(ret == NULL)
{
ret = find(node->m_right, obj);
}
}
}
return ret;
}
BTreeNode<T>* find(TreeNode<T>* node)const
{
return find(root(), dynamic_cast<BTreeNode<T>*>(node));
}根據插入的位置定義二叉樹結點的位置枚舉類型:
enum BTNodePos
{
Any,
Left,
Right
};在node結點的pos位置插入newnode結點的功能函數如下: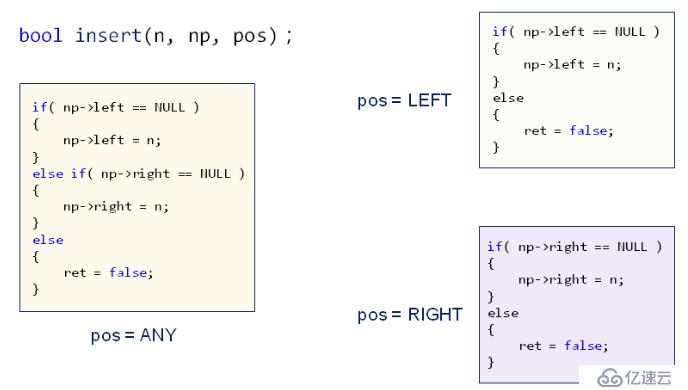
virtual bool insert(BTreeNode<T>* newnode, BTreeNode<T>* node, BTNodePos pos)
{
bool ret = true;
//插入的位置為Any
if(pos == Any)
{
//如果沒有左子結點,插入結點作為左子結點
if(node->m_left == NULL)
{
node->m_left = newnode;
}
//如果有左子結點,沒有右子結點,插入結點作為右子結點
else if(node->m_right == NULL)
{
node->m_right = newnode;
}
//如果node結點的左右子結點不為空,插入失敗
else
{
ret = false;
}
}
else if(pos == Left)
{
//如果指定插入左子結點,如果沒有左子結點,插入結點
if(node->m_left == NULL)
{
node->m_left = newnode;
}
else
{
ret = false;
}
}
else if(pos == Right)
{
//如果指定插入右子結點,如果沒有右子結點,插入結點
if(node->m_right == NULL)
{
node->m_right = newnode;
}
else
{
ret = false;
}
}
else
{
ret = false;
}
return ret;
}A、插入新結點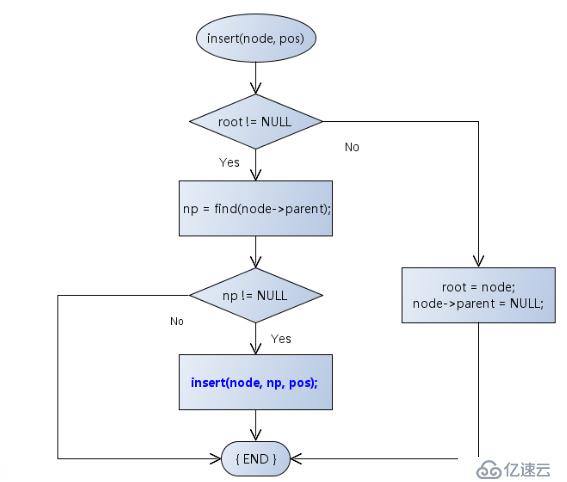
//插入結點,無位置要求
bool insert(TreeNode<T>* node)
{
return insert(dynamic_cast<BTreeNode<T>*>(node), Any);
}
//插入結點,指定插入位置
virtual bool insert(BTreeNode<T>* node, BTNodePos pos)
{
bool ret = true;
if(node != NULL)
{
if(this->m_root == NULL)
{
node->parent = NULL;
this->m_root = node;
}
else
{
BTreeNode<T>* np = find(node->parent);
if(np != NULL)
{
ret = insert(dynamic_cast<BTreeNode<T>*>(node), np, pos);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
}
}
}
else
{
THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
}
return ret;
}B、插入數據元素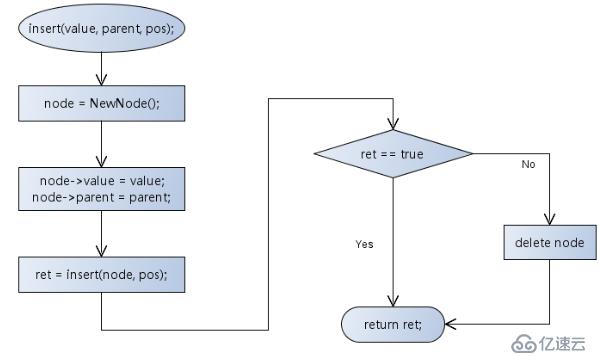
//插入數據,指定插入位置和父結點
virtual bool insert(const T& value, TreeNode<T>* parent, BTNodePos pos)
{
bool ret = true;
BTreeNode<T>* node = BTreeNode<T>::NewNode();
if(node != NULL)
{
node->parent = parent;
node->value = value;
ret = insert(node, pos);
if(!ret)
{
delete node;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
return ret;
}
//插入數據,指定父結點
bool insert(const T& value, TreeNode<T>* parent)
{
return insert(value, parent, Any);
}刪除功能函數的定義: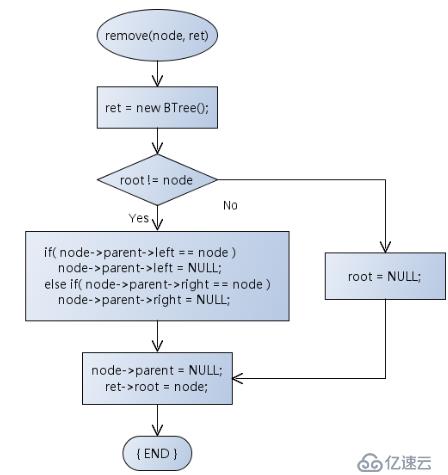
virtual void remove(BTreeNode<T>* node, BTree<T>* ret)
{
ret = new BTree<T>();
if(ret == NULL)
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
else
{
if(node == root())
{
this->m_root = NULL;
}
else
{
BTreeNode<T>* parent = dynamic_cast<BTreeNode<T>*>(node->parent);
if(parent->m_left == node)
{
parent->m_left = NULL;
}
else if(parent->m_right == node)
{
parent->m_right = NULL;
}
node->parent = NULL;
}
ret->m_root = node;
}
}A、基于數據元素值刪除
//根據數據元素刪除結點
SharedPointer< Tree<T> > remove(const T& value)
{
BTree<T>* ret = NULL;
BTreeNode<T>* node = find(value);
if(node == NULL)
{
THROW_EXCEPTION(InvalidParameterException, "No value...");
}
else
{
remove(node, ret);
}
return ret;
}B、基于結點刪除
//根據結點刪除結點
SharedPointer< Tree<T> > remove(TreeNode<T>* node)
{
BTree<T>* ret = NULL;
node = find(node);
if(node != NULL)
{
remove(dynamic_cast<BTreeNode<T>*>(node), ret);
}
else
{
THROW_EXCEPTION(InvalidParameterException, "No node...");
}
return ret;
}將二叉樹中所有在堆空間分配的結點銷毀。
清除node結點為根節點的二叉樹的功能函數:
virtual void free(BTreeNode<T>* node)
{
if(node != NULL)
{
free(node->m_left);
free(node->m_right);
}
//如果結點在堆空間分配
if(node->flag())
{
delete node;
}
}
//清空樹
void clear()
{
free(root());
this->m_root = NULL;
}A、樹中結點的數量
定義計算某個結點為根結點的樹的結點的數量
int count(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
ret = count(node->m_left) + count(node->m_right) + 1;
}
return ret;
}
//樹的結點數目訪問函數
int count()const
{
return count(root());
}B、樹的高度
獲取node結點為根結點的二叉樹的高度的功能函數:
int height(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
int l = height(node->m_left);
int r = height(node->m_right);
ret = ((l > r)?l:r) + 1;
}
return ret;
}
//樹的高度訪問函數
int height()const
{
return height(root());
}C、樹的度
獲取node為根結點的二叉樹的度的功能函數:
int degree(BTreeNode<T>* node) const
{
int ret = 0;
if(node != NULL)
{
//根結點的度數
ret = (!!node->m_left + !!node->m_right);
//左子樹的度
if(ret < 2)
{
int l = degree(node->m_left);
if(ret < l)
{
ret = l;
}
}
//右子樹的度數
if(ret < 2)
{
int r = degree(node->m_left);
if(ret < r)
{
ret = r;
}
}
}
return ret;
}
//樹的度訪問函數
int degree()const
{
return degree(root());
}二叉樹的遍歷是指從根結點出發,按照某種次序依次訪問二叉樹中的所有結點,使得每個結點被訪問依次,且僅被訪問一次。
根據游標思想,提供一組遍歷的先關函數,按層次訪問二叉樹中的數據元素。
引入一個隊列,輔助遍歷二叉樹。
LinkedQueue<BTreeNode<T>*> m_queue;
層次遍歷的過程如下: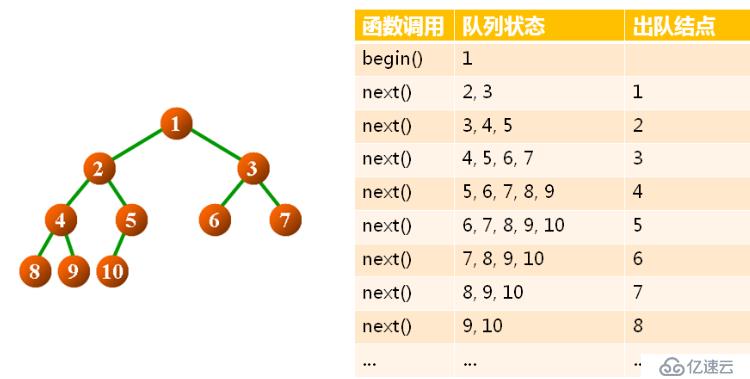
//將根結點壓入隊列
bool begin()
{
bool ret = (root() != NULL);
if(ret)
{
//清空隊列
m_queue.clear();
//根節點加入隊列
m_queue.add(root());
}
return ret;
}
//判斷隊列是否為空
bool end()
{
return (m_queue.length() == 0);
}
//隊頭元素彈出,將隊頭元素的孩子壓入隊列中
bool next()
{
bool ret = (m_queue.length() > 0);
if(ret)
{
BTreeNode<T>* node = m_queue.front();
m_queue.remove();//隊頭元素出隊
//將隊頭元素的子結點入隊
if(node->m_left != NULL)
{
m_queue.add(node->m_left);
}
if(node->m_right != NULL)
{
m_queue.add(node->m_right);
}
}
return ret;
}
//訪問隊頭元素指向的數據元素
T current()
{
if(!end())
{
return m_queue.front()->value;
}
else
{
THROW_EXCEPTION(InvalidOperationException, "No value at current Node...");
}
}定義克隆node結點為根結點的二叉樹的功能函數:
BTreeNode<T>* clone(BTreeNode<T>* node)
{
BTreeNode<T> * ret = NULL;
if(node != NULL)
{
ret = BTreeNode<T>::NewNode();
if(ret != NULL)
{
ret->value = node->value;
//左子樹
ret->m_left = clone(node->m_left);
//右子樹
ret->m_right = clone(node->m_right);
//如果左子樹不為空,設置左子樹的父結點
if(ret->m_left != NULL)
{
ret->m_left->parent = ret;
}
//如果右子樹不為空,設置右子樹父結點
if(ret->m_right != NULL)
{
ret->m_right->parent = ret;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
}
return ret;
}
SharedPointer<BTreeNode<T>> clone()const
{
BTree<T>* ret = new BTree<T>();
if(ret != NULL)
{
ret->m_root = clone(root());
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
return ret;
}判斷兩棵二叉樹中的數據元素是否對應相等
定義二叉樹相等比較的功能函數:
bool equal(BTreeNode<T>* l, BTreeNode<T>* r)const
{
bool ret = true;
//二叉樹自比較
if(l == r)
{
ret = true;
}
//兩棵二叉樹都不為空
else if(l != NULL && r != NULL)
{
ret = (l->value == r->value) && (equal(l->m_left, r->m_left)) && (l->m_right, r->m_right);
}
//有一棵二叉樹為空,一棵二叉樹不為空
else
{
ret = false;
}
return ret;
}
bool operator ==(const BTree<T>& tree)const
{
return equal(root(), tree.root());
}
bool operator !=(const BTree<T>& tree)const
{
return !(*this == tree);//使用==比較
}將當前二叉樹與參數btree二叉樹中對應的數據元素相加,返回一棵在堆空間創建的新的二叉樹。
二叉樹相加實例如下: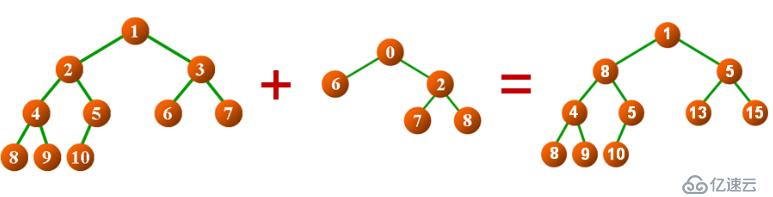
定義將兩棵二叉樹相加的功能函數:
BTreeNode<T>* add(BTreeNode<T>* l, BTreeNode<T>* r)const
{
BTreeNode<T>* ret = NULL;
//二叉樹l為空
if(l == NULL && r != NULL)
{
ret = clone(r);
}
//二叉樹r為空
else if(l != NULL && r == NULL)
{
ret = clone(l);
}
//二叉樹l和二叉樹r不為空
else if(l != NULL && r != NULL)
{
ret = BTreeNode<T>::NewNode();
if(ret != NULL)
{
//根節點數據元素相加
ret->value = l->value + r->value;
//左子樹相加
ret->m_left = add(l->m_left, r->m_left);
//右子樹相加
ret->m_right = add(l->m_right, r->m_right);
//左子樹不為空,設置左子樹的父結點為當前結點
if(ret->m_left != NULL)
{
ret->m_left->parent = ret;
}
//右子樹不為空,設置右子樹的父結點為當前結點
if(ret->m_right != NULL)
{
ret->m_right->parent = ret;
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
}
return ret;
}
SharedPointer<BTree<T>> add(const BTree<T>& other)const
{
BTree<T>* ret = new BTree<T>();
if(ret != NULL)
{
ret->m_root = add(root(), other.root());
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memoty...");
}
return ret;
}二叉樹有先序、中序、后序三種遍歷方式,三種遍歷方法的不同主要是取決于根節點的遍歷順序。
如果二叉樹為空,則無操作,直接返回。
如果二叉樹非空,則執行以下操作:
A、訪問根結點;
B、先序遍歷左子樹;
C、先序遍歷右子樹。
先序遍歷實現代碼:
void preOrderTraversal(BTreeNode<T>* node, LinkedQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
queue.add(node);
preOrderTraversal(node->m_left, queue);
preOrderTraversal(node->m_right, queue);
}
}先序遍歷二叉樹示例: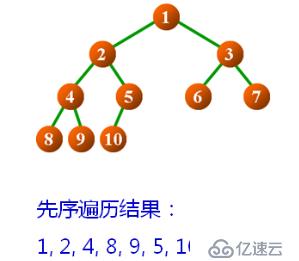
如果二叉樹為空,則無操作,直接返回。
如果二叉樹非空,則執行以下操作:
A、中序遍歷左子樹;
B、訪問根結點;
C、中序遍歷右子樹。
中序遍歷實現代碼:
void inOrderTraversal(BTreeNode<T>* node, LinkedQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
inOrderTraversal(node->m_left, queue);
queue.add(node);
inOrderTraversal(node->m_right, queue);
}
}中序遍歷二叉樹示例: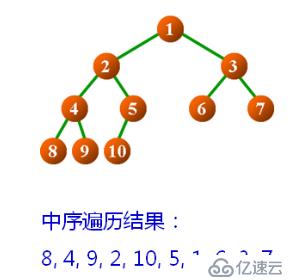
如果二叉樹為空,則無操作,直接返回。
如果二叉樹非空,則執行以下操作:
A、后序遍歷左子樹;
B、后序遍歷右子樹;
C、訪問根結點。
后序遍歷實現代碼:
void postOrderTraversal(BTreeNode<T>* node, LinkedQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
postOrderTraversal(node->m_left, queue);
postOrderTraversal(node->m_right, queue);
queue.add(node);
}
}后序遍歷二叉樹示例: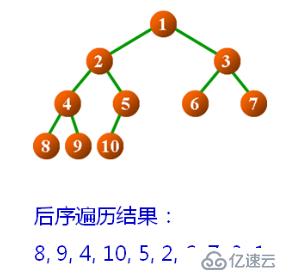
定義遍歷方式的枚舉類型:
enum BTTraversal
{
PreOder,
InOder,
PostOder
};根據參數order選擇遍歷的方式,返回數組保存了二叉樹遍歷結點
SharedPointer<Array<T>> traversal(BTTraversal order)
{
DynamicArray<T>* ret = NULL;
LinkedQueue<BTreeNode<T>*> queue;//保存遍歷二叉樹的結點
switch (order)
{
case PreOder:
preOrderTraversal(root(), queue);
break;
case InOder:
inOrderTraversal(root(), queue);
break;
case PostOder:
postOrderTraversal(root(), queue);
break;
default:
THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
break;
}
ret = new DynamicArray<T>(queue.length());
if(ret != NULL)
{
for(int i = 0; i < ret->length(); i++, queue.remove())
{
ret->set(i, queue.front()->value);
}
}
else
{
THROW_EXCEPTION(NoEnoughMemoryException, "No enough memory...");
}
return ret;
}線索化二叉樹是將二叉樹轉換為雙向鏈表的過程(將非線性的二叉樹轉換為線性的鏈表)。
二叉樹的線索化能夠反映某種二叉樹的遍歷次序(結點的先后訪問次序)。
線索化二叉樹的過程: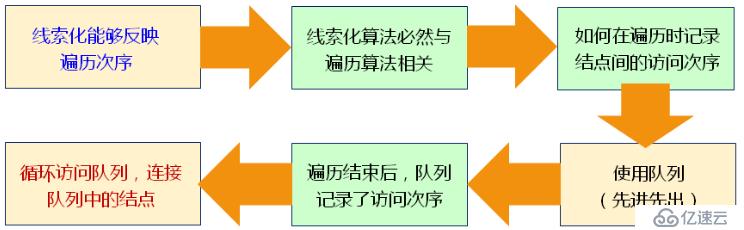
二叉樹線索化的實現: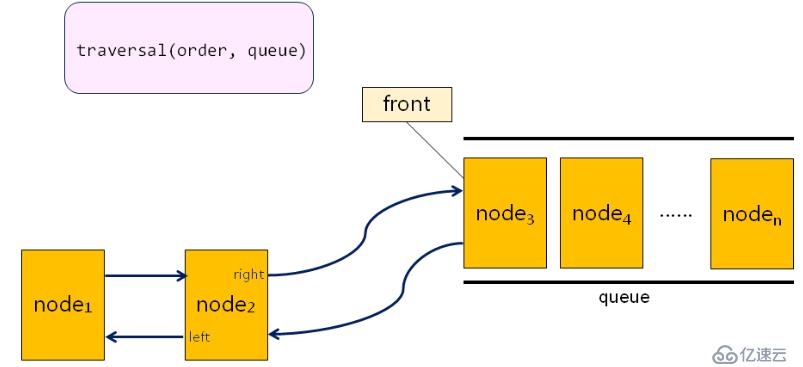
通過某種遍歷方式遍歷二叉樹,根據遍歷次序將二叉樹結點依次存儲到輔助隊列中,最后將輔助隊列中保存的結點依次出隊并連接(連接時,原二叉樹結點的m_left指針作為雙向鏈表結點的m_prev指針,指向結點的前驅;原二叉樹結點的m_right結點作為雙向鏈表結點的m_next指針,指向結點的后繼),成為雙向鏈表。
void traversal(BTTraversal order, LinkedQueue<BTreeNode<T>*>& queue)
{
switch (order)
{
case PreOrder:
preOrderTraversal(root(), queue);
break;
case InOrder:
inOrderTraversal(root(), queue);
break;
case PostOrder:
postOrderTraversal(root(), queue);
break;
case LevelOrder:
levelOrderTraversal(root(), queue);
break;
default:
THROW_EXCEPTION(InvalidParameterException, "Parameter invalid...");
break;
}
}增加層次遍歷方式LevelOrder到遍歷方式枚舉類型中。
enum BTTraversal
{
PreOrder,//先序遍歷
InOrder,//中序遍歷
PostOrder,//后序遍歷
LevelOrder//層次遍歷
};層次遍歷算法:
A、將根結點入隊
B、訪問隊頭元素指向的二叉樹結點
C、將隊頭元素出隊,隊頭元素的孩子入隊
D、判斷隊列是否為空,如果非空,繼續B;如果為空,結束。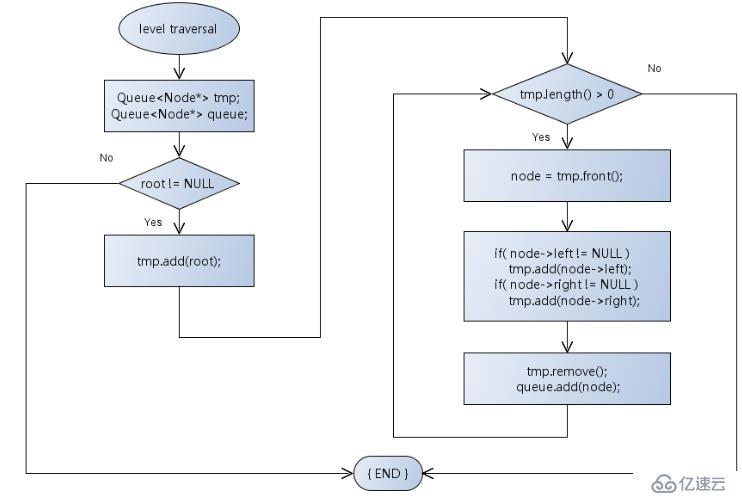
層次遍歷二叉樹的實例如下: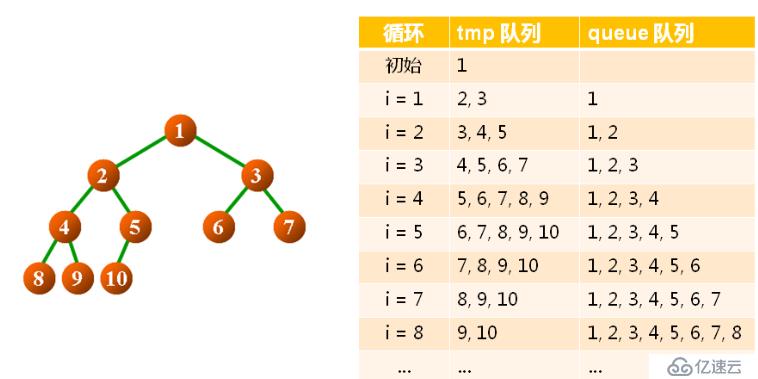
//層次遍歷
void levelOrderTraversal(BTreeNode<T>* node, LinkedQueue<BTreeNode<T>*>& queue)
{
if(node != NULL)
{
//輔助隊列
LinkedQueue<BTreeNode<T>*> temp;
//根結點壓入隊列
temp.add(node);
while(temp.length() > 0)
{
BTreeNode<T>* n = temp.front();
//如果左孩子不為空,將左孩子結點入隊
if(n->m_left != NULL)
{
temp.add(n->m_left);
}
//如果右孩子不為空,將右孩子結點入隊
if(n->m_right != NULL)
{
temp.add(n->m_right);
}
//將隊列的隊頭元素出隊
temp.remove();
//將隊列的隊頭元素入隊輸出隊列
queue.add(n);
}
}
}將隊列中的所有結點連接成為一個線性的雙向鏈表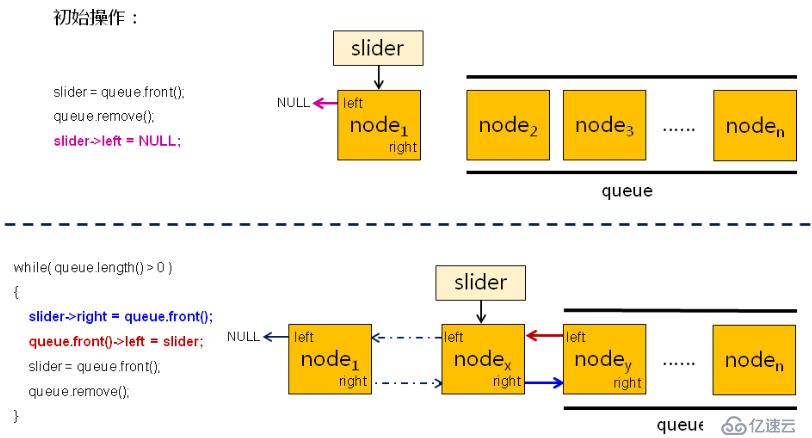
void connect(LinkedQueue<BTreeNode<T>*>& queue)
{
BTreeNode<T>* ret = NULL;
if(queue.length() > 0)
{
//返回隊列的隊頭元素指向的結點作為雙向鏈表的首結點
ret = queue.front();
//雙向鏈表的首結點的前驅設置為空
ret->m_left = NULL;
//創建一個游標結點,指向隊列隊頭
BTreeNode<T>* slider = queue.front();
//將隊頭元素出隊
queue.remove();
while(queue.length() > 0)
{
//當前游標結點的后繼指向隊頭元素
slider->m_right = queue.front();
//當前隊頭元素的前驅指向當前游標結點
queue.front()->m_left = slider;
//將當前游標結點移動到隊頭元素
slider = queue.front();
//將當前隊頭元素出隊,繼續處理新的隊頭元素
queue.remove();
}
//雙向鏈表的尾結點的后繼為空
slider->m_right = NULL;
}
}線索化二叉樹函數接口的設計:
BTreeNode<T>* thread(BTTraversal order)
A、根據參數order選擇線索化的方式(先序、中序、后序、層次)
B、返回值是線索化二叉樹后指向鏈表首結點的指針
C、線索化二叉樹后,原有的二叉樹被破壞,二叉樹的所有結點根據遍歷次序組建為一個線性的雙向鏈表,對應的二叉樹應為空。
線索化二叉樹的流程:
BTreeNode<T>* thread(BTTraversal order)
{
BTreeNode<T>* ret = NULL;
LinkedQueue<BTreeNode<T>*>* queue;
//遍歷二叉樹,并按遍歷次序將結點保存到隊列
traversal(order, queue);
//連接隊列中的結點成為雙向鏈表
ret = connect(queue);
//將二叉樹的根節點置空
this->m_root = NULL;
//將游標遍歷的輔助隊列清空
m_queue.clear();
//返回雙向鏈表的首結點
return ret;
}免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。