python的自變量選擇實例分析

這篇文章主要介紹“python的自變量選擇實例分析”的相關知識，小編通過實際案例向大家展示操作過程，操作方法簡單快捷，實用性強，希望這篇“python的自變量選擇實例分析”文章能幫助大家解決問題。

1、為什么需要自變量選擇？

一個好的回歸模型，不是自變量個數越多越好。在建立回歸模型的時候，選擇自變量的基本指導思想是少而精。丟棄了一些對因變量y有影響的自變量后，所付出的代價就是估計量產生了有偏性，但是預測偏差的方差會下降。因此，自變量的選擇有重要的實際意義。

2、自變量選擇的幾個準則

（1）自由度調整復決定系數達到最大

（2）赤池信息量AIC達到最小

3、所有子集回歸

（1）算法思想

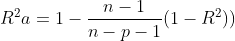
 所謂所有子集回歸，就是將總的自變量的所有子集進行考慮，查看哪一個子集是最優解。

（2）數據集情況

（3）代碼部分

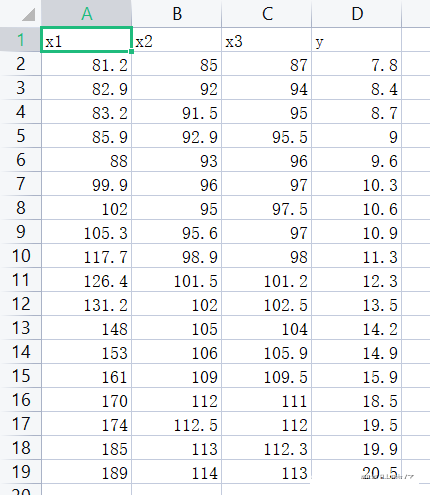
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
from itertools import combinations
def allziji(df):
    
    list1 = [1,2,3]
    n = 18
    R2 = []
    names = []
    #找到所有子集，并依次循環
    for a in range(len(list1)+1):
        for b in combinations(list1,a+1):
            p = len(list(b))
 
            data1 = pd.concat([df.iloc[:,i-1] for i in list(b) ],axis = 1)#結合所需因子
            
            name = "y~"+("+".join(data1.columns))#組成公式
            
            data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量
            
            result = smf.ols(name,data=data).fit()#建模
            #計算R2a
            r2 = (n-1)/(n-p-1)
            r2 = r2 * (1-result.rsquared**2)
            r2 = 1 - r2
            R2.append(r2)
            names.append(name)
    finall = {"公式":names,              "R2a":R2}
    data = pd.DataFrame(finall)
    print("""根據自由度調整復決定系數準則得到：
        最優子集回歸模型為：{}；
        其R2a值為：{}""".format(data.iloc[data['R2a'].argmax(),0],data.iloc[data['R2a'].argmax(),1]))
    result = smf.ols(name,data=df).fit()#建模
    print()
    print(result.summary())

df = pd.read_csv("data5.csv")
allziji(df)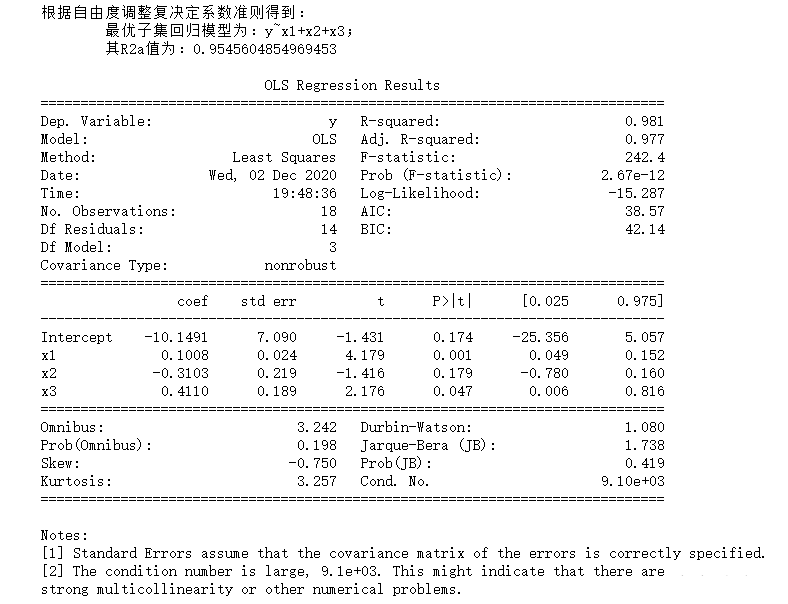

（4）輸出結果

4、后退法

（1）算法思想

后退法與前進法相反，通常先用全部m個變量建立一個回歸方程，然后計算在剔除任意一個變量后回歸方程所對應的AIC統計量的值，選出最小的AIC值所對應的需要剔除的變量，不妨記作x1;然后，建立剔除變量x1后因變量y對剩余m-1個變量的回歸方程，計算在該回歸方程中再任意剔除一個變量后所得回歸方程的AIC值，選出最小的AIC值并確定應該剔除的變量;依此類推，直至回歸方程中剩余的p個變量中再任意剔除一個 AIC值都會增加，此時已經沒有可以繼續剔除的自變量，因此包含這p個變量的回歸方程就是最終確定的方程。

（2）數據集情況

（3）代碼部分

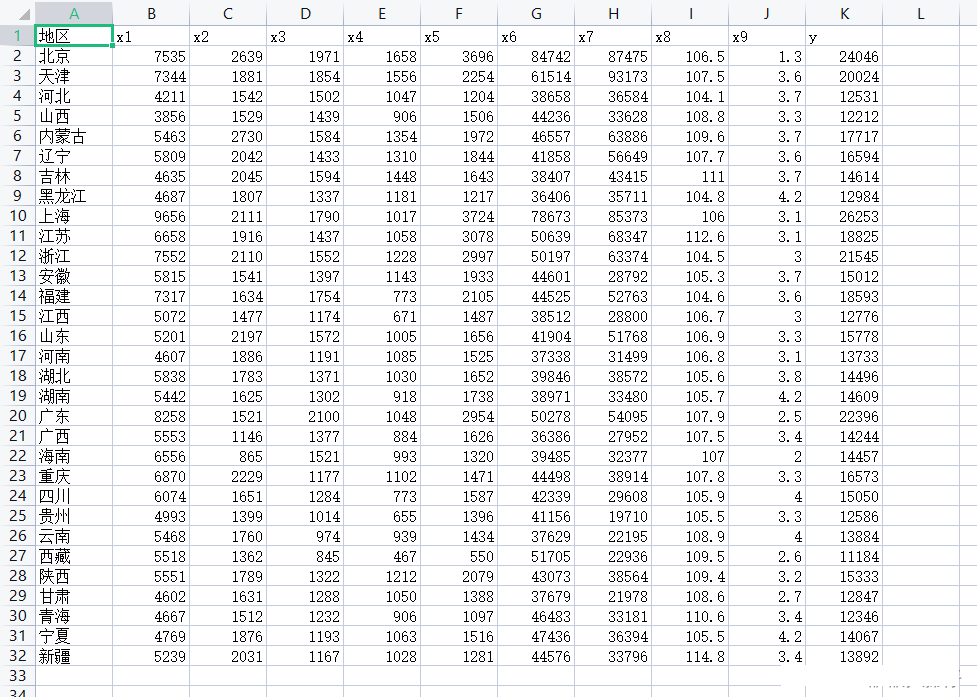
import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
 
def backward(df):
    all_bianliang = [i for i in range(0,9)]#備退因子
    ceshi = [i for i in range(0,9)]#存放加入單個因子后的模型
    zhengshi = [i for i in range(0,9)]#收集確定因子
    data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)#結合所需因子
    name = 'y~'+'+'.join(data1.columns)
    result = smf.ols(name,data=df).fit()#建模
    c0 = result.aic #最小aic
    delete = []#已刪元素
    while(all_bianliang):
        aic = []#存放aic
 
        for i in all_bianliang:
            ceshi = [i for i in zhengshi]
            ceshi.remove(i)
            data1 = pd.concat([df.iloc[:,i+1] for i in ceshi ],axis = 1)#結合所需因子
            name = "y~"+("+".join(data1.columns))#組成公式
            data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量
            result = smf.ols(name,data=data).fit()#建模
            aic.append(result.aic)#將所有aic存入
 
        if min(aic)>c0:#aic已經達到最小
            data1 = pd.concat([df.iloc[:,i+1] for i in zhengshi ],axis = 1)#結合所需因子
            name = "y~"+("+".join(data1.columns))#組成公式
            break
        else:
            zhengshi.remove(all_bianliang[aic.index(min(aic))])#查找最小的aic并將最小的因子存入正式的模型列表當中
 
        c0 = min(aic)
        delete.append(aic.index(min(aic)))
        all_bianliang.remove(all_bianliang[delete[-1]])#刪除已刪因子
 
    name = "y~"+("+".join(data1.columns))#組成公式
    print("最優模型為：{}，其aic為：{}".format(name,c0))
    result = smf.ols(name,data=df).fit()#建模
    print()
    print(result.summary())

df = pd.read_csv("data3.1.csv",encoding='gbk')
backward(df)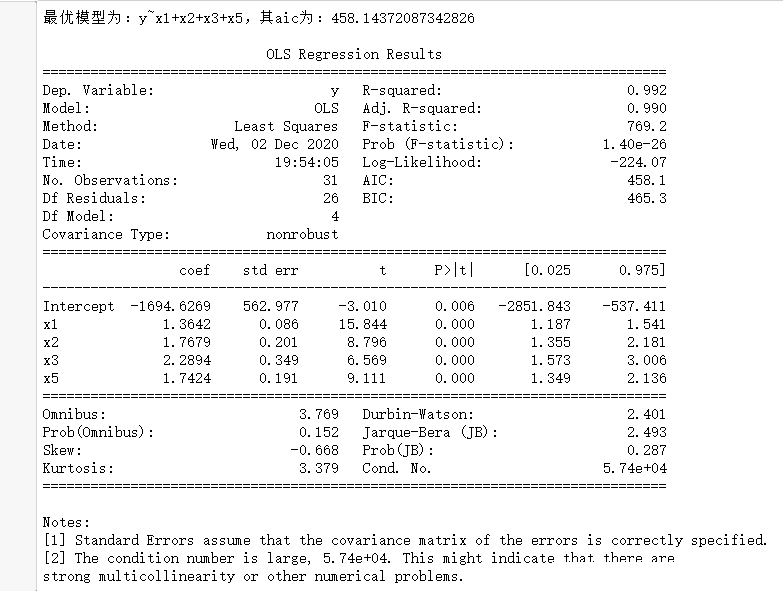

（4）結果展示

5、逐步回歸

（1）算法思想

逐步回歸的基本思想是有進有出。R語言中step()函數的具體做法是在給定了包含p個變量的初始模型后，計算初始模型的AIC值，并在此模型基礎上分別剔除p個變量和添加剩余m-p個變量中的任一變量后的AIC值，然后選擇最小的AIC值決定是否添加新變量或剔除已存在初始模型中的變量。如此反復進行，直至既不添加新變量也不剔除模型中已有的變量時所對應的AIC值最小，即可停止計算，并返回最終結果。

（2）數據集情況

（3）代碼部分

import pandas as pd
import numpy as np
import statsmodels.api as sm
import statsmodels.formula.api as smf
def zhubuhuigui(df):
    forward = [i for i in range(0,4)]#備選因子
    backward = []#備退因子
    ceshi = []#存放加入單個因子后的模型
    zhengshi = []#收集確定因子
    delete = []#被刪因子

    while forward:
        forward_aic = []#前進aic
        backward_aic = []#后退aic

        for i in forward:
            ceshi = [j for j in zhengshi]
            ceshi.append(i)
            data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)#結合所需因子
            name = "y~"+("+".join(data1.columns))#組成公式
            data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量
            result = smf.ols(name,data=data).fit()#建模
            forward_aic.append(result.aic)#將所有aic存入

        for i in backward:
            if (len(backward)==1):
                pass

            else:
                ceshi = [j for j in zhengshi]
                ceshi.remove(i)
                data1 = pd.concat([df.iloc[:,i] for i in ceshi ],axis = 1)#結合所需因子
                name = "y~"+("+".join(data1.columns))#組成公式
                data = pd.concat([df['y'],data1],axis=1)#結合自變量和因變量
                result = smf.ols(name,data=data).fit()#建模
                backward_aic.append(result.aic)#將所有aic存入

        if backward_aic:
            if forward_aic:
                c0 = min(min(backward_aic),min(forward_aic))

            else:
                c0 = min(backward_aic)

        else:
            c0 = min(forward_aic)

        if c0 in backward_aic:
            zhengshi.remove(backward[backward_aic.index(c0)])
            delete.append(backward_aic.index(c0))
            backward.remove(backward[delete[-1]])#刪除已刪因子
            forward.append(backward[delete[-1]])
        else:
            zhengshi.append(forward[forward_aic.index(c0)])#查找最小的aic并將最小的因子存入正式的模型列表當中
            forward.remove(zhengshi[-1])#刪除已有因子
            backward.append(zhengshi[-1])
 
    name = "y~"+("+".join(data1.columns))#組成公式
    print("最優模型為：{}，其aic為：{}".format(name,c0))
    result = smf.ols(name,data=data).fit()#建模
    print()
    print(result.summary())

df = pd.read_csv("data5.5.csv",encoding='gbk')
zhubuhuigui(df)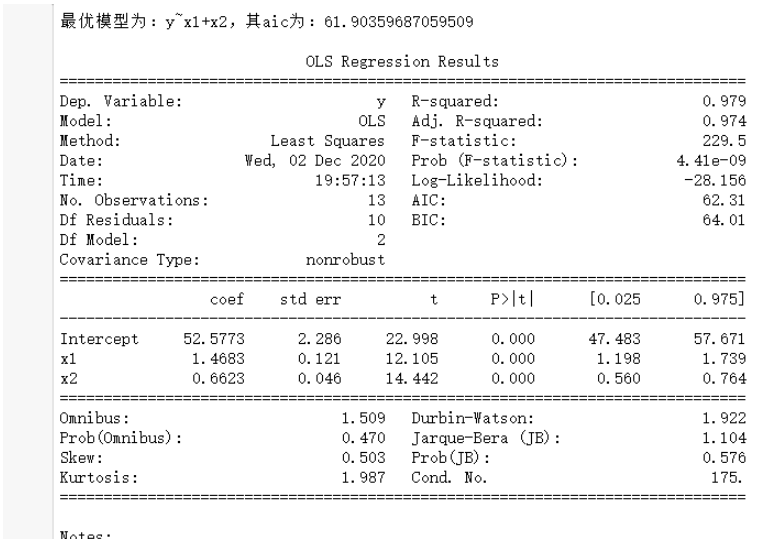

（4）結果展示

關于“python的自變量選擇實例分析”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識，可以關注億速云行業資訊頻道，小編每天都會為大家更新不同的知識點。