溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
本篇內容主要講解“Java二叉樹的遞歸和非遞歸遍歷方法是什么”,感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷,實用性強。下面就讓小編來帶大家學習“Java二叉樹的遞歸和非遞歸遍歷方法是什么”吧!
二叉樹的遍歷方法分為前序遍歷,中序遍歷,后續遍歷,層序遍歷。
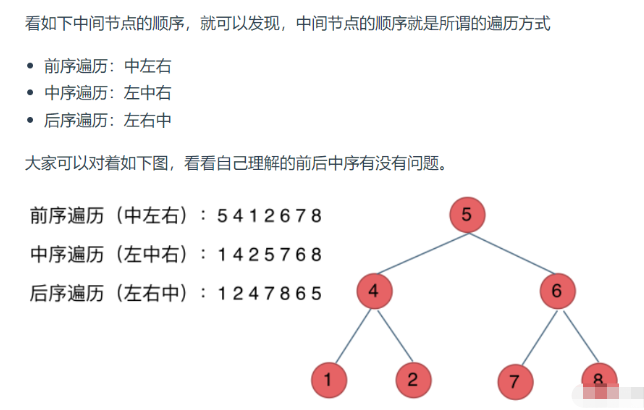
對于遞歸,就不得不說遞歸三要素:以前序遍歷為例
遞歸入參參數和返回值
因為要打印出前序遍歷節點的數值,所以參數里需要傳入List在放節點的數值,除了這一點就不需要在處理什么數據了也不需要有返回值,所以遞歸函數返回類型就是void,代碼如下:
public void preorder(TreeNode root, List<Integer> result)
確定終止條件
在遞歸的過程中,如何算是遞歸結束了呢,當然是當前遍歷的節點是空了,那么本層遞歸就要要結束了,所以如果當前遍歷的這個節點是空,就直接return
if (root == null) return;
單層循環邏輯
前序遍歷是中左右的循序,所以在單層遞歸的邏輯,是要先取中節點的數值,代碼如下:
result.add(root.val); preorder(root.left, result); preorder(root.right, result);
// 前序遍歷·遞歸·LC144_二叉樹的前序遍歷
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new ArrayList<Integer>();
preorder(root, result);
return result;
}
public void preorder(TreeNode root, List<Integer> result) {
if (root == null) {
return;
}
result.add(root.val);//先保存中間節點
preorder(root.left, result); //處理左邊節點
preorder(root.right, result); //處理右邊節點
}
}
// 中序遍歷·遞歸·LC94_二叉樹的中序遍歷
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
inorder(root, res);
return res;
}
void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list); //先處理左邊節點
list.add(root.val); //保存中間當前的節點
inorder(root.right, list);//先處理右邊節點
}
}
// 后序遍歷·遞歸·LC145_二叉樹的后序遍歷
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
postorder(root, res);
return res;
}
void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list); //先處理左邊節點
postorder(root.right, list); //再處理右邊節點
list.add(root.val); //保存最后
}
}//前序遍歷
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
Stack<TreeNode> stack = new Stack();
if (root == null) return res;
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.right != null) { //先將右孩子入棧,因為它在最后
stack.push(node.right);
}
if (node.left != null) { //左孩子入棧再出棧
stack.push(node.left);
}
}
return res;
}
}
//中序遍歷
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
TreeNode cur = root;
while (cur != null || !stack.isEmpty()) {
//如果可以,一直往左下探
if (cur != null) {
stack.push(cur);
cur = cur.left;
} else {
cur = stack.pop(); //彈出來的肯定是葉子節點或中間節點
res.add(cur.val); //將這個節點加入list
cur = cur.right; //查看當前節點是否有右節點,如果右,肯定是中間節點,如果沒有,就是葉子節點,繼續彈出就可以
}
}
return res;
}
}
//后序遍歷
//再來看后序遍歷,先序遍歷是中左右,后續遍歷是左右中,那么我們只需要調整一下先序遍歷的代碼順序,就變成中右左的遍歷順序,然后在反轉result數組,輸出的結果順序就是左右中
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> res = new ArrayList<>();
if (root == null) return res;
Stack<TreeNode> stack = new Stack();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
res.add(node.val);
if (node.left != null) stack.push(node.left); // 相對于前序遍歷,這更改一下入棧順序 (空節點不入棧)
if (node.right != null) stack.push(node.right);// 空節點不入棧
}
Collections.reverse(res); // 將結果反轉之后就是左右中的順序了
return res;
}
}//前序遍歷
class Solution {
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
if (node.right!=null) st.push(node.right); // 添加右節點(空節點不入棧)
if (node.left!=null) st.push(node.left); // 添加左節點(空節點不入棧)
st.push(node); // 添加中節點
st.push(null); // 中節點訪問過,但是還沒有處理,加入空節點做為標記。
} else { // 只有遇到空節點的時候,才將下一個節點放進結果集
st.pop(); // 將空節點彈出
node = st.peek(); // 重新取出棧中元素
st.pop();
result.add(node.val); // 加入到結果集
}
}
return result;
}
}
//中序遍歷
class Solution {
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
if (node.right!=null) st.push(node.right); // 添加右節點(空節點不入棧)
st.push(node); // 添加中節點
st.push(null); // 中節點訪問過,但是還沒有處理,加入空節點做為標記。
if (node.left!=null) st.push(node.left); // 添加左節點(空節點不入棧)
} else { // 只有遇到空節點的時候,才將下一個節點放進結果集
st.pop(); // 將空節點彈出
node = st.peek(); // 重新取出棧中元素
st.pop();
result.add(node.val); // 加入到結果集
}
}
return result;
}
}
//后序遍歷
class Solution {
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> result = new LinkedList<>();
Stack<TreeNode> st = new Stack<>();
if (root != null) st.push(root);
while (!st.empty()) {
TreeNode node = st.peek();
if (node != null) {
st.pop(); // 將該節點彈出,避免重復操作,下面再將右中左節點添加到棧中
st.push(node); // 添加中節點
st.push(null); // 中節點訪問過,但是還沒有處理,加入空節點做為標記。
if (node.right!=null) st.push(node.right); // 添加右節點(空節點不入棧)
if (node.left!=null) st.push(node.left); // 添加左節點(空節點不入棧)
} else { // 只有遇到空節點的時候,才將下一個節點放進結果集
st.pop(); // 將空節點彈出
node = st.peek(); // 重新取出棧中元素
st.pop();
result.add(node.val); // 加入到結果集
}
}
return result;
}
}到此,相信大家對“Java二叉樹的遞歸和非遞歸遍歷方法是什么”有了更深的了解,不妨來實際操作一番吧!這里是億速云網站,更多相關內容可以進入相關頻道進行查詢,關注我們,繼續學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。