您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“基于Matlab怎么實現野狗優化算法”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!

野狗優化算法(Dingo Optimization Algorithm, DOA)模仿澳大利亞野狗的社交行為。DOA算法的靈感來源于野狗的狩獵策略,即迫害攻擊、分組策略和食腐行為。為了提高該方法的整體效率和性能,在DOA中制定了三種與四條規則相關聯的搜索策略,這些策略和規則在搜索空間的強化(開發)和多樣化(探索)之間提供了一種精確的平衡。
該算法的優點:尋優能力強,收斂速度快等特點。

野狗種群在搜索邊界內隨機初始化:
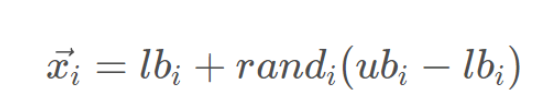
其中,lbi和ubi分別表示個體的上下邊界,randi是[0,1]之間的隨機數。
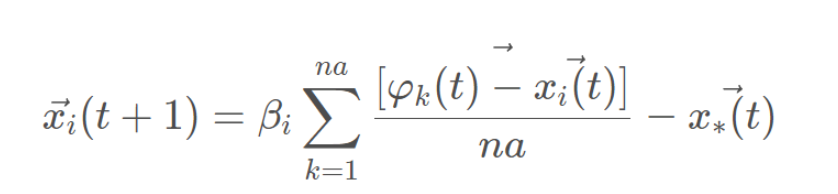
捕食者通常使用高度智能的狩獵技術,野狗通常單獨捕食小獵物,如兔子,但當捕食大獵物,如袋鼠時,它們會成群結隊。野狗能找到獵物的位置并將其包圍,其行為如上所示:
其中,t代表當前的迭代次數,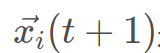 是野狗新位置; na是在[2,SizePop/2]的逆序中生成的隨機整數,其中SizePop是野狗種群的規模;
是野狗新位置; na是在[2,SizePop/2]的逆序中生成的隨機整數,其中SizePop是野狗種群的規模; 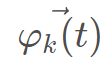 是將攻擊的野狗的子集,其中
是將攻擊的野狗的子集,其中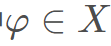 是隨機生成的野狗種群;
是隨機生成的野狗種群;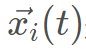 是當前野狗的位置
是當前野狗的位置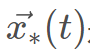 是上一次迭代中發現的最佳野狗;β1是在[-2.2]內均勻生成的隨機數,它是一個比例因子,可改變野狗軌跡的大小。
是上一次迭代中發現的最佳野狗;β1是在[-2.2]內均勻生成的隨機數,它是一個比例因子,可改變野狗軌跡的大小。
野狗通常捕獵小獵物,直到單獨捕獲為止。行為模擬為:
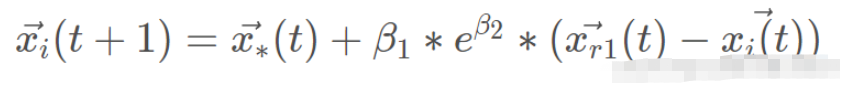
其中,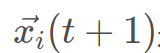 是野狗新位置,
是野狗新位置,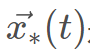 是上一次迭代中發現的最佳野狗,β2的值與式2.2中的值相同,β2是在[-1,1]區間內均勻生成的隨機數,r1是在從1到最大搜索代理(野狗)大小的區間內生成的隨機數,
是上一次迭代中發現的最佳野狗,β2的值與式2.2中的值相同,β2是在[-1,1]區間內均勻生成的隨機數,r1是在從1到最大搜索代理(野狗)大小的區間內生成的隨機數,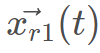 是隨機選擇的第r1個野狗,其中i≠r1。
是隨機選擇的第r1個野狗,其中i≠r1。
在DOA中,野狗的存活率值由下式給出:
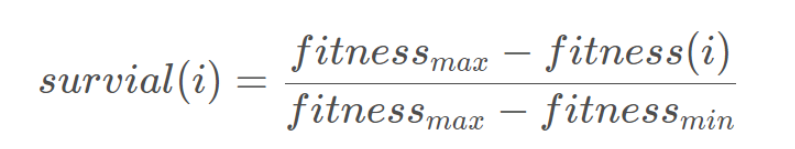
其中,fitnessmax和fitnessmin分別是當前一代中最差和最佳的適應度值,而fitness(i)是第i個野狗的當前適應度值。式(5)中的生存向量包含[0,1]區間內的歸一化適應度。
%====歡迎關注公眾號:電力系統與算法之美====
function DOA()
%% ====參數設置====
popsize=20; % 種群規模
Iteration=1000; % 迭代次數
lb = -10; % 各維度的下限
ub = 10; % 各維度的上限
dim = 2; % 優化變量的個數
P= 0.5; % Hunting or Scavenger rate.
Q= 0.7; % Group attack or persecution?
beta1= -2 + 4* rand(); % -2 < beta < 2
beta2= -1 + 2* rand(); % -1 < beta2 < 1
naIni= 2; % minimum number of dingoes that will attack
naEnd= popsize /naIni; % maximum number of dingoes that will attack
na= round(naIni + (naEnd-naIni) * rand()); % number of dingoes that will attack
%% ====初始化種群位置=====
Positions=lb + (ub - lb).*rand(popsize, dim);
for i=1:size(Positions,1)
Fitness(i)=sum(Positions(i,:).^2); % get fitness
end
[best_score, minIdx]= min(Fitness); % the min fitness value vMin and the position minIdx
best_x= Positions(minIdx,:); % the best vector
[worst_score, ~]= max(Fitness); % the max fitness value vMax and the position maxIdx
curve=zeros(1,Iteration);
%% Section 2.2.4 Dingoes'survival rates
for i=1:size(Fitness,2)
survival(i)= (worst_score-Fitness(i))/(worst_score - best_score);
end
%% =====開始循環===========
for t=1:Iteration
for r=1:popsize
if rand() < P % Hunting
sumatory=0;
c=1;
vAttack=[];
while(c<=na)
idx =round( 1+ (popsize-1) * rand());
band= 0;
for i=1:size(vAttack, 2)
if idx== vAttack(i)
band=1;
break;
end
end
if ~band
vAttack(c) = idx;
c=c+1;
end
end
for j=1:size(vAttack,2)
sumatory= sumatory + Positions(vAttack(j),:)- Positions(r,:);
end
sumatory=sumatory/na;
if rand() < Q % group attack
v(r,:)= beta1 * sumatory-best_x; % Strategy 1: Eq.2
else % Persecution
r1= round(1+ (popsize-1)* rand()); %
v(r,:)= best_x + beta1*(exp(beta2))*((Positions(r1,:)-Positions(r,:))); %
end
else % Scavenger
r1= round(1+ (popsize-1)* rand());
if rand() < 0.5
val= 0;
else
val=1;
end
v(r,:)= (exp(beta2)* Positions(r1,:)-((-1)^val)*Positions(r,:))/2; %
end
if survival(r) <= 0.3 % Section 2.2.4, Algorithm 3 - Survival procedure
band=1;
while band
r1= round(1+ (popsize-1)* rand());
r2= round(1+ (popsize-1)* rand());
if r1 ~= r2
band=0;
end
end
if rand() < 0.5
val= 0;
else
val=1;
end
v(r,:)= best_x + (Positions(r1,:)-((-1)^val)*Positions(r2,:))/2; % Section 2.2.4, Strategy 4: Eq.6
end
% Return back the search agents that go beyond the boundaries of the search space .
Flag4ub=v(r,:)>ub;
Flag4lb=v(r,:)<lb;
v(r,:)=(v(r,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
% Evaluate new solutions
Fnew= sum(v(r,:).^2);
% Update if the solution improves
if Fnew <= Fitness(r)
Positions(r,:)= v(r,:);
Fitness(r)= Fnew;
end
if Fnew <= best_score
best_x= v(r,:);
best_score= Fnew;
end
end
curve(t)= best_score;
[worst_score, ~]= max(Fitness);
for i=1:size(Fitness,2)
survival(i)= (worst_score-Fitness(i))/(worst_score - best_score);
end
end
%======結束優化===============
%% 進化曲線
figure
semilogy(curve,'Color','r','LineWidth',2)
grid on
title('收斂曲線')
xlabel('迭代次數');
ylabel('最佳適應度');
axis tight
legend('DOA')
display(['最優解: ', num2str(best_x)]);
display(['最小值: ', num2str(best_score)]);
end
“基于Matlab怎么實現野狗優化算法”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。