您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了機器學習中如何在統計數據中查找異常值,具有一定借鑒價值,感興趣的朋友可以參考下,希望大家閱讀完這篇文章之后大有收獲,下面讓小編帶著大家一起了解一下。
異常值是數據集的重要組成部分。它們可以保存有關您數據的有用信息。異常值可以為您正在研究的數據提供有用的見解,并且它們可以對統計結果產生影響。這可能會幫助您發現不一致之處并檢測統計過程中的任何錯誤。因此,了解如何在數據集中查找異常值將有助于您更好地理解數據。
有幾種不同的方法可以在統計中找到異常值。本文將解釋如何通過計算四分位距來檢測數值異常值。我舉了一個非常簡單的數據集以及如何計算四分位距的示例,因此您可以根據需要進行操作。讓我們開始吧!
簡單來說,異常值是相對于最近的數據點和您正在使用的數據圖或數據集中的其余相鄰共存值而言極高或極低的數據點。
離群值是從數據集或圖形中的整體值模式中顯著突出的極值。
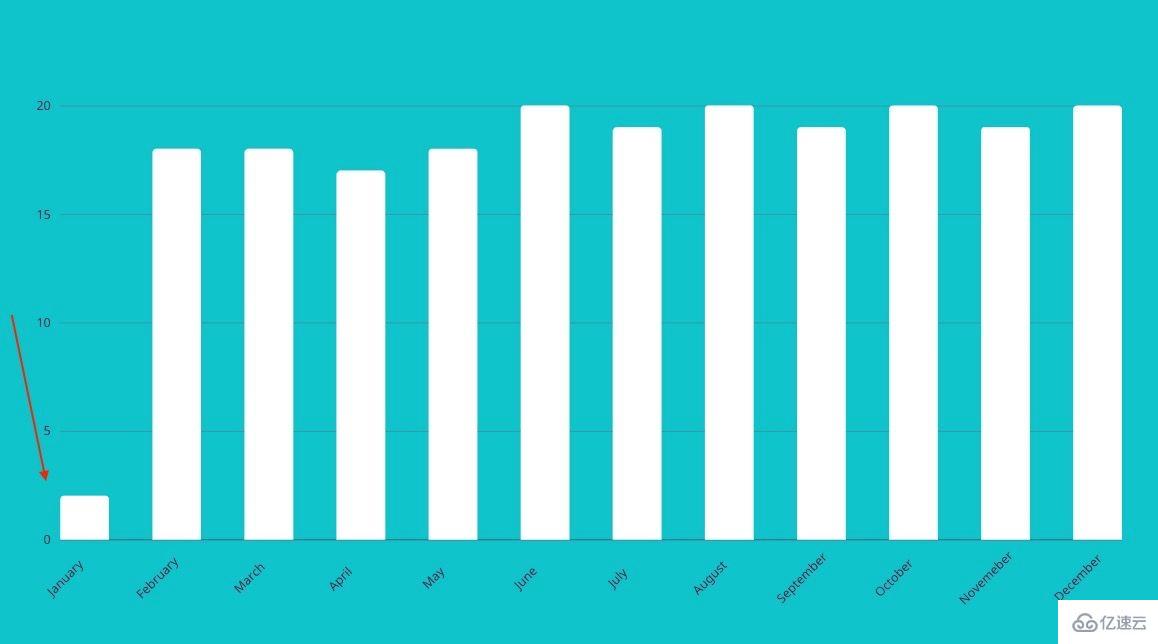
下面,在圖表的最左側,有一個異常值。
一月份的值明顯低于其他月份。
好的,你如何尋找異常值?
異常值必須滿足以下兩個條件之一:
outlier < Q1 - 1.5(IQR)
outlier > Q3 + 1.5(IQR)
低離群值的規則是數據集中的數據點必須小于Q1 - 1.5xIQR。
這意味著數據點需要低于第一個四分位數的四分位間距的 1.5 倍以上才能被視為低異常值。
高離群值的規則是,如果數據集中的任何數據點大于Q3 - 1.5xIQR,則為高離群值。
更具體地說,數據點需要落在第三個四分位數以上的四分位距的 1.5 倍以上才能被視為高異常值。
如您所見,您需要首先在數據集中計算某些個別值,例如IQR. 但是要找到IQR,您需要找到分別是Q1和 的所謂的第一四分位數和第三四分位數 Q3。
所以,讓我們看看它們各自做了什么,并分解如何在奇數和偶數數據集中找到它們的值。
首先,假設您有這個數據集:
25,14,6,5,5,30,11,11,13,4,2
第一步是按數字升序對值進行排序,從最小到最大。
2,4,5,5,6,11,11,13,14,25,30
最低值 ( MIN ) 是2,最高值 ( MAX ) 是30。
下一步是找到中位數或四分位數 2 (Q2)。
這組特定的數據具有奇數個值,11總分加在一起。
在數據集中查找中位數意味著您正在查找中間值——集合中的單個中間數。
在奇數數據集中,只有一個中間數。
因為11總共有值,所以一個簡單的方法是將集合分成兩個相等的部分,每邊包含5值。
中值將5在一側具有值,在另一側具有值5。
(2,4,5,5,6), 11,(11,13,14,25,30)
中位數是11因為它是將前半部分與后半部分分開的數字。
仔細檢查您是否正確的另一種方法是這樣做:
(total_number_of_scores + 1) / 2.
這是(11 + 1) /2 = 6,這意味著您希望在6th這組數據的位置使用數字 - 即11。
所以Q2 = 11。
接下來,為了找到下四分位數,Q1我們需要找到數據集前半部分的中位數,它位于左側。
提醒一下,初始數據集是:
(2,4,5,5,6), 11,(11,13,14,25,30)
數據集的前半部分或下半部分不包括中位數:
2,4,5,5,6
這一次,又是一組奇怪的分數——特別是有5值。
您想再次將這半集分成另一半,每側有相同數量的兩個值。您將獲得一個唯一編號,該編號將是5值中間的編號。
選擇突出的中間值:
(2,4), 5,(5,6)
在這種情況下,它是Q1 = 5.
要仔細檢查,您還可以執行total_number_of_values + 1 / 2類似于前面的示例:
(5 + 1) /2 = 3.
這意味著您需要第三位的數字,即5.
要找到上四分位數Q3,過程與Q1上述相同。但在這種情況下,你在數據集的右側取下半部分,高于中位數,不包括中位數本身:
(2,4,5,5,6), 11,(11,13,14,25,30)
11,13,14,25,30
您將奇數集的這一半拆分為另一半以求中位數,然后求出 的值Q3。
您再次希望像上半場一樣排在第三位。
(11,13), 14,(25,30)
所以Q3 = 14。
現在,下一步是計算代表四分位距的 IQR。
這是您在上面計算的下四分位數 (Q1) 和上四分位數 (Q3) 之間的差異/距離。
提醒一下,這樣做的公式如下:
IQR = Q3 - Q1
要從上面找到數據集的 IQR:
IQR= 14 - 5 IQR = 9
回顧到目前為止,數據集如下:
2,4,5,5,6,11,11,13,14,25,30
到目前為止,您已經計算了五個數字摘要:
MIN = 2 Q1 = 5 MED = 11 Q3 = 14 MAX = 30
最后,讓我們看看數據集中是否有任何異常值。
提醒一下,異常值必須符合以下標準:
outlier < Q1 - 1.5(IQR)
或者
outlier > Q3 + 1.5(IQR)
要查看是否有最低值異常值,需要計算第一部分,看看集合中是否有滿足條件的數字。
Outlier < Q1 - 1.5(IQR) Outlier < 5 - 1.5(9) Outlier < 5 - 13.5 outlier < - 8.5
沒有更低的異常值,因為沒有比-8.5數據集中的數字少的數字。
接下來,查看是否有更高的異常值:
Outlier > Q3 + 1.5(IQR)= Outlier > 14 + 1.5(9) Outlier > 14 + 13.5 Outlier > 27,5
并且數據集中有一個數字大于27,5:
2,4,5,5,6,11,11,13,14,25,30
在這種情況下,30是現有數據集中的異常值。
當您的數據集由一組偶數數據組成時會發生什么?
不僅有一個突出的中位數 (Q2),也沒有突出的上四分位數 (Q1) 或突出的下四分位數 (Q3)。
所以計算四分位數然后找到異常值的過程有點不同。
假設你有這個帶有8數字的數據集:
10,15,20,26,28,30,35,40
這一次,數字已經從最低值到最高值排序。
要在偶數數據集中找到中位數,您需要找到位于中間的兩個數字之間的值。您將它們加在一起并除以2,如下所示:
10,15,20, 26,28,30,35,40
26 + 28 = 54 54 / 2 = 27
要計算偶數數據集中的上四分位數和下四分位數,您需要保留數據集中的所有數字(而不是在您刪除中位數的奇數集中)。
這一次,數據集被切成兩半。
10,15,20,26 | 28,30,35,40
為了 find Q1,您將數據集的前半部分拆分為另一半,留下剩余的偶數集:
10,15 | 20,26
要找到這一半的中位數,您可以將中間的兩個數字除以二:
Q1 = (15 + 20)/2 Q1 = 35 / 2 Q1 = 17,5
要找到Q3,您需要關注數據集的后半部分并將該半部分拆分為另一半:
28,30,35,40 -> 28,30 | 35,40
中間的兩個數字是30和35。
您將它們相加并將它們除以二,結果是:
Q3 = (30 + 35)/2 Q3 = 65 / 2 Q3 = 32,5
計算 IQR 的公式與我們用于計算奇數數據集的公式完全相同。
IQR = Q3 - Q1 IQR = 32,5 - 17,5 IQR = 15
回顧一下,到目前為止,五個數字摘要如下:
MIN = 10 Q1 = 17,5 MED = 27 Q3 = 32,5 MAX = 40
要計算數據集中的任何異常值:
outlier < Q1 - 1.5(IQR)
或者
outlier > Q3 + 1.5(IQR)
要找到任何較低的異常值,您可以計算Q1 - 1.5(IQR)并查看是否有任何值小于結果。
outlier < 17,5 - 1.5(15)= outlier < 17,5 - 22,5 outlier < -5
數據集中沒有任何小于 的值-5。
最后,為了找到任何更高的異常值,您計算 Q3 - 1.5(IQR)并查看數據集中是否有任何值高于結果
outlier > 32.5 + 1.5(15)= outlier > 32.5 + 22.5 outlier > 55
沒有任何高于55此數據集的值,因此該數據集沒有任何異常值。
感謝你能夠認真閱讀完這篇文章,希望小編分享的“機器學習中如何在統計數據中查找異常值”這篇文章對大家有幫助,同時也希望大家多多支持億速云,關注億速云行業資訊頻道,更多相關知識等著你來學習!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。