您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“python實現層次聚類的方法是什么”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
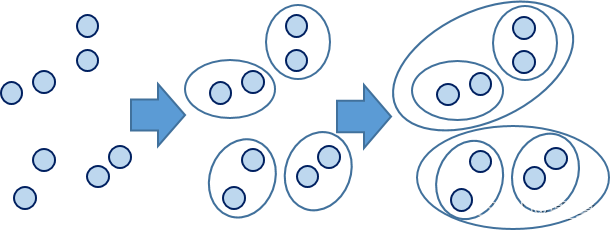
顧名思義,層次聚類就是一層一層的進行聚類,可以由上向下把大的類別(cluster)分割,叫作分裂法;也可以由下向上對小的類別進行聚合,叫作凝聚法;但是一般用的比較多的是由下向上的凝聚方法。
分裂法指的是初始時將所有的樣本歸為一個類簇,然后依據某種準則進行逐漸的分裂,直到達到某種條件或者達到設定的分類數目。用算法描述:
輸入:樣本集合D,聚類數目或者某個條件(一般是樣本距離的閾值,這樣就可不設置聚類數目)
輸出:聚類結果
1.將樣本集中的所有的樣本歸為一個類簇;
repeat:
2.在同一個類簇(計為c)中計算兩兩樣本之間的距離,找出距離最遠的兩個樣本a,b;
3.將樣本a,b分配到不同的類簇c1和c2中;
4.計算原類簇(c)中剩余的其他樣本點和a,b的距離,若是dis(a)<dis(b),則將樣本點歸到c1中,否則歸到c2中;
util: 達到聚類的數目或者達到設定的條件
凝聚法指的是初始時將每個樣本點當做一個類簇,所以原始類簇的大小等于樣本點的個數,然后依據某種準則合并這些初始的類簇,直到達到某種條件或者達到設定的分類數目。用算法描述:
輸入:樣本集合D,聚類數目或者某個條件(一般是樣本距離的閾值,這樣就可不設置聚類數目)
輸出:聚類結果
1.將樣本集中的所有的樣本點都當做一個獨立的類簇;
repeat:
2.計算兩兩類簇之間的距離(后邊會做介紹),找到距離最小的兩個類簇c1和c2;
3.合并類簇c1和c2為一個類簇;
util: 達到聚類的數目或者達到設定的條件
例圖:
歐式距離的計算公式
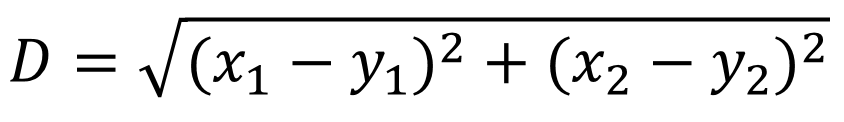
類簇間距離的計算方法有許多種:
(1)就是取兩個類中距離最近的兩個樣本的距離作為這兩個集合的距離,也就是說,最近兩個樣本之間的距離越小,這兩個類之間的相似度就越大
(2)取兩個集合中距離最遠的兩個點的距離作為兩個集合的距離
(3)把兩個集合中的點兩兩的距離全部放在一起求一個平均值,相對也能得到合適一點的結果。
e.g.下面是計算組合數據點(A,F)到(B,C)的距離,這里分別計算了(A,F)和(B,C)兩兩間距離的均值。
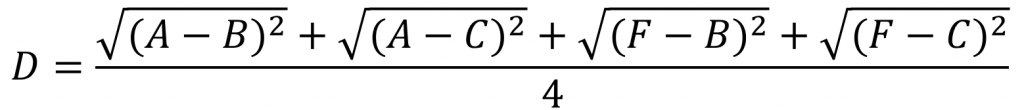
(4)取兩兩距離的中值,與取均值相比更加能夠解除個別偏離樣本對結果的干擾。
(5)求每個集合的中心點(就是將集合中的所有元素的對應維度相加然后再除以元素個數得到的一個向量),然后用中心點代替集合再去就集合間的距離
接下來以世界銀行樣本數據集進行簡單實現。該數據集以標準格式存儲在名為WBClust2013.csv的CSV格式的文件中。其有80行數據和14個變量。數據來源
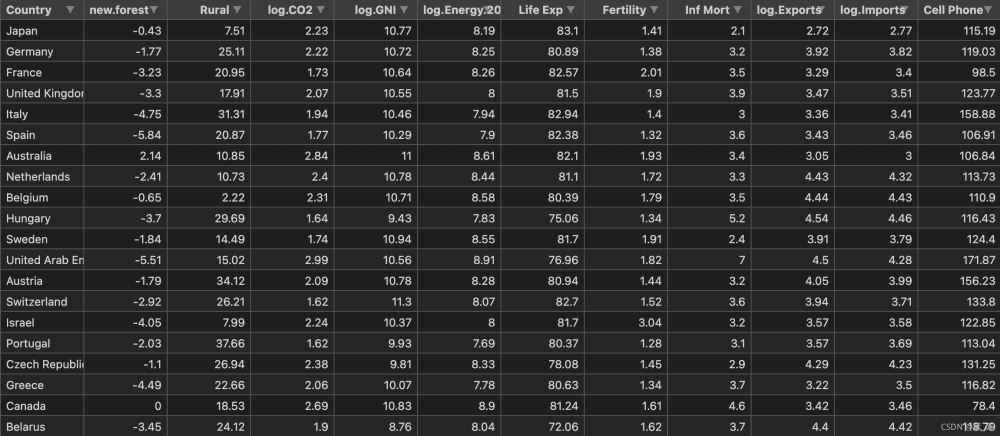
為了使得結果可視化更加方便,我將最后一欄人口數據刪除了。并且在實現層次聚類之后加入PCA降維與原始結果進行對比。
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster
import matplotlib.pyplot as plt
import pandas as pd
import numpy as np
data = pd.read_csv('data/WBClust2013.csv')
data.pop('Pop')
# data.pop('RuralWater')
# data.pop('CellPhone')
# data.pop('LifeExp')
data = data[:20]
country = list(data['Country'])
data.pop('Country')
# 以下代碼為僅使用層次聚類
plt.figure(figsize=(9, 7))
plt.title("original data")
mergings = linkage(data, method='average')
# print(mergings)
dendrogram(mergings, labels=country, leaf_rotation=45, leaf_font_size=8)
plt.show()
Z = linkage(data, method='average')
print(Z)
cluster_assignments = fcluster(Z, t=3.0, criterion='maxclust')
print(cluster_assignments)
for i in range(1, 4):
print('cluster', i, ':')
num = 1
for index, value in enumerate(cluster_assignments):
if value == i:
if num % 5 == 0:
print()
num += 1
print(country[index], end=' ')
print()
# 以下代碼為加入PCA進行對比
class myPCA():
def __init__(self, X, d=2):
self.X = X
self.d = d
def mean_center(self, data):
"""
去中心化
:param data: data sets
:return:
"""
n, m = data.shape
for i in range(m):
aver = np.sum(self.X[:, i])/n
x = np.tile(aver, (1, n))
self.X[:, i] = self.X[:, i]-x
def runPCA(self):
# 計算協方差矩陣,得到特征值,特征向量
S = np.dot(self.X.T, self.X)
S_val, S_victors = np.linalg.eig(S)
index = np.argsort(-S_val)[0:self.d]
Y = S_victors[:, index]
# 得到輸出樣本集
Y = np.dot(self.X, Y)
return Y
# data_for_pca = np.array(data)
# pcaObject=myPCA(data_for_pca,d=2)
# pcaObject.mean_center(data_for_pca)
# res=pcaObject.runPCA()
# plt.figure(figsize=(9, 7))
# plt.title("after pca")
# mergings = linkage(res,method='average')
# print(mergings)
# dendrogram(mergings,labels=country,leaf_rotation=45,leaf_font_size=8)
# plt.show()
# Z = linkage(res, method='average')
# print(Z)
# cluster_assignments = fcluster(Z, t=3.0, criterion='maxclust')
# print(cluster_assignments)
# for i in range(1,4):
# print('cluster', i, ':')
# num = 1
# for index, value in enumerate(cluster_assignments):
# if value == i:
# if num % 5 ==0:
# print()
# num+=1
# print(country[index],end=' ')
# print()兩次分類結果都是一樣的:
cluster 1 : China United States Indonesia Brazil Russian Federation Japan Mexico Philippines Vietnam Egypt, Arab Rep. Germany Turkey Thailand France United Kingdom cluster 2 : India Pakistan Nigeria Bangladesh cluster 3 : Ethiopia
通過樹狀圖對結果進行可視化
“python實現層次聚類的方法是什么”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。