編程中遞歸與排序分別是什么

這篇文章主要介紹“編程中遞歸與排序分別是什么”，在日常操作中，相信很多人在編程中遞歸與排序分別是什么問題上存在疑惑，小編查閱了各式資料，整理出簡單好用的操作方法，希望對大家解答”編程中遞歸與排序分別是什么”的疑惑有所幫助！接下來，請跟著小編一起來學習吧！

遞歸

遞歸需要滿足的三個條件

• 一個問題的解可以分為幾個子問題的解

• 此問題與子問題，除了數據規模不一樣，求解思路完全一樣

• 存在遞歸終止條件

怎么寫遞歸代碼

寫遞歸代碼的關鍵就是找到如何將大問題分解為小問題的規律，并且基于此寫出遞推公式，然后再推敲終止條件，最后將遞推公式和終止條件翻譯成代碼。
只要遇到遞歸，我們就把它抽象成一個遞推公式，不用想一層層的調用關系，不要試圖用人腦去分解遞歸的每個步驟。

遞歸注意事項

警惕堆棧溢出

如果遞歸調用層很深，則有可能會出現堆棧溢出；可通過限制最大深度解決此問題：超過一定的深度直接返回報錯。

避免重復計算

通過散列表保存已求解過的表達式；當遞歸調用到此表達式時，先判斷是夠已求解過。

排序

最常見的排序：冒泡排序、插入排序、選擇排序、歸并排序、快速排序、計數排序、基數排序、桶排序。

如何分析一個算法

排序算法的執行效率

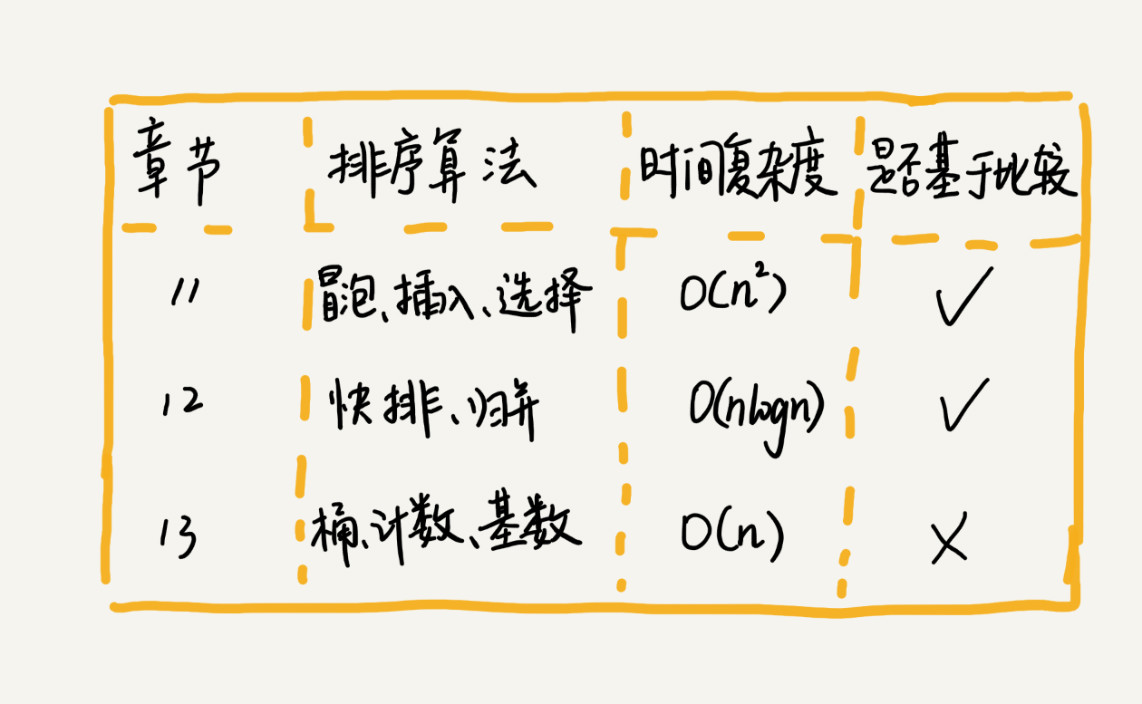
• 最好、最壞、平均情況時間復雜度

• 時間復雜度的系數、常數、低階

• 比較次數和交換(或移動)次數

排序算法的內存消耗

算法的內存消耗可以通過空間復雜度來衡量；原地排序特指空間復雜度為O(1)的排序算法

排序算法的穩定性

待排序的序列中存在值相等的元素，經過排序之后，相等元素之間原有的先后順序不變。
穩定的排序算法可以保持相同的兩個對象，在排序之后的前后順序不變。

冒泡排序

冒泡排序只操作相鄰的兩個元素，每次操作時比較相鄰的兩個元素判斷是否滿足大小關系要求，不滿足時就交換位置。

• 從執行效率上看：冒泡排序的最好情況時間復雜度為O(n),最壞情況時間復雜度為O(n^2 ),平均情況時間復雜度為O(n^2 )。

• 從內存消耗上看：冒泡排序只涉及相鄰元素交換操作，所以空間復雜度為O(1),是一個原地排序算法。

• 從穩定性上看：相鄰兩個元素大小相等時我們不做交換，所以大小相等的兩個元素在排序后順序不會改變，屬于穩定的排序算法。

代碼實現

public static <T extends Comparable> T[] bubbleSort(T[] arrays) {
    for (int i = 0; i < arrays.length; i++) {
        boolean unUse = true;
        for (int j = 1; j < arrays.length - i; j++) {
            //如果前一個元素大于當前元素 就交換雙方位置
            if (arrays[j - 1].compareTo(arrays[j]) > 0) {
                T t = arrays[j - 1];
                arrays[j - 1] = arrays[j];
                arrays[j] = t;
                unUse = false;
            }
        }
        //如果整輪下來沒有交換動作，說明排序已完成
        if (unUse) break;
    }
    return arrays;
}

插入排序

插入排序將數組分為已排序區和未排序區，核心思想是取未排序區的元素在已排序區中找到合適的位置插入，保證已排序區的數據一直是有序的。

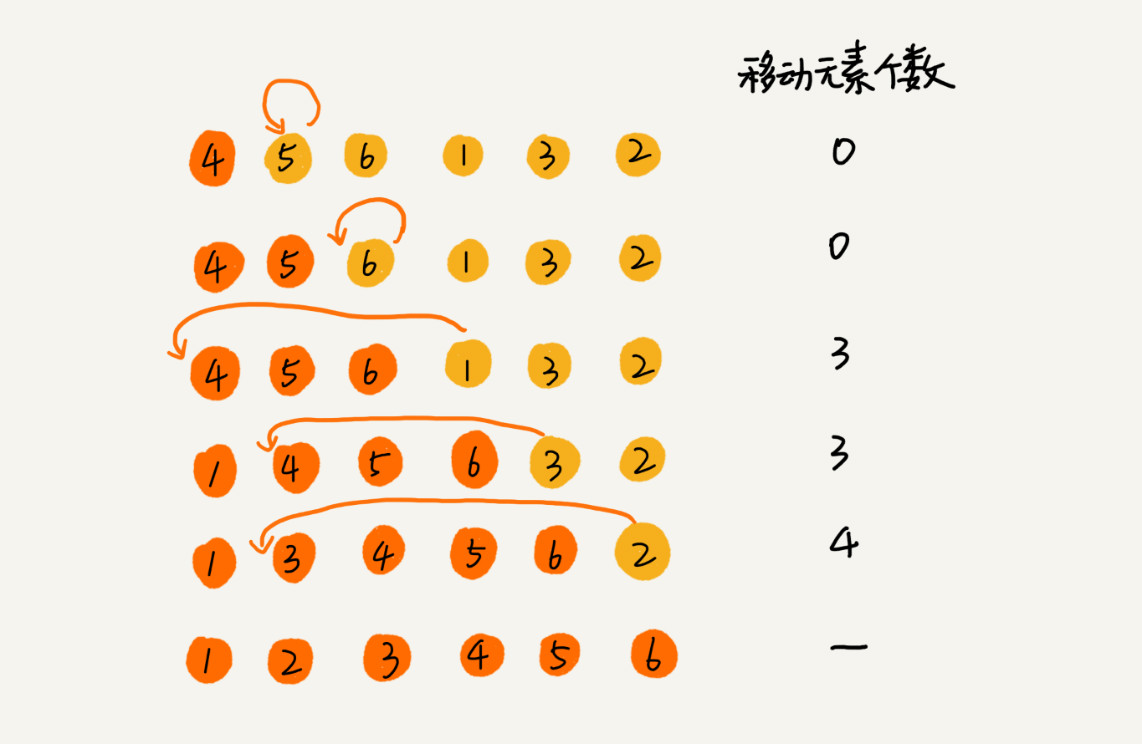
• 從執行效率上看，插入排序的最好情況時間復雜度為O(n),最壞情況時間復雜度為O(n^2 ),平均情況時間復雜度為O(n^2 )。

• 從內存消耗上看：插入排序也不需要額外的存儲空間，所以空間復雜度為O(1),是一個原地排序算法。

• 從穩定性上看：對于值相同的元素，后面出現的元素插入到前面出現元素的后面，所以兩個元素在排序后順序不會改變，屬于穩定的排序算法。

代碼實現

public static <T extends Comparable> T[] insertionSort(T[] arrays) {
    if (arrays.length < 2) return arrays;
    for (int i = 1; i < arrays.length; i++) {
        T t = arrays[i];
        for (int j = 0; j < i; j++) {
            if (t.compareTo(arrays[j]) < 0) {
                System.arraycopy(arrays, j, arrays, j + 1, i - j);
                arrays[j] = t;
                break;
            }
        }
    }
    return arrays;
}

選擇排序

選擇排序也是將數據分為已排序區和未排序區，和插入排序不同的是：每次將未排序區中最小的元素放入到已排序區的尾部。

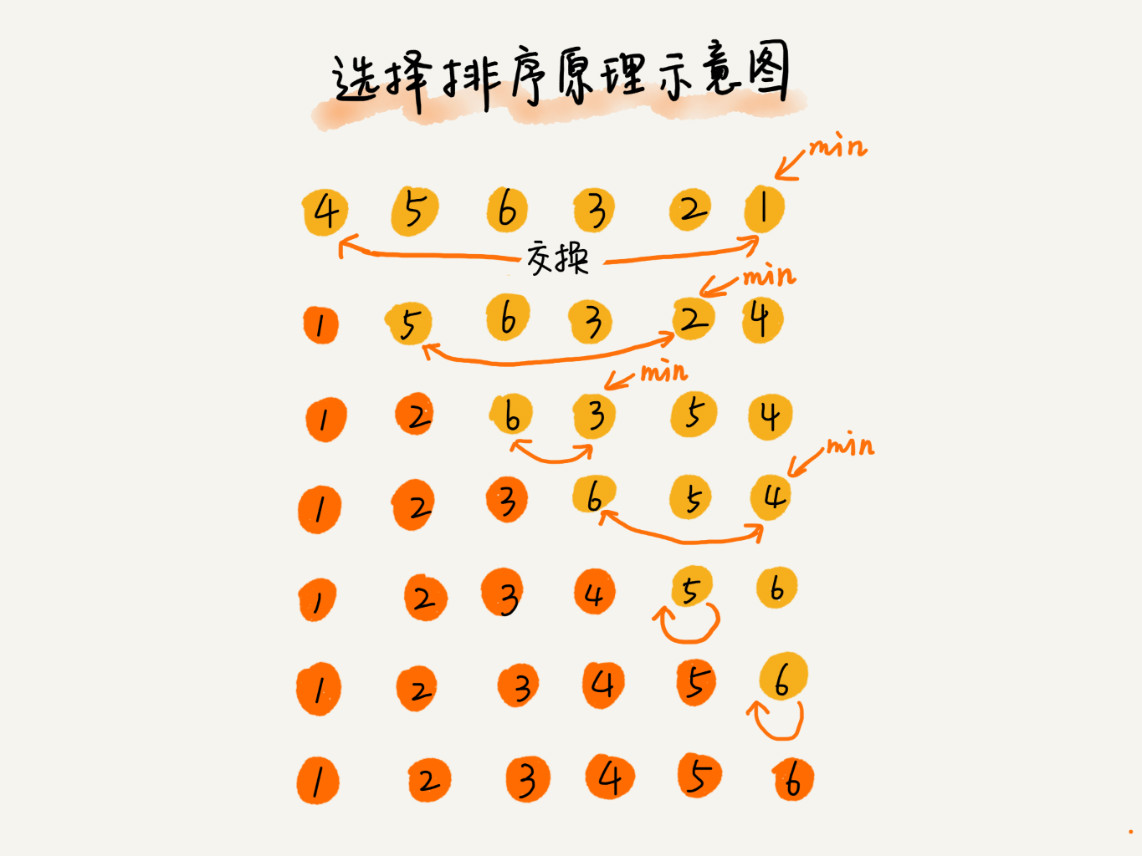
• 從執行效率上看，插入排序的最好情況時間復雜度為O(n^2 ),最壞情況時間復雜度為O(n^2 ),平均情況時間復雜度也為O(n^2 )。

• 從內存消耗上看：選擇排序也不需要額外的存儲空間，所以空間復雜度為O(1),是一個原地排序算法。

• 從穩定性上看：未排序區最小元素與首元素交換位置時，可能會改變相同值的兩個元素的順序，所以選擇排序屬于不穩定的排序算法。

代碼實現

public static <T extends Comparable> T[] selectionSort(T[] arrays) {
    if (arrays.length < 2) return arrays;
    for (int i = 0; i < arrays.length; i++) {
        int minIndex = i;//定義最小值索引
        T min = arrays[minIndex];//默認第一個是最小值
        for (int j = i + 1; j < arrays.length; j++) {
            if (arrays[j].compareTo(min) < 0) {
                minIndex = j;
                min = arrays[minIndex];
            }
        }
        //交換值
        arrays[minIndex] = arrays[i];
        arrays[i] = min;
    }
    return arrays;
}

總結

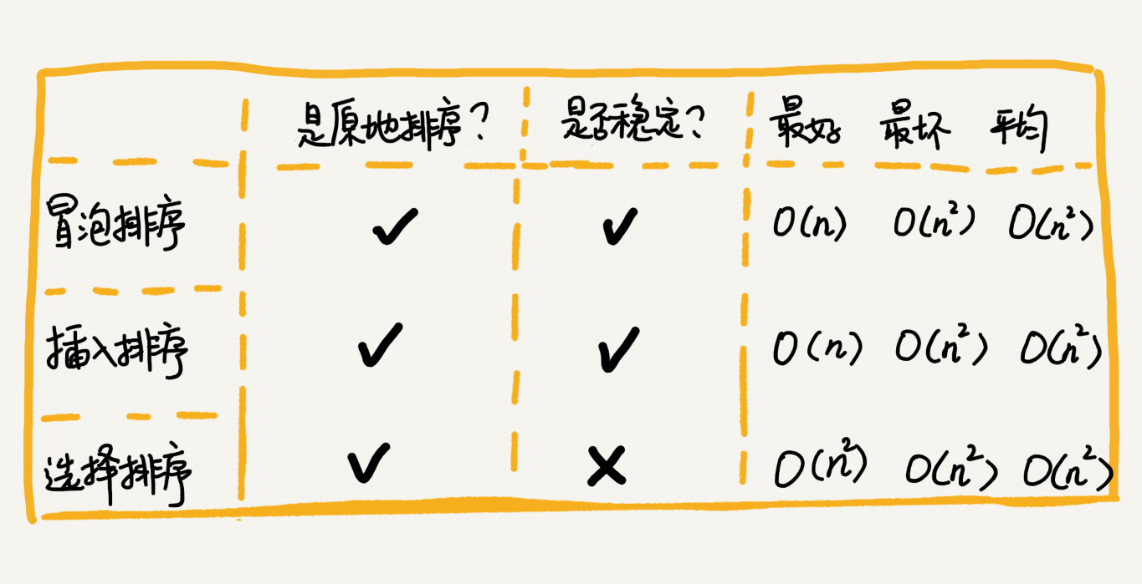
我們從執行效率、內存消耗和穩定性三個方面分析了三種時間復雜度為O(n^2 )的排序算法：

到此，關于“編程中遞歸與排序分別是什么”的學習就結束了，希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習，快去試試吧！若想繼續學習更多相關知識，請繼續關注億速云網站，小編會繼續努力為大家帶來更多實用的文章！