Python如何實現線性規劃

本文小編為大家詳細介紹“Python如何實現線性規劃”，內容詳細，步驟清晰，細節處理妥當，希望這篇“Python如何實現線性規劃”文章能幫助大家解決疑惑，下面跟著小編的思路慢慢深入，一起來學習新知識吧。

 運籌學

運籌學是一種科學的決策方法，它通常是在需要分配稀缺資源的條件下，尋求系統的優秀設計。科學的決策方法需要使用一個或多個數學模型(優化模型)來做出最優決策。

優化模型試圖在滿足給定約束的決策變量的所有值的集合中，找到優化(最大化或最小化)目標函數的決策變量的值。 它的三個主要組成部分是：

1. 目標函數:要優化的函數(最大化或最小化)。

2. 決策變量:影響系統性能的可控變量。

3. 約束:決策變量的一組約束(即線性不等式或等式)。非負性約束限制了決策變量取正值。

優化模型的解稱為最優可行解。

建模步驟

對運籌學問題進行準確建模是很重要的任務，也是很困難的任務。錯誤的模型會導致錯誤的解決方案，從而不能解決原來的問題。團隊成員應按照以下步驟進行建模：

1. 問題定義:定義項目的范圍，并確定三個要素:決策變量、目標和限制(即約束)。

2. 模型構建:將問題定義轉化為數學關系。

3. 模型求解:使用標準優化算法。在獲得解后，需要進行靈敏度分析，以找出由于某些參數的變化而導致的解的行為。

4. 模型有效性:檢查模型是否按預期工作。

5. 實現:將模型和結果轉換為解決方案。

線性規劃

線性規劃(Linear  Programming，也稱為LP)是一種運籌學技術，當當所有的目標和約束都是線性的(在變量中)并且當所有的決策變量都是連續的時使用。線性規劃是最簡單的運籌學方法。

Python的SciPy庫包含用于解決線性編程問題的linprog函數。在使用linprog時，編寫代碼要考慮的兩個注意事項：

1. 這個問題必須表述為一個最小化問題。

2. 不等式必須表示為≤。

最小化問題

讓我們考慮以下要解決的最小化問題：

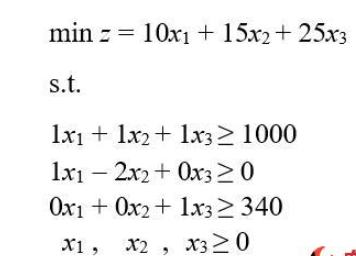
讓我們看一下Python代碼：

# Import required libraries import numpy as np from scipy.optimize import linprog  # Set the inequality constraints matrix # Note: the inequality constraints must be in the form of <= A = np.array([[-1, -1, -1], [-1, 2, 0], [0, 0, -1], [-1, 0, 0], [0, -1, 0], [0, 0, -1]])  # Set the inequality constraints vector b = np.array([-1000, 0, -340, 0, 0, 0])  # Set the coefficients of the linear objective function vector c = np.array([10, 15, 25])  # Solve linear programming problem res = linprog(c, A_ub=A, b_ub=b)  # Print results print('Optimal value:', round(res.fun, ndigits=2),       '\nx values:', res.x,       '\nNumber of iterations performed:', res.nit,       '\nStatus:', res.message)

輸出結果：

# Optimal value: 15100.0  # x values: [6.59999996e+02 1.00009440e-07 3.40000000e+02]  # Number of iterations performed: 7  # Status: Optimization terminated successfully.

最大化問題

由于Python的SciPy庫中的linprog函數是用來解決最小化問題的，因此有必要對原始目標函數進行轉換。通過將目標函數的系數乘以-1(即通過改變其符號)，可以將最小化問題轉化為一個最大化問題。

讓我們考慮下面需要解決的最大化問題:

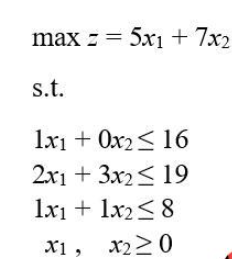
讓我們看一下Python的實現：

# Import required libraries import numpy as np from scipy.optimize import linprog  # Set the inequality constraints matrix # Note: the inequality constraints must be in the form of <= A = np.array([[1, 0], [2, 3], [1, 1], [-1, 0], [0, -1]])  # Set the inequality constraints vector b = np.array([16, 19, 8, 0, 0])  # Set the coefficients of the linear objective function vector # Note: when maximizing, change the signs of the c vector coefficient c = np.array([-5, -7])  # Solve linear programming problem res = linprog(c, A_ub=A, b_ub=b)  # Print results print('Optimal value:', round(res.fun*-1, ndigits=2),       '\nx values:', res.x,       '\nNumber of iterations performed:', res.nit,       '\nStatus:', res.message)

上述代碼的輸出結果為：

# Optimal value: 46.0  # x values: [5. 3.]  # Number of iterations performed: 5  # Status: Optimization terminated successfully.

讀到這里，這篇“Python如何實現線性規劃”文章已經介紹完畢，想要掌握這篇文章的知識點還需要大家自己動手實踐使用過才能領會，如果想了解更多相關內容的文章，歡迎關注億速云行業資訊頻道。