您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“Spark GraphX怎么使用”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
在Spark年幼的時候,0.5版本就已經帶了一個Bagel小模塊,提供了類似Pregel的功能,當然,這個版本還非常的原始,性能和功能都比較弱,屬于實驗型產品。到0.8版本的時候,鑒于業界對分布式圖計算的需求日益見漲,Spark開始獨立一個分支:Graphx-Branch,做為獨立的圖計算模塊,借鑒GraphLab,開始設計開發GraphX。在0.9版本中,這個模塊被正式集成到主干,雖然是alpha版本,但是已經可以開始進行試用,小面包圈Bagel告別舞臺。1.0版本,GraphX正式投入生產使用。
值得留意的是,GraphX目前依然處于快速發展中,從0.8的分支,到0.9和1.0,每個版本代碼都有不少的改進和重構,并根據觀察,在沒有改任何代碼邏輯和運行環境,只是升級版本,切換接口和重新編譯的情況下,每個版本能夠有10-20%的性能提升。雖然和GraphLab的性能還有一定的差距,但是憑借著Spark整體的一體化流水線處理,社區熱烈的活躍度以及快速改進速度,使得它具有強大的競爭力。
在正式介紹GraphX之前,先看看通用的分布式圖計算框架。簡單來說,分布式圖計算框架的目的,就是將對于巨型圖的各種操作,包裝為簡單的接口,讓分布式存儲,并行計算等復雜問題對上層透明。從而使得復雜網絡和圖算法的工程師,可以更加聚焦在圖相關的模型設計和使用上,而不用關心底層的分布式細節。為了實現該目的,需要解決兩個通用的問題。
巨型圖的存儲總體上有邊分割和點分割兩種存儲方式。2013年GraphLab2.0推出,將其存儲方式由邊分割變為點分割,在性能上取得重大提升,目前基本上被業界廣泛接受并使用。
邊分割(Edge Cut)
每個頂點都存儲一次,但是有的邊會被打斷,被分到了兩臺機器上。這樣做的好處是節省存儲空間,壞處是對于圖進行基于邊的計算時,對于一條兩個頂點被分到不同機器上的邊來說,要跨機器通信傳輸數據,內網通信流量大。
點分割(Vertex Cut)
每個邊都只存儲一次,都只會出現在一臺機器上。鄰居多的點會被復制到多臺機器上,增加存儲開銷,同時會引發數據同步的問題。好處是可以大幅減少內網通信量可以大大降低。
原本兩種方法互有利弊,但現在是點分割占上風,各種分布式圖計算框架,都把自己底層的存儲形式變成了點分割。主要原因有2個:
磁盤的價格下降,存儲空間不是問題了,但是內網的通信資源沒有突破性進展,集群計算時內網帶寬是寶貴的,時間比磁盤更珍貴,這點就類似于常見的空間換時間的策略。
在當前的應用場景中,絕大多數網絡都是“無尺度網絡”,遵循冪律分布,不同點的鄰居數量非常懸殊,邊分割會使得那些多鄰居的點所相連的邊大多數都會被分到不同的機器上,這樣的數據分布會使得內網帶寬更加捉襟見肘,于是邊分割的存儲方式就被漸漸拋棄了
目前的圖計算框架,基本上都是遵循BSP計算模式。BSP全稱Bulk Synchronous Parallell,由哈佛大學Leslie Valiant和牛津大學Bill McColl提出。在BSP中,一次計算過程由一系列全局超步組成,每一個超步由并發計算,通訊, 柵欄同步三個步驟組成。同步完成,標志著該一個超步的完成,以及下一個超步的開始。
BSP模式很簡潔,基于BSP模式,目前有2種比較成熟的圖計算模型:
Pregel模型——“像頂點一樣思考”
2010年,Google的新的三架馬車Caffeine、Pregel、Dremel發布。伴隨著Pregel,BSP模型被廣為人知。據說Pregel的名字是為了紀念歐拉的七橋問題,那七座橋所在的河流,就是叫Pregel。
Pregel借鑒MapReduce的思想,提出了"像頂點一樣思考(Think Like A Vertex)"的圖計算模式,讓用戶無需考慮并行分布式計算的細節,只需要實現一個頂點更新函數,讓框架在遍歷頂點時進行調用即可。
常見的代碼模板如下所示:
void Compute(MessageIterator* msgs) {
//遍歷由頂點入邊傳入的消息列表
for (; !msgs->Done(); msgs->Next())
doSomething()
//生成新的頂點值
*MutableVertexValue() = ...
//生成沿頂點出邊發送的消息
SendMessageToAllNeighbors(...);
}
這個模型雖然簡潔,但是很容易發現它的缺陷。對于鄰居數很多的頂點,它需要處理的消息非常龐大,而在這個模式下,它們是無法被并發處理的。所以對于符合冪律分布的自然圖,這種計算模型下,很容易發生假死或者崩潰。
GAS模型——鄰居更新模型
相比于Pregel模型的消息通信范式,GraphLab的GAS模型更偏向共享內存風格。它允許用戶的自定義函數訪問當前頂點的整個鄰域,可以抽象成Gather,Apply,Scatter這三個階段,常被簡稱為GAS。相應用戶需要實現的三個獨立的函數:gather、apply和scatter。
常見的代碼模板如下所示:
//從鄰居點和邊收集數據
Message gather(Vertex u, Edge uv, Vertex v) {
Message msg = ...
return msg
}
//匯總函數
Message sum(Message left, Message right) {
return left+right
}
//更新頂點Master
void apply(Vertex u, Message sum) {
u.value = ...
}
//更新鄰邊和鄰居點
void scatter(Vertex u, Edge uv, Vertex v) {
uv.value = ...
if ((|u.delta|>ε) Active(v)
}
由于gather/scatter函數是以單條邊為操作粒度,那么對于一個頂點的眾多鄰邊,可以分別由相應的worker獨立地調用gather/scatter函數。這一設計主要是為了適應點分割的圖存儲模式,從而避免Pregel模型會遇到的問題。
在GraphX設計的時候,點分割和GAS都已經成熟了,所以GraphX一開始就站在了巨人的肩膀上,并在設計和編碼中,針對這些問題進行了優化,在功能和性能之間尋找最佳的平衡點。
每個Spark子模塊,如同Spark本身一樣,都有一個核心的抽象。GraphX的核心抽象是Resilient Distributed Property Graph,一種點和邊都帶屬性的有向多重圖。它擴展了Spark RDD的抽象,擁有Table和Graph兩種視圖,而只需要一份物理存儲。而兩種視圖都有自己的獨有的操作符,從而獲得靈活操作和執行效率。
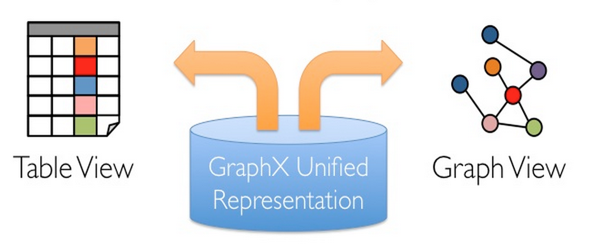
如同Spark一樣,GraphX的代碼依然非常簡潔。核心的GraphX代碼只有3千多行,而在此之上實現的Pregel模型,只要短短的二十多行。GraphX的代碼結構整體如下:
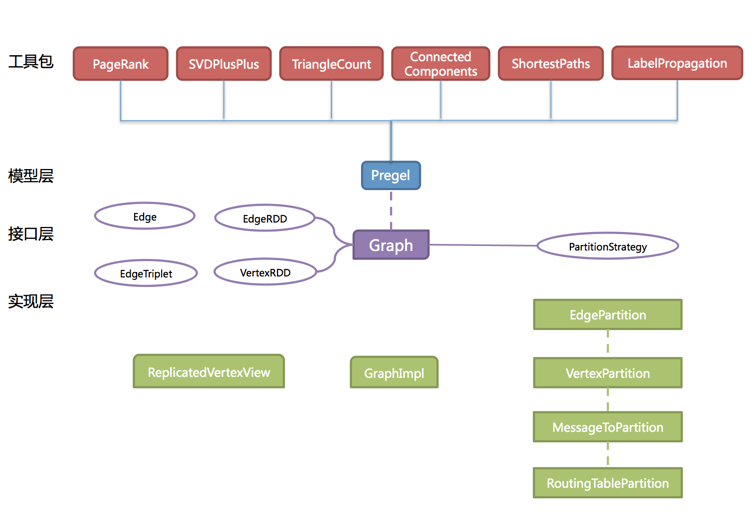
整體還是很清晰明了,其中大部分的impl包的實現,都是圍繞著Partition而優化和進行。這種某種程度上說明了,點分割的存儲和相應的計算優化,的確是圖計算框架的重點和難點。
GraphX的底層設計有幾個關鍵點
對Graph視圖的所有操作,最終都會被轉換成其關聯的Table視圖的RDD操作來完成。這樣對一個圖的計算,最終在邏輯上,等價于一系列RDD的轉換過程。因此,其實Graph最終是具備了的RDD的3個關鍵特性:Immutable,Distributed,Fault-Tolerant。其中最關鍵的是不可變(Immutable)性,所有圖的轉換和操作,邏輯上都是產生了一個新圖,物理上,Graphx會有一定程度的不變頂點和邊的復用優化,對用戶透明。
兩種視圖底層共用的物理數據,由RDD[VertexPartition]和RDD[EdgePartition]這兩個RDD組成。點和邊實際都不是以表Collection[tuple]的形式存儲的,而是由VertexPartition/EdgePartition,在內部存儲一個帶索引結構的分片數據塊,以加速不同視圖下的遍歷速度。不變的索引結構在RDD轉換過程中是共用的,降低了計算和存儲開銷。
圖的分布式存儲采用點分割模式,而且使用partitionBy方法,由用戶指定不同的劃分策略(PartitionStrategy)。劃分策略會將邊分配到各個EdgePartition,頂點Master分配到各個VertexPartition,EdgePartition也會緩存本地邊的關聯點的Ghost副本。劃分策略的不同會影響到所需要緩存的Ghost副本數量,以及每個EdgePartition分配的邊的均衡程度,需要根據圖的結構特征進行選取最佳的Strategy。目前有EdgePartition2d,EdgePartition1d,RandomVertexCut,CanonicalRandomVertexCut這4種策略。目前試驗的結果,在淘寶大部分場景下,EdgePartition2d效果最好。
如同Spark一樣,GraphX的Graph類,提供了豐富的圖運算符,大致結構如下:
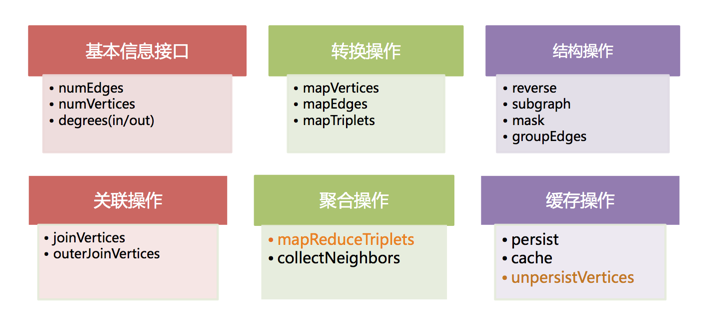
具體每個方法的說明和用法,可以在官方的GraphX Programming Guide找到每個函數的詳細說明,就不一一列舉。重點講幾個需要注意的方法:
由于一個圖,是由3個RDD組成的,所以會占用更多的內存。相應圖的cache,unpersist和checkpoint,更需要留意使用技巧。出于最大限度的復用邊的理念,GraphX的默認接口,只提供了unpersistVertices的方法,如果要釋放邊,需要自己調用g.edges.unpersist()方法才能釋放,這個給用戶帶來了一定的不便,但是卻給GraphX的優化,提供便利和空間。
參考Graphx的Pregel代碼,對一個大圖,目前最佳的實踐是:
var g=...
var prevG: Graph[VD, ED] = null
while(...){
prevG = g
g = g.(………………)
g.cache()
prevG.unpersistVertices(blocking=false)
prevG.edges.unpersist(blocking=false)
}
大體之意,就是根據GraphX中graph的不變性,對g做了操作并賦回給g之后,g已經不是原來的g了,而且會在下一輪迭代使用,所以必須cache。另外,你必須先用prevG,保留住對原來的圖的引用,并在新圖產生之后,快速的將舊圖徹底的釋放掉。否則一個大圖,幾輪迭代下來,就會有內存泄漏的問題,很快耗光作業內存。
mrTriplets的全稱是mapReduceTriplets,它是GraphX中最核心和強大的一個接口。Pregel也基于它而來,所以對它的優化,能很大程度上影響整個GraphX的性能。
mrTriplets運算符的簡化定義是:
def mapReduceTriplets[A](
map: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)],
reduce: (A, A) => A)
: VertexRDD[A]
它的計算過程如下:
map:應用于每一個triplet上,生成一個或者多個消息, 消息以triplet關聯的兩個頂點中的任意一個或兩個為目標頂點
reduce:應用于每一個Vertex上,把發送給每一個頂點的消息合并起來
mrTriplets最后返回的是一個VertexRDD[A], 它包含了每一個頂點聚合之后的消息(類型為A), 沒有接收到消息的頂點不會包含在返回的VertexRDD中。
在最近的版本,GraphX針對它進行了如下幾個優化,這些優化,對于Pregel以及所有上層算法工具包的性能,都有著重大的影響。其中包括:
Caching for Iterative mrTriplets & Incremental Updates for Iterative mrTriplets
在很多圖分析算法中,不同點的收斂速度變化很大。在迭代的后期,只有很少的點會有更新。因此對于沒有更新的點,下一次mrTriplets計算時EdgeRDD無需更新相應點值的本地緩存,能夠大幅降低通信開銷。
Indexing Active Edges
沒有更新的頂點在下一輪迭代時就不需要向鄰居重新發送消息。因此mrTriplets遍歷邊時,如果一條邊的鄰居點值在上一輪迭代時沒有更新,可以直接跳過,避免了大量無用的計算和通信。
Join Elimination
一個triplet是由一條邊和其兩個鄰居點組成的三元組,操作triplet的map函數常常只需訪問其兩個鄰居點值中的一個。例如在PageRank計算中,一個點值的更新只和其源頂點的值有關,而其所指向的目的頂點的值無關。那么在mrTriplets計算中,就不需要VertexRDD和EdgeRDD的3-way join,而只需要2-way join。
所有的這些優化,都使得GraphX的性能,逐漸逼近GraphLab。雖然還有一定的差距,但是一體化的流水線服務,和豐富的編程接口,可以彌補性能的稍微差距。
Graphx中的Pregel接口,并不嚴格遵循Pregel的模型,它是一個參考GAS改進的Pregel模型。定義如下:
def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)(
vprog: (VertexID, VD, A) => VD,
sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexID,A)],
mergeMsg: (A, A) => A)
: Graph[VD, ED]
這種基于mrTrilets方法的Pregel模型,和標準的Pregel的最大區別是,它的第2段參數體,接受的是3個函數參數,而不接受messageList。它不會在單個頂點上進行消息遍歷,而是會將頂點的多個ghost副本收到的消息聚合后,發送給master副本,再使用vprog函數來更新點值。消息的接收和發送,都是被自動并行化處理的,無需擔心超級節點的問題。
常見的代碼模板如下所示:
//更新頂點
vprog(vid: Long, vert: Vertex, msg: Double): Vertex = {
v.score = msg + (1 - ALPHA) * v.weight
}
//發送消息
sendMsg(edgeTriplet: EdgeTriplet[…]): Iterator[(Long, Double)]
(destId, ALPHA * edgeTriplet.srcAttr.score * edgeTriplet.attr.weight)
}
//合并消息
mergeMsg(v1: Double, v2: Double): Double = {
v1+v2
}
可以看到,GraphX設計這個模型的用意。它綜合了Pregel和GAS兩者的優點,即接口相對簡單,又保證性能,可以應對點分割的圖存儲模式,勝任符合冪律分布的自然圖的大型計算。另外值得注意的是,官方的Pregel版本是最簡單的一個版本,對于復雜的業務場景,根據這個版本擴展一個定制的Pregel,是很常見的做法。
GraphX也提供了一套圖算法,方便用戶對圖進行分析。目前最新版本,已經支持PageRank,數三角形,最大連通圖,最短路徑等6種經典的圖算法,這些算法的代碼實現,目的和重點在于通用性。如果要獲得最佳性能,可以參考其實現,進行修改和擴展,可以滿足業務需求。另外研讀這些代碼,也是理解GraphX編程的Best Practice的好方法,建議有興趣深入研究分布式圖算法開發的同學都通讀一遍。
基本上,所有的關系,都可以從圖的角度來看待和處理,但是到底一個關系的價值多大?健康與否?適合用于什么場景?很多時候是靠運營和產品憑感覺來判斷和評估。如何將各種圖的指標精細化,規范化,對于產品和運營的構思進行數據上的預研指導,提供科學決策的依據,是圖譜體檢平臺設計的初衷和出發點。
基于這樣的出發點,借助GraphX豐富的接口和工具包,針對淘寶內部林林總總的圖業務需求, 我們開發一個圖譜體檢平臺。目前主要進行下列指標的檢查:
度分布
度分布是一個圖最基礎的指標,也是非常重要的一個指標。度分布檢測的目的,主要是了解圖中"超級節點"的個數和規模,以及所有節點度的分布曲線。超級節點的存在,對各種傳播算法,都會有重大的影響,不論是正面助力還是反面的阻力,所以要預先對于這些數據量有個預估。借助GraphX的最基本的圖信息接口:degrees: VertexRDD[Int],包括inDegrees和outDegrees,這個指標可以輕松地計算出來,并進行各種各樣的統計。
二跳鄰居數
對于大部分社交關系來說,只獲得一跳的度分布是遠遠不夠的,另一個重要的指標是二跳鄰居數。例如秘密App中,好友的好友的秘密,傳播的范圍更廣,信息量更豐富。因此二跳鄰居數的統計,是圖譜體檢中很重要的一個指標。二跳鄰居的計算GraphX沒有給出現成的接口,需要自己設計和開發。目前使用的方法是:
第一次遍歷,所有點往鄰居點傳播一個帶自身Id,生命值為2的消息
第二次遍歷,所有點將收到的消息,往鄰居點再轉發一次,生命值為1
最終統計所有點上,接收到的生命值為1的Id,并進行分組匯總,得到所有點的二跳鄰居
值得注意的是,進行這個計算之前,需要借助度分布,將圖中的超級節點去掉,不納入二跳鄰居數的計算。否則這些超級節點一來會出現在第一輪傳播后,收到過多的消息而爆掉,二來它們參與計算,會影響和它們有一跳鄰居關系的頂點,導致它們不能得到真正有效的二跳鄰居數。所以必須先篩選掉。
連通圖
檢測連通圖的目的,是弄清一個圖有幾個連通部分,以及每個連通部分有多少頂點。這樣可以將一個大圖分割為多個小圖,并去掉零碎的連通部分,從而可以在多個小子圖上,進行更加精細的操作。目前GraphX提供了ConnectedComponents和StronglyConnectedComponents算法,使用它們可以快速的計算出相應的連通圖。
連通圖可以進一步演化,變成社區發現算法,而該算法優劣的評判標準之一,是計算模塊的Q值,來查看所謂的modularity情況。但是GraphX中還是沒有對于Q值計算的函數,我們已經實現了一個,后續會將這個實現提交到社區。
更多的指標,例如Triangle Count和K-Core,無論是借助GraphX已有的函數,還是自己從頭開發,都陸續在進行中。目前這個圖譜體檢平臺已經初具規模,通過平臺的建立和推廣,圖相關的產品和業務,逐漸走上“無數據,不討論,用指標來預估效果”的數據化運營之路,有效提高溝通效率,為各種圖相關的業務開發走上科學化和系統化之路做好準備。
在圖譜體檢平臺的基礎上,我們可以了解到各種各樣關系的特點。不同的關系,都會有自己的強項和弱項,例如有些關系圖譜連通性好些,而有些關系圖譜的社交性好些,所以往往我們需要使用關系A來豐富關系B。為此,在圖譜體檢平臺之上,借助GraphX,我們開發了一個多圖合并工具,提供類似于圖的并集的概念,可以快速的對指定的2個不同關系圖譜,進行合并,產生一個新的關系圖譜。
以用基于A關系的圖來擴充基于B關系的圖,生成擴充圖C為例,融合算法基本思路如下:
若圖B中某邊的兩個頂點都在圖A中,則將該邊加入C圖(如BD邊)
若圖B中某邊的一個頂點在圖A中,另外一個頂點不在,則將該邊和另一頂點都加上(如CE邊和E點)
若圖A中某邊的兩個頂點都不在圖B中,則舍棄這條邊和頂點(如EF邊)
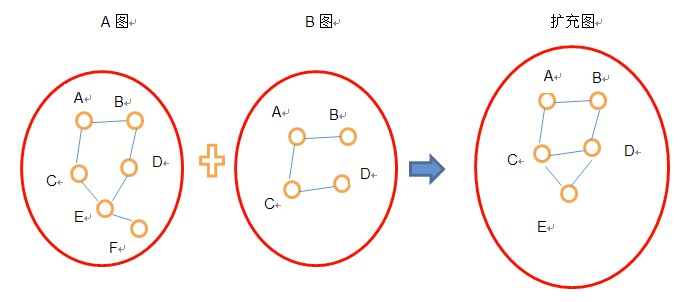
使用GraphX的outerJoinVertices等圖運算符,可以很簡單地完成上述的操作。另外,在考慮圖合并的時候,也可以考慮給不同的圖的邊加上不同的權重,綜合考慮點之間的不同關系的重要性。新產生的圖,會再進行一輪圖譜體檢,通過前后三個圖各個體檢指標的對比,可以對于業務上線之后效果有個預估和判斷。如果不符合期望,可以嘗試重新選擇擴充方案。
加權網絡上的能量傳播是經典的圖模型之一, 可用于用戶信譽度預測。模型的思路是:物以類聚,人以群分。常和信譽度高的用戶進行交易的,信譽度自然較高,常和信譽度差的用戶有業務來往的,信譽度自然較低。模型不復雜,但淘寶全網有上億的用戶點和幾十億關系邊,要對如此規模的巨型圖進行能量傳播,并對邊的權重進行精細的調節,對圖計算框架的性能和功能都是巨大的考驗。借助GraphX,我們在這兩點之間取得了平衡,成功實現了該模型。
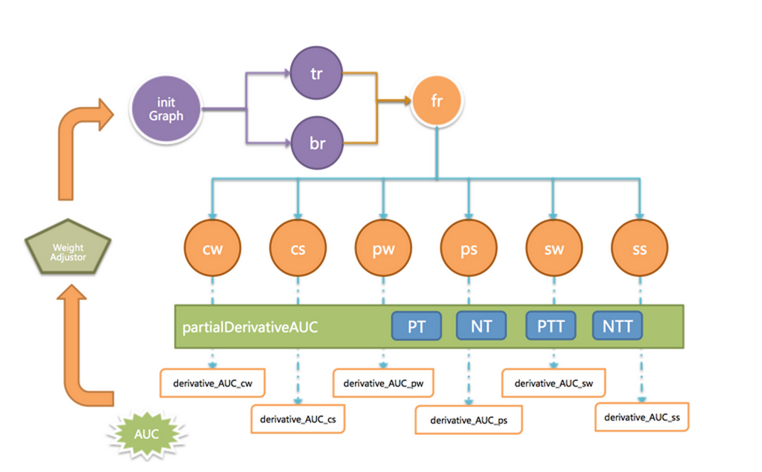
流程如圖4,先生成以用戶為點、買賣關系為邊的巨型圖initGraph,對選出種子用戶,分別賦予相同的初始正負能量值(TrustRank & BadRank),然后進行兩輪隨機游走,一輪好種子傳播正能量(tr),一輪壞種子傳播負能量(br),然后正負能量相減得到finalRank,根據finalRank判斷用戶的好壞。邊的初始傳播強度是0.85,這時AUC很低,需要再給每條邊,帶上一個由多個特征(交易次數,金額……)組成的組合權重。每個特征,都有不同的獨立權重和偏移量。通過使用partialDerivativeAUC方法,在訓練集上計算AUC,然后對AUC求偏導,得到每個關系維度的獨立權重和偏移量,生成新的權重調節器(WeightAdjustor),對圖上所有邊上的權重更新,然后再進行新一輪大迭代,這樣一直到AUC穩定時,終止計算。
在接近全量的數據上進行3輪大迭代,每輪2+6次Pregel,每次Pregel大約30次小迭代后,最終的AUC從0.6提升到0.9,達到了不錯的用戶預測準確率。訓練時長在6個小時左右,無論在性能還是準確率上,都超越業務方的期望。
經過半年多的嘗試,對于GraphX可以勝任的圖計算的規模和性能,目前我們都已經心中有數。之前一些想做,但因為沒有足夠的計算能力而不能實現的圖模型,現已經不是問題。我們將會進一步將越來越多的圖模型,在GraphX上實現。
這些模型應用于用戶網絡的社區發現、用戶影響力、能量傳播、標簽傳播等,可以提升用戶粘性和活躍度;而應用到推薦領域的標簽推理,人群劃分、年齡段預測、商品交易時序跳轉,則可以提升推薦的豐富度和準確性。復雜網絡和圖計算的天地廣闊無垠,有更多的未知等待我們去探索和實踐,借助Spark GraphX,未來我們可以迎接更大挑戰。
“Spark GraphX怎么使用”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。