您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“python模擬邏輯斯蒂回歸模型及最大熵模型舉例分析”,在日常操作中,相信很多人在python模擬邏輯斯蒂回歸模型及最大熵模型舉例分析問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”python模擬邏輯斯蒂回歸模型及最大熵模型舉例分析”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
思想:用了新的回歸函數y = 1/( exp(-x) ),其中x為分類函數,即w1*x1 + w2*x2 + ······ = 0。對于每一條樣本數據,我們計算一次y,并求出誤差△y;然后對權重向量w進行更新,更新策略為w = w + α*△y*x[i]' 其中α為學習率,△y為當前訓練數據的誤差,x[i]'為當前訓練數據的轉置;如此訓返往復。
這個例子中是對次數加了限制,也可以對誤差大小加以限制。
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
# data
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
# print(data)
return data[:, :2], data[:, -1]
class LogisticReressionClassifier:
def __init__(self, max_iter=200, learning_rate=0.01):
self.max_iter = max_iter # 對整個數據的最大訓練次數
self.learning_rate = learning_rate # 學習率
def sigmoid(self, x): # 回歸模型
return 1 / (1 + exp(-x))
# 對數據進行了整理,對原來的每行兩列添加了一列,
# 因為我們的線性分類器:w1*x1 + w2*x2 + b*1.0
# 所以將原來的(x1, x2,)擴充為(x1, x2, 1.0)
def data_matrix(self, X):
data_mat = []
for d in X:
data_mat.append([1.0, *d])
return data_mat
def fit(self, X, y):
data_mat = self.data_matrix(X) # 處理訓練數據
# 生成權重數組
# n行一列零數組,行數為data_mat[0]的長度
# 這里也就是我們的 w0,w1,w2
self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)
for iter_ in range(self.max_iter):
for i in range(len(X)): # 對每條X進行遍歷
# dot函數返回數組的點乘,也就是矩陣乘法:一行乘一列
# 在這里就是將 向量w*向量x 傳入回歸模型
# 返回訓練值
result = self.sigmoid(np.dot(data_mat[i], self.weights))
error = y[i] - result # 誤差
# transpose是轉置函數。改變權值
# w = w + 學習率*誤差*向量x
self.weights += self.learning_rate * error * np.transpose([data_mat[i]])
print('邏輯斯諦回歸模型訓練完成(learning_rate={},max_iter={})'.format(
self.learning_rate, self.max_iter))
def score(self, X_test, y_test):
right = 0
X_test = self.data_matrix(X_test)
for x, y in zip(X_test, y_test):
result = np.dot(x, self.weights)
if (result > 0 and y == 1) or (result < 0 and y == 0):
right += 1
return right / len(X_test)
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
lr_clf = LogisticReressionClassifier()
lr_clf.fit(X_train, y_train)
print("評分:")
print(lr_clf.score(X_test, y_test))
x_points = np.arange(4, 8)
# 原擬合函數為: w1*x1 + w2*x2 + b = 0
# 即 w1*x + w2*y + w0 = 0
y_ = -(lr_clf.weights[1]*x_points + lr_clf.weights[0])/lr_clf.weights[2]
plt.plot(x_points, y_)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.legend()
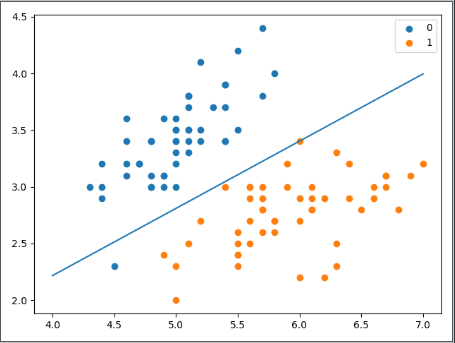
plt.show()結果如下:
邏輯斯諦回歸模型訓練完成(learning_rate=0.01,max_iter=200) 評分: 1.0
from math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
def create_data():
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['label'] = iris.target
df.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
data = np.array(df.iloc[:100, [0, 1, -1]])
# print(data)
return data[:, :2], data[:, -1]
X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)
clf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
print("socre:{}".format(clf.score(X_test, y_test)))
print(clf.coef_, clf.intercept_)
x_points = np.arange(4, 8)
y_ = -(clf.coef_[0][0]*x_points + clf.intercept_)/clf.coef_[0][1]
plt.plot(x_points, y_)
plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0')
plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
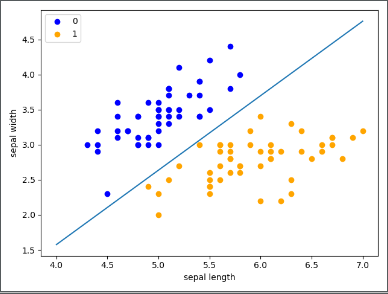
plt.show()結果:
socre:1.0 [[ 2.72989376 -2.5726044 ]] [-6.86599549]
最大熵原理:在滿足約束條件的模型集合中選取熵最大的模型。
思想比較簡單,但公式太多,結合課本公式使用更佳
import math
from copy import deepcopy
# 深復制:將被復制的對象完全復制一份
# 淺復制:將被復制的對象打一個標簽,兩者改變其一,另一個隨著改變
class MaxEntropy:
def __init__(self, EPS=0.005): # 參數為收斂條件
self._samples = [] # 存儲我們的訓練數據
self._Y = set() # 標簽集合,相當于去重后的y
self._numXY = {} # key為(x,y),value為出現次數
self._N = 0 # 樣本數
self._Ep_ = [] # 樣本分布的特征期望值
self._xyID = {} # key記錄(x,y),value記錄id號
self._n = 0 # 所有特征鍵值(x,y)的個數
self._C = 0 # 最大特征數
self._IDxy = {} # key為ID,value為對應的(x,y)
self._w = [] #存我們的w系數
self._EPS = EPS # 收斂條件
self._lastw = [] # 上一次w參數值
def loadData(self, dataset):
self._samples = deepcopy(dataset)
for items in self._samples:
y = items[0]
X = items[1:]
self._Y.add(y) # 集合中y若已存在則會自動忽略
for x in X:
if (x, y) in self._numXY:
self._numXY[(x, y)] += 1
else:
self._numXY[(x, y)] = 1
self._N = len(self._samples)
self._n = len(self._numXY)
self._C = max([len(sample) - 1 for sample in self._samples])
self._w = [0] * self._n # w參數初始化為n個0,其中n為所有特征值數
self._lastw = self._w[:]
self._Ep_ = [0] * self._n
# 計算特征函數fi關于經驗分布的期望
# 其中i對應第幾條
# xy對應(x, y)
for i, xy in enumerate(self._numXY):
self._Ep_[i] = self._numXY[xy] / self._N
self._xyID[xy] = i
self._IDxy[i] = xy
def _Zx(self, X): # 計算每個Z(x)值。其中Z(x)為規范化因子。
zx = 0
for y in self._Y:
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
zx += math.exp(ss)
return zx
def _model_pyx(self, y, X): # 計算每個P(y|x)
zx = self._Zx(X)
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
pyx = math.exp(ss) / zx
return pyx
def _model_ep(self, index): # 計算特征函數fi關于模型的期望
x, y = self._IDxy[index]
ep = 0
for sample in self._samples:
if x not in sample:
continue
pyx = self._model_pyx(y, sample)
ep += pyx / self._N
return ep
def _convergence(self): # 判斷是否全部收斂
for last, now in zip(self._lastw, self._w):
if abs(last - now) >= self._EPS:
return False
return True
def predict(self, X): # 計算預測概率
Z = self._Zx(X)
result = {}
for y in self._Y:
ss = 0
for x in X:
if (x, y) in self._numXY:
ss += self._w[self._xyID[(x, y)]]
pyx = math.exp(ss) / Z
result[y] = pyx
return result
def train(self, maxiter=1000): # 訓練數據
for loop in range(maxiter): # 最大訓練次數
self._lastw = self._w[:]
for i in range(self._n):
ep = self._model_ep(i) # 計算第i個特征的模型期望
self._w[i] += math.log(self._Ep_[i] / ep) / self._C # 更新參數
if self._convergence(): # 判斷是否收斂
break
dataset = [['no', 'sunny', 'hot', 'high', 'FALSE'],
['no', 'sunny', 'hot', 'high', 'TRUE'],
['yes', 'overcast', 'hot', 'high', 'FALSE'],
['yes', 'rainy', 'mild', 'high', 'FALSE'],
['yes', 'rainy', 'cool', 'normal', 'FALSE'],
['no', 'rainy', 'cool', 'normal', 'TRUE'],
['yes', 'overcast', 'cool', 'normal', 'TRUE'],
['no', 'sunny', 'mild', 'high', 'FALSE'],
['yes', 'sunny', 'cool', 'normal', 'FALSE'],
['yes', 'rainy', 'mild', 'normal', 'FALSE'],
['yes', 'sunny', 'mild', 'normal', 'TRUE'],
['yes', 'overcast', 'mild', 'high', 'TRUE'],
['yes', 'overcast', 'hot', 'normal', 'FALSE'],
['no', 'rainy', 'mild', 'high', 'TRUE']]
maxent = MaxEntropy()
x = ['overcast', 'mild', 'high', 'FALSE']
maxent.loadData(dataset)
maxent.train()
print('predict:', maxent.predict(x))結果:
predict: {'yes': 0.9999971802186581, 'no': 2.819781341881656e-06}到此,關于“python模擬邏輯斯蒂回歸模型及最大熵模型舉例分析”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。