數據結構之堆（Heap）的實現

  堆數據結構是一種數組對象，它可以被視為一棵完全二叉樹結構，所以堆也叫做二叉堆。

• 二叉堆滿足二個特性：

  1．父結點的鍵值總是大于或等于（小于或等于）任何一個子節點的鍵值。

  2．每個結點的左子樹和右子樹都是一個二叉堆（都是最大堆或最小堆）。

  當父結點的鍵值總是大于或等于任何一個子節點的鍵值時為最大堆。當父結點的鍵值總是小于或等于   任何一個子節點的鍵值時為最小堆。

  最大堆和最小堆是堆數據結構的重點。堆排序中使用特別的多。

•  堆的存儲一般是用一個數組實現的，當然也可以用鏈式存儲，但是特別麻煩。

  如下我們給出一個數組：

  int* Arry={10,16,18,12,11,13,15,17,14,19};

  現在我們要根據這個數組來建一個不是真正意義上的堆。

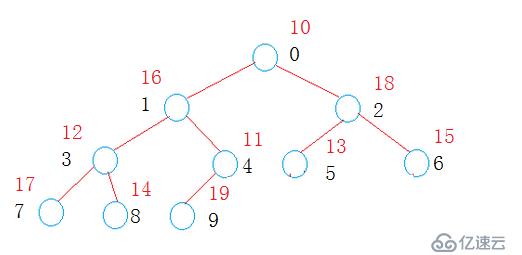
 現在的堆并不是真正的堆，它不滿足最大堆或者最小堆，所以它是無意義的，我們要調整這個“堆”讓它變成最大堆或者最小堆，這一步操作就是調整堆。

 調整堆：首先我們要明確調整堆的目的就是讓整棵樹中的雙親節點都大于孩子節點（這里以最大堆為例），所以我們要從葉子結點開始調整，直到調整到根節點結束，可能調整好這棵樹后，子樹又不符合最大堆規則，轉而調整子樹，所以我們把這種方式叫下調（AdjustDown）

#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;

template<class T>
struct Less
{
	bool operator()(const T& l, const T& r)
	{
		return l < r;
	}
};


template<class T>
struct Greater
{
	bool operator()(const T& l, const T& r)
	{
		return l > r;
	}
};

template<class T,template<class> class Continer = Greater>//默認為大堆
class Heap
{
public:
	Heap(){};
	Heap(const T* a, size_t size, Continer<T> con);
	Heap(const vector<T>& v);
	void Push(const T& x);
	void Pop();
	T& GetTop();
	bool Empty();
	size_t Size();
	void HeapSort(T* a, size_t size);
protected:
	void _AdjustDown(size_t parent);
	void _AdjustUp(size_t child);
protected:
	vector<T> _a;
	Continer<T> _con;
};

template<class T, template<class> class Continer = Less>
Heap<T,Continer>::Heap(const T* a,size_t size ,Continer<T> con)
{
	_a.reserve(size);

	for (size_t i = 0; i < size; ++i)
	{
		_a.push_back(a[i]);
	}

	//建堆
	for (int i = (_a.size() - 2) / 2; i >= 0; i--)
		//從第一個非葉子結點開始下調，葉子結點可以看作是一個大堆或小堆
	{

		_AdjustDown(i);
	}
}
template<class T, template<class> class Continer = Less>
void Heap<T,Continer>::_AdjustDown(size_t parent)
{
	size_t child = parent * 2 + 1;
	size_t size = _a.size();
	while (child < size)
	{
		if (child + 1 < size&&_con(_a[child+1],_a[child]))
			//注意這必須是child+1更大或更小，所以把child+1放在前面
			++child;
		if (_con(_a[child],_a[parent]))
		{
			swap(_a[parent], _a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

  在這里是使用的類去封裝堆結構，并且用了仿函數的方式去復用最大堆和最小堆的代碼。在這里默認把堆調整為最大堆。

 以下是堆的調用：

	int array[] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19 };
	size_t size = sizeof(array) / sizeof(int);
	Greater<int> ger;
	Heap<int,Greater> h(array, size, ger);//因為默認為大頂堆，所以可以省略Greater

  我們的調整堆的操作是從二叉樹的第一個非葉子結點開始調整。有的讀者會問為什么不從最后一個結點調整呢？因為所有葉子結點我們都可以看作一個最大堆或者最小堆，我們完全不需要去調整。

 要調整為一個最小堆的話只要修改一下調用即可：

	int array[] = { 10, 16, 18, 12, 11, 13, 15, 17, 14, 19 };
	size_t size = sizeof(array) / sizeof(int);
	Less<int> les;
	Heap<int，Less> h2(array, size, les);

• 向一個最大堆（最小堆中插入一個數據），讓堆仍為最大堆（最小堆）。

   Push操作：向堆中插入一個數據，也就是往數組中插入一個數據，插入數據以后一般都不是最大堆（最小堆），我們得去調整。

 上調（AdjustUP）：把新插入的結點大于（小于）雙親節點則往上調，直到滿足最大堆（最小堆）。

template<class T, template<class> class Continer = Less>
void Heap<T, Continer>::Push(const T& x)
{
	_a.push_back(x);
	_AdjustUp(_a.size() - 1);
}
template<class T, template<class> class Continer = Less>
void Heap<T, Continer>::_AdjustUp(size_t child)
{
	size_t parent = (child - 1) / 2;
	while (child > 0)
	{
		if (_con(_a[child] , _a[parent]))
		{
			swap(_a[child], _a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
			break;
	}
}

•   刪除最大堆（最小堆）中的根結點。

  我們把根節點刪除以后剩下的結點就不構成一棵樹結構了，所以我們可以換一種思路讓堆保持原來的結構。

  方法就是把根節點和最后一個結點交換，刪除最后一個結點，這樣就不會破環結構了。

  把結點刪除后，堆肯定不滿足最大堆（最小堆）了，所以我們還要調整堆。這次我們要從根節點往葉子結點調，這樣很快，因為原來的堆根節點的左右子樹都已經滿足大小堆了。利用下調來調整：

template<class T, template<class> class Continer = Less>
void Heap<T, Continer>::Pop()
{
	assert(!_a.empty());
	size_t size = _a.size();
	swap(_a[0], _a[size - 1]);
	_a.pop_back();
	_AdjustDown(0);
}

  堆和棧是計算機內存最常用的結構。

  有了最大堆和最小堆，我們可以利用他們的特性來實現堆排序。