您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章給大家介紹 HTML5 中怎么實現一個3D網絡拓撲樹,內容非常詳細,感興趣的小伙伴們可以參考借鑒,希望對大家能有所幫助。
1. 創建一個樹狀結構
有了解過HT for Web的朋友,對樹狀結構數據的創建應該都不陌生,在這里我就不做深入的探討了。樹狀結構數據的創建很簡單,在這里為了讓代碼更簡潔,我封裝了三個方法來創建樹狀結構數據,具體代碼如下:
/**
* 創建連線
* @param {ht.DataModel} dataModel - 數據容器
* @param {ht.Node} source - 起點
* @param {ht.Node} target - 終點
*/
function createEdge(dataModel, source, target) {
// 創建連線,鏈接父親節點及孩子節點
var edge = new ht.Edge();
edge.setSource(source);
edge.setTarget(target);
dataModel.add(edge);
}
/**
* 創建節點對象
* @param {ht.DataModel} dataModel - 數據容器
* @param {ht.Node} [parent] - 父親節點
* @returns {ht.Node} 節點對象
*/
function createNode(dataModel, parent) {
var node = new ht.Node();
if (parent) {
// 設置父親節點
node.setParent(parent);
createEdge(dataModel, parent, node);
}
// 添加到數據容器中
dataModel.add(node);
return node;
}
/**
* 創建結構樹
* @param {ht.DataModel} dataModel - 數據容器
* @param {ht.Node} parent - 父親節點
* @param {Number} level - 深度
* @param {Array} count - 每層節點個數
* @param {function(ht.Node, Number, Number)} callback - 回調函數(節點對象,節點對應的層級,節點在層級中的編號)
*/
function createTreeNodes(dataModel, parent, level, count, callback) {
level--;
var num = (typeof count === 'number' ? count : count[level]);
while (num--) {
var node = createNode(dataModel, parent);
// 調用回調函數,用戶可以在回調里面設置節點相關屬性
callback(node, level, num);
if (level === 0) continue;
// 遞歸調用創建孩子節點
createTreeNodes(dataModel, node, level, count, callback);
}
}
嘿嘿,代碼寫得可能有些復雜了,簡單的做法就是嵌套幾個for循環來創建樹狀結構數據,在這里我就不多說了,接下來我們來探究第二個問題。
2. 在2D拓撲下模擬3D樹狀結構每層的半徑計算
在3D下的樹狀結構體***的問題就在于,每個節點的層次及每層節點圍繞其父親節點的半徑計算。現在樹狀結構數據已經有了,那么接下來就該開始計算半徑了,我們從兩層樹狀結構開始推算:
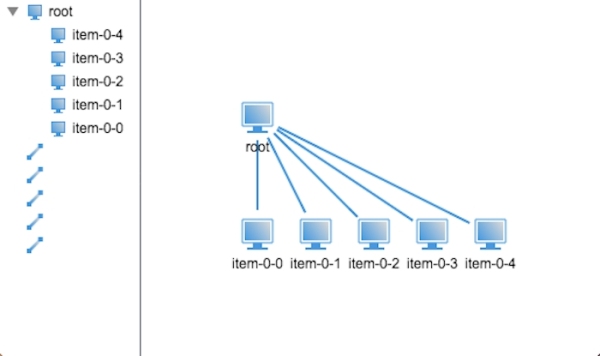
我現在先創建了兩層的樹狀結構,所有的子節點是一字排開,并沒有環繞其父親節點,那么我們該如何去確定這些孩子節點的位置呢?
首先我們得知道,每個末端節點都有一圈屬于自己的領域,不然節點與節點之間將會存在重疊的情況,所以在這里,我們假定末端節點的領域半徑為25,那 么兩個相鄰節點之間的最短距離將是兩倍的節點領域半徑,也就是50,而這些末端節點將均勻地圍繞在其父親節點四周,那么相鄰兩個節點的張角就可以確認出 來,有了張角,有了兩點間的距離,那么節點繞其父親節點的最短半徑也就能計算出來了,假設張角為a,兩點間最小距離為b,那么最小半徑r的計算公式為:
r = b / 2 / sin(a / 2);
那么接下來我么就來布局下這個樹,代碼是這樣寫的:
/**
* 布局樹
* @param {ht.Node} root - 根節點
* @param {Number} [minR] - 末端節點的最小半徑
*/
function layout(root, minR) {
// 設置默認半徑
minR = (minR == null ? 25 : minR);
// 獲取到所有的孩子節點對象數組
var children = root.getChildren().toArray();
// 獲取孩子節點個數
var len = children.length;
// 計算張角
var degree = Math.PI * 2 / len;
// 根據三角函數計算繞父親節點的半徑
var sin = Math.sin(degree / 2),
r = minR / sin;
// 獲取父親節點的位置坐標
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根據三角函數計算每個節點相對于父親節點的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 設置孩子節點的位置坐標
child.p(x + rootPosition.x, y + rootPosition.y);
});
}
在代碼中,你會發現我將末端半徑默認設置為25了,如此,我們通過調用layout()方法就可以對結構樹進行布局了,其布局效果如下:
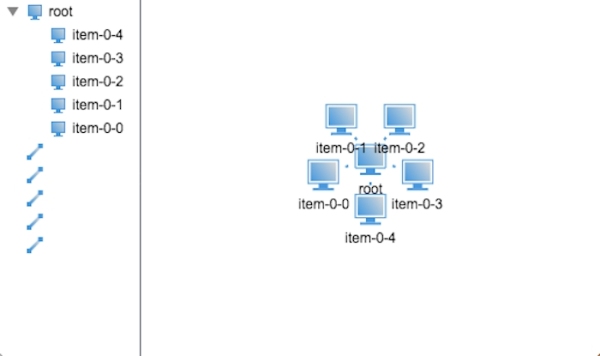
從效果圖可以看得出,末端節點的默認半徑并不是很理想,布局出來的效果連線都快看不到了,因此我們可以增加末端節點的默認半徑來解決布局太密的問題,如將默認半徑設置成40的效果圖如下:
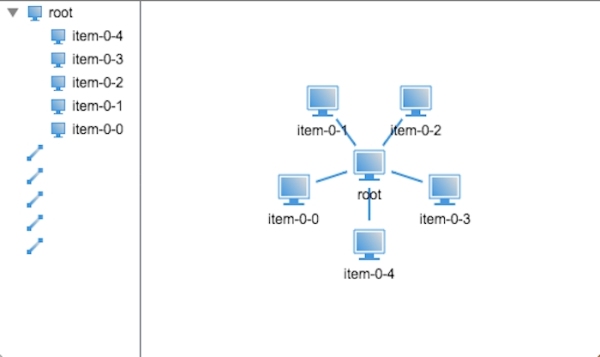
現在兩層的樹狀分布解決了,那么我們來看看三層的樹狀分布該如何處理。
將第二層和第三層看成一個整體,那么其實三層的樹狀結構跟兩層是一樣的,不同的是在處理第二層節點時,應該將其看做一個兩層的樹狀結構來處理,那么像這種規律的處理用遞歸***不過了,因此我們將代碼稍微該著下,在看看效果如何:
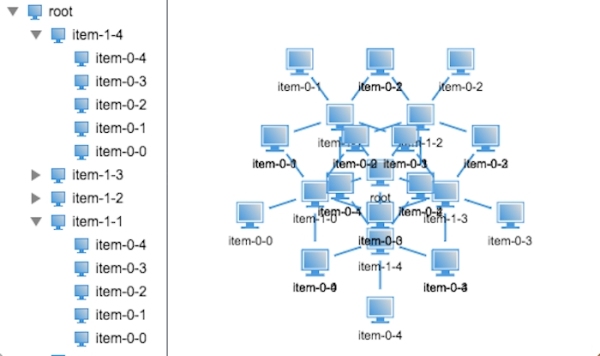
不行,節點都重疊在一起了,看來簡單的遞歸是不行的,那么具體的問題出在哪里呢?
仔細分析了下,發現父親節點的領域半徑是由其孩子節點的領域半徑決定的,因此在布局時需要知道自身節點的領域半徑,而且節點的位置取決于父親節點的領域半徑及位置信息,這樣一來就無法邊計算半徑邊布局節點位置了。
那么現在只能將半徑的計算和布局分開來,做兩步操作了,我們先來分析下節點半徑的計算:
首先需要明確最關鍵的條件,父親節點的半徑取決于其孩子節點的半徑,這個條件告訴我們,只能從下往上計算節點半徑,因此我們設計的遞歸函數必須是先遞歸后計算,廢話不多說,我們來看下具體的代碼實現:
/**
* 就按節點領域半徑
* @param {ht.Node} root - 根節點對象
* @param {Number} minR - 最小半徑
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端節點,則設置其半徑為最小半徑
if (!root.hasChildren()) {
root.a('radius', minR);
return;
}
// 遍歷孩子節點遞歸計算半徑
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 獲取孩子節點半徑
var radius = child0.a('radius');
// 計算子節點的1/2張角
var degree = Math.PI / children.size();
// 計算父親節點的半徑
var pRadius = radius / Math.sin(degree);
// 設置父親節點的半徑及其孩子節點的布局張角
root.a('radius', pRadius);
root.a('degree', degree * 2);
}
OK,半徑的計算解決了,那么接下來就該解決布局問題了,布局樹狀結構數據需要明確:孩子節點的坐標位置取決于其父親節點的坐標位置,因此布局的遞歸方式和計算半徑的遞歸方式不同,我們需要先布局父親節點再遞歸布局孩子節點,具體看看代碼吧:
/**
* 布局樹
* @param {ht.Node} root - 根節點
*/
function layout(root) {
// 獲取到所有的孩子節點對象數組
var children = root.getChildren().toArray();
// 獲取孩子節點個數
var len = children.length;
// 計算張角
var degree = root.a('degree');
// 根據三角函數計算繞父親節點的半徑
var r = root.a('radius');
// 獲取父親節點的位置坐標
var rootPosition = root.p();
children.forEach(function(child, index) {
// 根據三角函數計算每個節點相對于父親節點的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
y = c * r;
// 設置孩子節點的位置坐標
child.p(x + rootPosition.x, y + rootPosition.y);
// 遞歸調用布局孩子節點
layout(child);
});
}
代碼寫完了,接下來就是見證奇跡的時刻了,我們來看看效果圖吧:
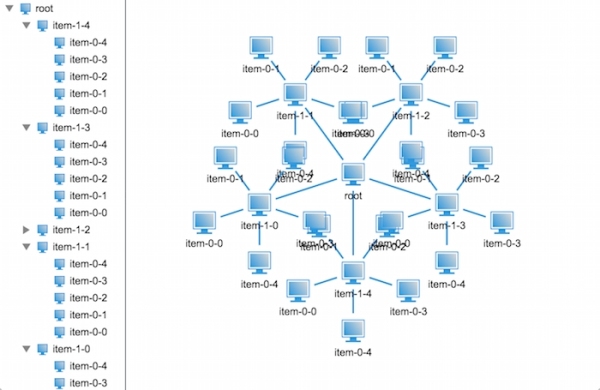
不對呀,代碼應該是沒問題的呀,為什么顯示出來的效果還是會重疊呢?不過仔細觀察我們可以發現相比上個版本的布局會好很多,至少這次只是末端節點重疊了,那么問題出在哪里呢?
不知道大家有沒有發現,排除節點自身的大小,倒數第二層節點與節點之間的領域是相切的,那么也就是說節點的半徑不僅和其孩子節點的半徑有關,還與其孫子節點的半徑有關,那我們把計算節點半徑的方法改造下,將孫子節點的半徑也考慮進去再看看效果如何,改造后的代碼如下:
/**
* 就按節點領域半徑
* @param {ht.Node} root - 根節點對象
* @param {Number} minR - 最小半徑
*/
function countRadius(root, minR) {
……
var child0 = root.getChildAt(0);
// 獲取孩子節點半徑
var radius = child0.a('radius');
var child00 = child0.getChildAt(0);
// 半徑加上孫子節點半徑,避免節點重疊
if (child00) radius += child00.a('radius');
……
}
下面就來看看效果吧~
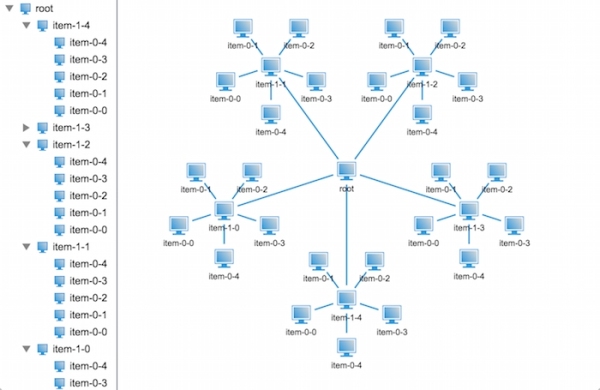
哈哈,看來我們分析對了,果然就不再重疊了,那我們來看看再多一層節點會是怎么樣的壯觀場景呢?

哦,NO!這不是我想看到的效果,又重疊了,好討厭。
不要著急,我們再來仔細分析分析下,在前面,我們提到過一個名詞——領域半徑,什么是領域半徑呢?很簡單,就是可以容納下自身及其所有孩子節點的最 小半徑,那么問題就來了,末端節點的領域半徑為我們指定的最小半徑,那么倒數第二層的領域半徑是多少呢?并不是我們前面計算出來的半徑,而應該加上末端節 點自身的領域半徑,因為它們之間存在著包含關系,子節點的領域必須包含于其父親節點的領域中,那我們在看看上圖,是不是感覺末端節點的領域被侵占了。那么 我們前面計算出來的半徑代表著什么呢?前面計算出來的半徑其實代表著孩子節點的布局半徑,在布局的時候是通過該半徑來布局的。
OK,那我們來總結下,節點的領域半徑是其下每層節點的布局半徑之和,而布局半徑需要根據其孩子節點個數及其領域半徑共同決定。
好了,我們現在知道問題的所在了,那么我們的代碼該如何去實現呢?接著往下看:
/**
* 就按節點領域半徑及布局半徑
* @param {ht.Node} root - 根節點對象
* @param {Number} minR - 最小半徑
*/
function countRadius(root, minR) {
minR = (minR == null ? 25 : minR);
// 若果是末端節點,則設置其布局半徑及領域半徑為最小半徑
if (!root.hasChildren()) {
root.a('radius', minR);
root.a('totalRadius', minR);
return;
}
// 遍歷孩子節點遞歸計算半徑
var children = root.getChildren();
children.each(function(child) {
countRadius(child, minR);
});
var child0 = root.getChildAt(0);
// 獲取孩子節點半徑
var radius = child0.a('radius'),
totalRadius = child0.a('totalRadius');
// 計算子節點的1/2張角
var degree = Math.PI / children.size();
// 計算父親節點的布局半徑
var pRadius = totalRadius / Math.sin(degree);
// 緩存父親節點的布局半徑
root.a('radius', pRadius);
// 緩存父親節點的領域半徑
root.a('totalRadius', pRadius + totalRadius);
// 緩存其孩子節點的布局張角
root.a('degree', degree * 2);
}
在代碼中我們將節點的領域半徑緩存起來,從下往上一層一層地疊加上去。接下來我們一起驗證其正確性:
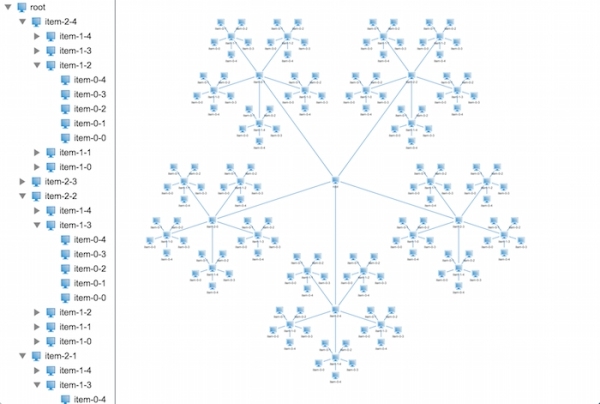
搞定,就是這樣子了,2D拓撲上面的布局搞定了,那么接下來該出動3D拓撲啦~
3. 加入z軸坐標,呈現3D下的樹狀結構
3D拓撲上面布局無非就是多加了一個坐標系,而且這個坐標系只是控制節點的高度而已,并不會影響到節點之間的重疊,所以接下來我們來改造下我們的程序,讓其能夠在3D上正常布局。
也不需要太大的改造,我們只需要修改下布局器并且將2D拓撲組件改成3D拓撲組件就可以了。
/**
* 布局樹
* @param {ht.Node} root - 根節點
*/
function layout(root) {
// 獲取到所有的孩子節點對象數組
var children = root.getChildren().toArray();
// 獲取孩子節點個數
var len = children.length;
// 計算張角
var degree = root.a('degree');
// 根據三角函數計算繞父親節點的半徑
var r = root.a('radius');
// 獲取父親節點的位置坐標
var rootPosition = root.p3();
children.forEach(function(child, index) {
// 根據三角函數計算每個節點相對于父親節點的偏移量
var s = Math.sin(degree * index),
c = Math.cos(degree * index),
x = s * r,
z = c * r;
// 設置孩子節點的位置坐標
child.p3(x + rootPosition[0], rootPosition[1] - 100, z + rootPosition[2]);
// 遞歸調用布局孩子節點
layout(child);
});
}
上面是改造成3D布局后的布局器代碼,你會發現和2D的布局器代碼就差一個坐標系的的計算,其他的都一樣,看下在3D上布局的效果:
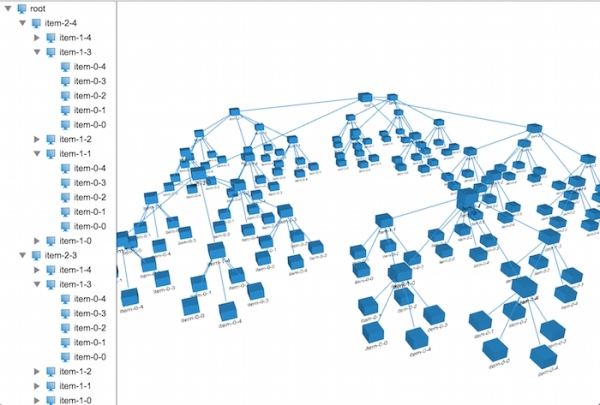
恩,有模有樣的了,在文章的開頭,我們可以看到每一層的節點都有不同的顏色及大小,這些都是比較簡單,在這里我就不做深入的講解,具體的代碼實現如下:
var level = 4,
size = (level + 1) * 20;
var root = createNode(dataModel);
root.setName('root');
root.p(100, 100);
root.s('shape3d', 'sphere');
root.s('shape3d.color', randomColor());
root.s3(size, size, size);
var colors = {},
sizes = {};
createTreeNodes(dataModel, root, level - 1, 5, function(data, level, num) {
if (!colors[level]) {
colors[level] = randomColor();
sizes[level] = (level + 1) * 20;
}
size = sizes[level];
data.setName('item-' + level + '-' + num);
// 設置節點形狀為球形
data.s('shape3d', 'sphere');
data.s('shape3d.color', colors[level]);
data.s3(size, size, size);
});
在這里引入了一個隨機生成顏色值的方法,對每一層隨機生成一種顏色,并將節點的形狀改成了球形,讓頁面看起來美觀些(其實很丑)。
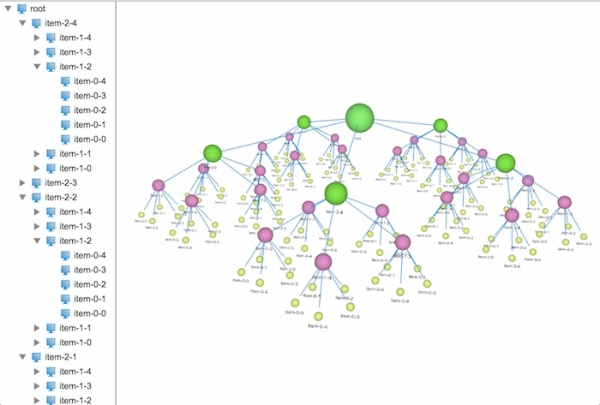
關于 HTML5 中怎么實現一個3D網絡拓撲樹就分享到這里了,希望以上內容可以對大家有一定的幫助,可以學到更多知識。如果覺得文章不錯,可以把它分享出去讓更多的人看到。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。