結合React源碼如何快速掌握優先隊列

這篇文章主要講解了“結合React源碼如何快速掌握優先隊列”，文中的講解內容簡單清晰，易于學習與理解，下面請大家跟著小編的思路慢慢深入，一起來研究和學習“結合React源碼如何快速掌握優先隊列”吧！

什么是優先隊列

• 優先隊列是數據結構中的基礎概念，與隊列先進先出(FIFO)的出隊順序不同的是 ，它的出隊順序與元素的優先級相關。

• 例如 React 的時間分片(React Fiber)，它將渲染任務分了優先級，出隊的順序與任務的“重要程度”存在關系，那么滿足這種情況的數據結構就是  優先隊列 。

優先隊列的操作

• 插入：在優先隊列中插入元素，并使隊列“有序”

• 刪除最大/最小值：刪除并返回最大/最小的元素，并使隊列“有序”

• 查找最大/最小關鍵字：查找最大/最小的值

優先隊列的實現比較

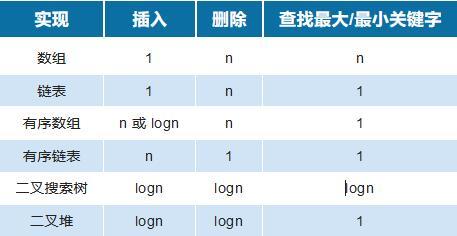
優先隊列可以由以上多種方式實現，而優先隊列的主要操作是插入和刪除，其中二叉搜索樹和二叉堆這兩項操作的時間復雜度均為 logn  ,但二叉樹在多次刪除之后容易導致樹的傾斜，同時查找成本也高于二叉堆，所以最終二叉堆是比較符合實現優先隊列的數據結構。

二叉堆

在二叉堆中數組中，要保證每個元素都小于(大于)或等于另外兩個特定位置的元素。例如下圖的樹中，父節點總是小于或等于子節點。

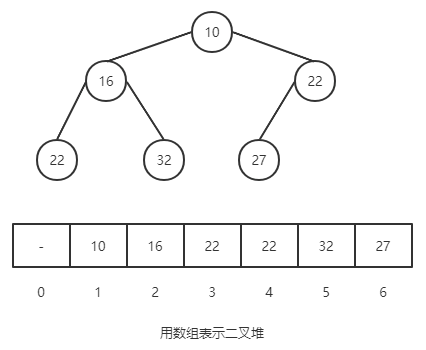
對于二叉堆有如下性質：

• 節點 k 的父節點下標為 k / 2(向下取整)

• 已某節點為根節點的子樹，該節點是這顆樹的極值

二叉堆的操作

插入

二叉堆的插入非常簡單，只需要在二叉堆的最后添加要插入的內容，并將其“上浮”到正確位置。

嘗試在上面的二叉堆中插入新元素 9，過程如下：

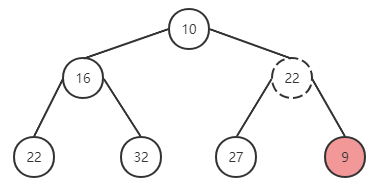
在尾部插入元素 9，與父節點進行對比，有序性被破壞，與父元素替換位置。

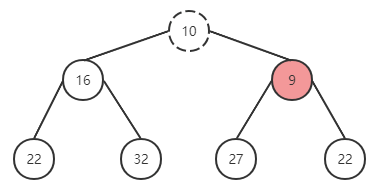
替換成功后，繼續上一輪操作，與父節點進行對比，仍然無法滿足有序性，繼續調換位置。

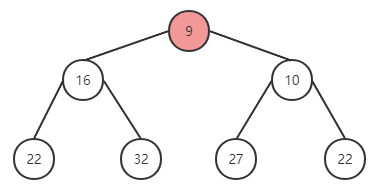
再次替換后符合。

程序框架

function push {   * 在堆尾部添加元素   * 執行上浮循環     * 與父元素對比大小，將較大的放在父節點位置    return minItem }

實現

function push(heap: Heap, node: Node): void {   const index = heap.length;   heap.push(node); // 在堆尾部添加元素   siftUp(heap, node, index); // 進行上浮操作 }  function siftUp(heap, node, i) {   let index = i;   while (true) {     const parentIndex = (index - 1) >>> 1; // 父節點位置： parentIndex = childIndex / 2     const parent = heap[parentIndex];     if (parent !== undefined && compare(parent, node) > 0) {       // The parent is larger. Swap positions.       heap[parentIndex] = node;       heap[index] = parent;       index = parentIndex;     } else {       // The parent is smaller. Exit.       return;     }   } }

刪除

取出根節點的值對比插入稍微復雜一點，歸納起來可以分為三步：

• 取出根節點的值

• 將最后一個元素與根節點進行替換，并刪除最后一個元素

• 下沉

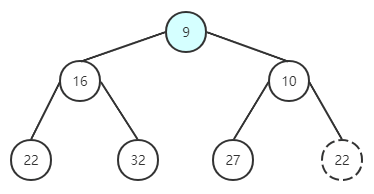
取出根節點。

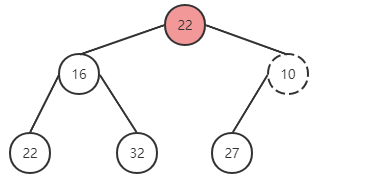
將最后一個元素與根節點調換，并刪除。對比發現有序性被破壞，進行對調。

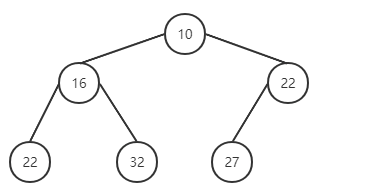
完成刪除。

程序框架

function pop {   * 設定 minItem 保存根節點   * 取出最后一個節點與根節點替換，并刪除最后一個節點   * 執行下沉循環     * 將根元素與左右子節點對比,挑選較小的與父節點替換位置    return minItem }

實現

export function pop(heap: Heap): Node | null {   const first = heap[0]; // 取出根節點   if (first !== undefined) {     const last = heap.pop(); // 取出最后一位元素，并刪除     if (last !== first) {       heap[0] = last; // 與根節點對調       siftDown(heap, last, 0); // 下沉     }     return first;   } else {     return null;   } }  function siftDown(heap, node, i) {   let index = i;   const length = heap.length;   while (index < length) {     const leftIndex = (index + 1) * 2 - 1;     const left = heap[leftIndex];     const rightIndex = leftIndex + 1;     const right = heap[rightIndex];      // If the left or right node is smaller, swap with the smaller of those.     // 尋找左右兒子較小的那一個替換     if (left !== undefined && compare(left, node) < 0) { //左子節點小于根節點       if (right !== undefined && compare(right, left) < 0) {         heap[index] = right;         heap[rightIndex] = node;         index = rightIndex;       } else {         heap[index] = left;         heap[leftIndex] = node;         index = leftIndex;       }     } else if (right !== undefined && compare(right, node) < 0) { // 左子節點大于根節點，右子節點小于根節點       heap[index] = right;       heap[rightIndex] = node;       index = rightIndex;     } else {       // Neither child is smaller. Exit.       return;     }   } }

以下是 react 源碼中 scheduler/src/SchedulerMinHeap.js 關于最小堆的完整實現：

/**  * Copyright (c) Facebook, Inc. and its affiliates.  *  * This source code is licensed under the MIT license found in the  * LICENSE file in the root directory of this source tree.  *  * @flow strict  */  // 定義最小堆極其元素，其中 sortIndex 為最小堆對比的 key，若 sortIndex 相同，則對比 id type Heap = Array<Node>; type Node = {|   id: number,   sortIndex: number, |};  // 入隊操作，在入隊完成之后進行“上浮” export function push(heap: Heap, node: Node): void {   const index = heap.length;   heap.push(node);   siftUp(heap, node, index); }  // 查找最大值 export function peek(heap: Heap): Node | null {   const first = heap[0];   return first === undefined ? null : first; }  // 刪除并返回最大值 export function pop(heap: Heap): Node | null {   const first = heap[0]; // 取出根節點（哨兵）   if (first !== undefined) {     const last = heap.pop(); // 取出最后一位元素，并刪除     if (last !== first) { // 頭尾并沒有對撞       heap[0] = last; // 與根節點對調       siftDown(heap, last, 0); // 下沉     }     return first;   } else {     return null;   } }  // 上浮，調整樹結構 function siftUp(heap, node, i) {   let index = i;   while (true) {     const parentIndex = (index - 1) >>> 1; // 父節點位置： parentIndex = childIndex / 2，此處使用位操作，右移一位     const parent = heap[parentIndex];     if (parent !== undefined && compare(parent, node) > 0) { // 對比父節點和子元素的大小       // The parent is larger. Swap positions.       heap[parentIndex] = node; // 若父節點較大，則更換位置       heap[index] = parent;       index = parentIndex;     } else {       // The parent is smaller. Exit.       return;     }   } }  // 下沉，調整樹結構 function siftDown(heap, node, i) {   let index = i;   const length = heap.length;   while (index < length) {     const leftIndex = (index + 1) * 2 - 1;     const left = heap[leftIndex];     const rightIndex = leftIndex + 1;     const right = heap[rightIndex];      // If the left or right node is smaller, swap with the smaller of those.     // 尋找左右兒子較小的那一個替換     if (left !== undefined && compare(left, node) < 0) {       if (right !== undefined && compare(right, left) < 0) { // 左子節點小于根節點         heap[index] = right;         heap[rightIndex] = node;         index = rightIndex;       } else {         heap[index] = left;         heap[leftIndex] = node;         index = leftIndex;       }     } else if (right !== undefined && compare(right, node) < 0) { // 左子節點大于根節點，右子節點小于根節點       heap[index] = right;       heap[rightIndex] = node;       index = rightIndex;     } else {       // Neither child is smaller. Exit.       return;     }   } }  function compare(a, b) {   // Compare sort index first, then task id.   const diff = a.sortIndex - b.sortIndex;   return diff !== 0 ? diff : a.id - b.id; }

堆排序

利用最大/最小堆的特性，我們很容易就能實現對數組的排序，重復執行 pop 就能進行升序排列，如果要降序，使用最大堆即可，該操作時間復雜度為 nlogn  。

多叉堆

為了追求更優的時間復雜度，我們可以將二叉堆改為多叉堆實現，下圖為一個三叉堆：

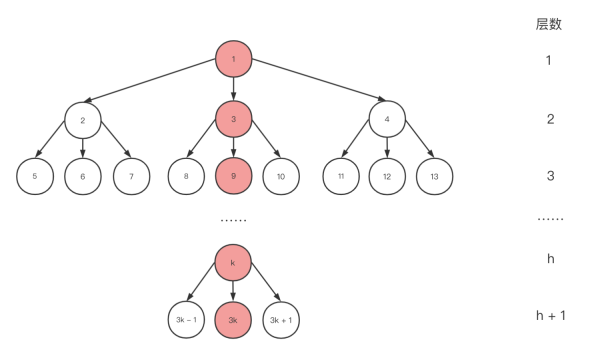
與二叉堆不同的是對于含有 N 個元素的 d 叉堆(通常情況下 d >= 2)，隨著 d 的增加，樹高 K = logdN 的斜率會下降，然而 d  越大，刪除操作的成本會更高。所以子元素不是越多越好，通常情況下三叉堆和四叉堆的應用會比較常見。

在libev中有這么一段注釋  https://github.com/enki/libev/blob/master/ev.c#L2227，他提及了四叉樹相比二叉堆來說緩存更加友好。  根據benchmark，在 50000+ 個 watchers 的場景下，四叉樹會有 5% 的性能優勢。

/*  * at the moment we allow libev the luxury of two heaps,  * a small-code-size 2-heap one and a ~1.5kb larger 4-heap  * which is more cache-efficient.  * the difference is about 5% with 50000+ watchers.  */

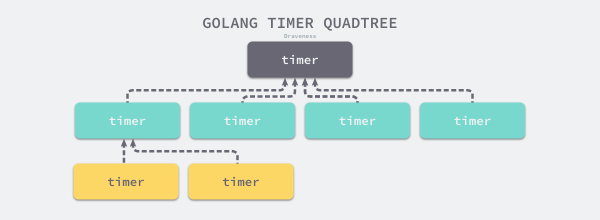
同樣 Go 語言中的定時器的 timersBucket 的數據結構也采用了最小四叉堆。

感謝各位的閱讀，以上就是“結合React源碼如何快速掌握優先隊列”的內容了，經過本文的學習后，相信大家對結合React源碼如何快速掌握優先隊列這一問題有了更深刻的體會，具體使用情況還需要大家實踐驗證。這里是億速云，小編將為大家推送更多相關知識點的文章，歡迎關注！