您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇文章為大家展示了利用python如何實現一個解析protobuf文件功能,內容簡明扼要并且容易理解,絕對能使你眼前一亮,通過這篇文章的詳細介紹希望你能有所收獲。
ply使用
簡介
如果你不是從事編譯器或者解析器的開發工作,你可能從未聽說過ply。ply是基于python的lex和yacc,而它的作者就是大名鼎鼎Python Cookbook, 3rd Edition的作者。可能有些朋友就納悶了,我一個業務開發怎么需要自己寫編譯器呢,各位編程大牛說過,中央決定了,要多嘗試新的東西。而且了解一些語法解析的姿勢,以后自己解析格式復雜的日志或者數學公式,也是非常有幫助的。
針對沒有編譯基礎的童鞋,強烈建議了解一些文法相關的基本概念。輪子哥強烈推薦的parsing techniques以及編譯龍虎鯨書,個人感覺都不適合入門學習,在此推薦胡倫俊的編譯原理(電子工業出版社),針對概念的例子講解很多,很適合入門學習。當然也不需要特別深入研究,知道詞法分析和語法分析的相關概念和方法就可以愉快的使用ply了。文檔鏈接: http://www.pchou.info/open-source/2014/01/18/52da47204d4cb.html
為了方便大家上手,以求解多元一次方程組為例,講解一下ply的使用。
例子說明
輸入是多個格式為x + 4y - 3.2z = 7的一次方程,為了讓例子盡可能簡單,做如下限制:
學過線性代數的童鞋肯定知道,只需要將方程組抽象為矩陣,按照線性代數的方法就可以解決。因此只需要將輸入方程組解析成右邊的矩陣和變量列表即可,剩下的求解過程就可以交給線性代數相關的工具解決。
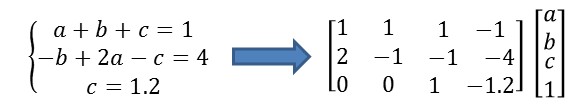
詞法解析
ply中的lex來做詞法解析,詞法解析的理論有一大堆,但是lex用起來卻非常直觀,就是用正則表達式的方式將文本字符串解析為一個一個的token,下面的代碼就是用lex實現詞法解析。
from ply import lex
# 空格 制表符 回車這些不可見符號都忽略
t_ignore = ' \t\r'
# 解析錯誤的時候直接拋出異常
def t_error(t):
raise Exception('error {} at line {}'.format(t.value[0], t.lineno))
# 記錄行號,方便出錯定位
def t_newline(t):
r'\n+'
t.lexer.lineno += len(t.value)
# 支持c++風格的\\注釋
def t_ignore_COMMENT(t):
r'\/\/[^\n]*'
# 變量的命令規則
def t_VARIABLE(t):
r'[a-z]+'
return t
# 常數命令規則
def t_CONSTANT(t):
r'\d+(\.\d+)?'
t.value = float(t.value)
return t
# 輸入中支持的符號頭token,當然也支持t_PLUS = r'\+'的方式將加號定義為token
literals = '+-,;='
tokens = ('VARIABLE', 'CONSTANT')
if __name__ == '__main__':
data = '''
-x + 2.4y + z = 0; //this is a comment
9y - z + 7.2x = -1;
y - z + x = 8
'''
lexer = lex.lex()
lexer.input(data)
while True:
tok = lexer.token()
if not tok:
break
print tok直接運行文件就可以將解析的token串打印出來,如下所示,詳細的使用文檔可以參考ply文檔。
LexToken(-,'-',2,5)
LexToken(VARIABLE,'x',2,6)
LexToken(+,'+',2,8)
LexToken(CONSTANT,2.4,2,10)
LexToken(VARIABLE,'y',2,13)
LexToken(+,'+',2,15)
LexToken(VARIABLE,'z',2,17)
LexToken(=,'=',2,19)
LexToken(CONSTANT,0.0,2,21)
LexToken(;,';',2,22)```
### 語法解析
ply中的yacc用作語法分析,雖然復雜的詞法分析可以代替簡單的語法分析,但類似于編程語言的解析再復雜的詞法分析也勝任不了。在使用yacc之前,需要了解上下文無關文法,這部分內容太多太雜,我也只了解部分簡單的概念,有興趣的可以看一看編譯原理深入了解。
目前語法分析的方法有兩大類,即自下向上的分析方法和自上而下的分析方法。所謂自上而下的分下法就是從文法的開始符號出發,根據文法規則正向推到出給定句子的一種方法,或者說,從樹根開始,往下構造語法樹,直到建立每個樹葉的分析方法。代表算法是LL(1),此算法文法解析能力不強,對文法定義要求比較高,主流的編譯器都沒有使用。自下而上的分析法是從給定的輸入串開始,根據文法規則逐步進行歸約,直至歸約到文法的開始符號,或者說從語法書的末端開始,步步向上歸約,直至歸約到根節點的分析方法。代表算法有SLR、LRLR,ply使用的就是LRLR。
因此我們只需要定義文法和規約動作即可,以下就是完整的代碼。
```python
# -*- coding=utf8 -*-
from ply import (
lex,
yacc
)
# 空格 制表符 回車這些不可見符號都忽略
t_ignore = ' \t\r'
# 解析錯誤的時候直接拋出異常
def t_error(t):
raise Exception('error {} at line {}'.format(t.value[0], t.lineno))
# 記錄行號,方便出錯定位
def t_newline(t):
r'\n+'
t.lexer.lineno += len(t.value)
# 支持c++風格的\\注釋
def t_ignore_COMMENT(t):
r'\/\/[^\n]*'
# 變量的命令規則
def t_VARIABLE(t):
r'[a-z]+'
return t
# 常數命令規則
def t_CONSTANT(t):
r'\d+(\.\d+)?'
t.value = float(t.value)
return t
# 輸入中支持的符號頭token,當然也支持t_PLUS = r'\+'的方式將加號定義為token
literals = '+-,;='
tokens = ('VARIABLE', 'CONSTANT')
# 頂層文法,規約的時候equations對應的p[1]是一個列表,包含了方程左邊各個變量與系數還有方程左邊的常數
def p_start(p):
"""start : equations"""
var_count, var_list = 0, []
for left, _ in p[1]:
for con, var_name in left:
if var_name in var_list:
continue
var_list.append(var_name)
var_count += 1
matrix = [[0] * (var_count + 1) for _ in xrange(len(p[1]))]
for counter, eq in enumerate(p[1]):
left, right = eq
for con, var_name in left:
matrix[counter][var_list.index(var_name)] = con
matrix[counter][-1] = -right
var_list.append(1)
p[0] = matrix, var_list
# 方程組對應的文法,每個方程用,或者;做分隔
def p_equations(p):
"""equations : equation ',' equations
| equation ';' equations
| equation"""
if len(p) == 2:
p[0] = [p[1]]
else:
p[0] = [p[1]] + p[3]
# 單個方程對應的文法
def p_equation(p):
"""equation : eq_left '=' eq_right"""
p[0] = (p[1], p[3])
# 方程等式左邊對應的文法
def p_eq_left(p):
"""eq_left : var_unit eq_left
|"""
if len(p) == 1:
p[0] = []
else:
p[0] = [p[1]] + p[2]
# 六種文法對應例子: x, 5x, +x, -x, +4x, -4y
# 歸約的形式是一個元組,例: (5, 'x')
def p_var_unit(p):
"""var_unit : VARIABLE
| CONSTANT VARIABLE
| '+' VARIABLE
| '-' VARIABLE
| '+' CONSTANT VARIABLE
| '-' CONSTANT VARIABLE"""
len_p = len(p)
if len_p == 2:
p[0] = (1.0, p[1])
elif len_p == 3:
if p[1] == '+':
p[0] = (1.0, p[2])
elif p[1] == '-':
p[0] = (-1.0, p[2])
else:
p[0] = (p[1], p[2])
else:
if p[1] == '+':
p[0] = (p[2], p[3])
else:
p[0] = (-p[2], p[3])
# 方程等式右邊對應的常數,對應的例子:1.2, +1.2, -1.2
def p_eq_right(p):
"""eq_right : CONSTANT
| '+' CONSTANT
| '-' CONSTANT"""
if len(p) == 3:
if p[1] == '-':
p[0] = -p[2]
else:
p[0] = p[2]
else:
p[0] = p[1]
if __name__ == '__main__':
data = '''
-x + 2.4y + z = 0; //this is a comment
9y - z + 7.2x = -1;
y - z + x = 8
'''
lexer = lex.lex()
parser = yacc.yacc(debug=True)
lexer.lineno = 1
s = parser.parse(data)
print s直接運行文件即可,得到的輸出如下,之后就可以根據線性代數的方法求解各個變量的值
([[-1.0, 2.4, 1.0, -0.0], [7.2, 9.0, -1.0, 1.0], [1.0, 1.0, -1.0, -8.0]], ['x', 'y', 'z', 1])
上述內容就是利用python如何實現一個解析protobuf文件功能,你們學到知識或技能了嗎?如果還想學到更多技能或者豐富自己的知識儲備,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。