java實現最短路徑算法之Dijkstra算法的示例

這篇文章主要介紹了java實現最短路徑算法之Dijkstra算法的示例，具有一定借鑒價值，感興趣的朋友可以參考下，希望大家閱讀完這篇文章之后大有收獲，下面讓小編帶著大家一起了解一下。

一、知識準備：

1、表示圖的數據結構

用于存儲圖的數據結構有多種，本算法中筆者使用的是鄰接矩陣。

圖的鄰接矩陣存儲方式是用兩個數組來表示圖。一個一維數組存儲圖中頂點信息，一個二維數組（鄰接矩陣）存儲圖中的邊或弧的信息。

設圖G有n個頂點，則鄰接矩陣是一個n*n的方陣，定義為：

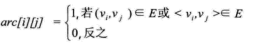
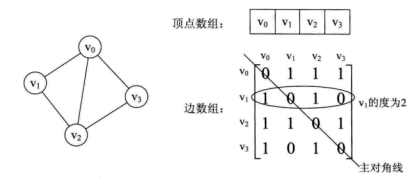
從上面可以看出，無向圖的邊數組是一個對稱矩陣。所謂對稱矩陣就是n階矩陣的元滿足aij = aji。即從矩陣的左上角到右下角的主對角線為軸，右上角的元和左下角相對應的元全都是相等的。

從這個矩陣中，很容易知道圖中的信息。

（1）要判斷任意兩頂點是否有邊無邊就很容易了；

（2）要知道某個頂點的度，其實就是這個頂點vi在鄰接矩陣中第i行或（第i列）的元素之和；

（3）求頂點vi的所有鄰接點就是將矩陣中第i行元素掃描一遍，arc[i][j]為1就是鄰接點；

而有向圖講究入度和出度，頂點vi的入度為1，正好是第i列各數之和。頂點vi的出度為2，即第i行的各數之和。

有向圖的定義也類似，故不做贅述。

2、單起點全路徑

所謂單起點全路徑，就是指在一個圖中，從一個起點出發，到所有節點的最短路徑。 

3、圖論的基本知識(讀者需自行尋找相關資料)

4、互補松弛條件

設標量d1,d2,....,dN滿足

dj<=di + aij,  (i,j)屬于A,

且P是以i1為起點ik為終點的路，如果

dj = di + aij, 對P的所有邊(i, j)

成立，那么P是從i1到ik的最短路。其中，滿足上面兩式的被稱為最短路問題的互補松弛條件。

二、算法思想

1、令G = （V，E）為一個帶權無向圖。G中若有兩個相鄰的節點,i和j。aij(在這及其后面都表示為下標，請注意)為節點i到節點j的權值，在本算法可以理解為距離。每個節點都有一個值di(節點標記)表示其從起點到它的某條路的距離。

2、算法初始有一個數組V用于儲存未訪問節點的列表，我們暫稱為候選列表。選定節點1為起始節點。開始時，節點1的d1=0, 其他節點di=無窮大，V為所有節點。
初始化條件后，然后開始迭代算法，直到V為空集時停止。具體迭代步驟如下：

將d值最小的節點di從候選列表中移除。(本例中V的數據結構采用的是優先隊列實現最小值出列，最好使用斐波那契對，在以前文章有過介紹，性能有大幅提示)。對于以該節點為起點的每一條邊，不包括移除V的節點, (i, j)屬于A， 若dj > di + aij（違反松弛條件）,則令

dj = di + aij    , （如果j已經從V中移除過，說明其最小距離已經計算出，不參與此次計算）

可以看到在算法的運算工程中，節點的d值是單調不增的

具體算法圖解如下

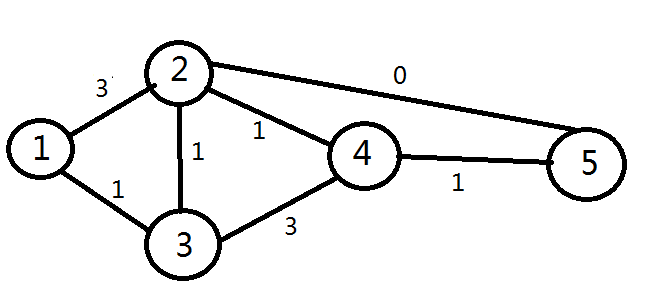
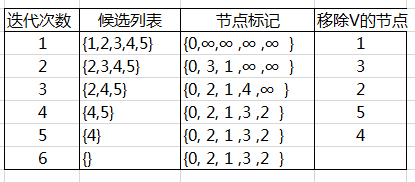
三、java代碼實現

public class Vertex implements Comparable<Vertex>{

  /**
   * 節點名稱(A,B,C,D)
   */
  private String name;
  
  /**
   * 最短路徑長度
   */
  private int path;
  
  /**
   * 節點是否已經出列(是否已經處理完畢)
   */
  private boolean isMarked;
  
  public Vertex(String name){
    this.name = name;
    this.path = Integer.MAX_VALUE; //初始設置為無窮大
    this.setMarked(false);
  }
  
  public Vertex(String name, int path){
    this.name = name;
    this.path = path;
    this.setMarked(false);
  }
  
  @Override
  public int compareTo(Vertex o) {
    return o.path > path?-1:1;
  }
}

public class Graph {

  /*
   * 頂點
   */
  private List<Vertex> vertexs;

  /*
   * 邊
   */
  private int[][] edges;

  /*
   * 沒有訪問的頂點
   */
  private Queue<Vertex> unVisited;

  public Graph(List<Vertex> vertexs, int[][] edges) {
    this.vertexs = vertexs;
    this.edges = edges;
    initUnVisited();
  }
  
  /*
   * 搜索各頂點最短路徑
   */
  public void search(){
    while(!unVisited.isEmpty()){
      Vertex vertex = unVisited.element();
      //頂點已經計算出最短路徑，設置為"已訪問"
     　　vertex.setMarked(true);  
      //獲取所有"未訪問"的鄰居
      　　List<Vertex> neighbors = getNeighbors(vertex);  
      //更新鄰居的最短路徑
      updatesDistance(vertex, neighbors);    
      pop();
    }
    System.out.println("search over");
  }
  
  /*
   * 更新所有鄰居的最短路徑
   */
  private void updatesDistance(Vertex vertex, List<Vertex> neighbors){
    for(Vertex neighbor: neighbors){
      updateDistance(vertex, neighbor);
    }
  }
  
  /*
   * 更新鄰居的最短路徑
   */
  private void updateDistance(Vertex vertex, Vertex neighbor){
    int distance = getDistance(vertex, neighbor) + vertex.getPath();
    if(distance < neighbor.getPath()){
      neighbor.setPath(distance);
    }
  }

  /*
   * 初始化未訪問頂點集合
   */
  private void initUnVisited() {
    unVisited = new PriorityQueue<Vertex>();
    for (Vertex v : vertexs) {
      unVisited.add(v);
    }
  }

  /*
   * 從未訪問頂點集合中刪除已找到最短路徑的節點
   */
  private void pop() {
    unVisited.poll();
  }

  /*
   * 獲取頂點到目標頂點的距離
   */
  private int getDistance(Vertex source, Vertex destination) {
    int sourceIndex = vertexs.indexOf(source);
    int destIndex = vertexs.indexOf(destination);
    return edges[sourceIndex][destIndex];
  }

  /*
   * 獲取頂點所有(未訪問的)鄰居
   */
  private List<Vertex> getNeighbors(Vertex v) {
    List<Vertex> neighbors = new ArrayList<Vertex>();
    int position = vertexs.indexOf(v);
    Vertex neighbor = null;
    int distance;
    for (int i = 0; i < vertexs.size(); i++) {
      if (i == position) {
        //頂點本身，跳過
        continue;
      }
      distance = edges[position][i];  //到所有頂點的距離
      if (distance < Integer.MAX_VALUE) {
        //是鄰居(有路徑可達)
        neighbor = getVertex(i);
        if (!neighbor.isMarked()) {
          //如果鄰居沒有訪問過，則加入list;
          neighbors.add(neighbor);
        }
      }
    }
    return neighbors;
  }

  /*
   * 根據頂點位置獲取頂點
   */
  private Vertex getVertex(int index) {
    return vertexs.get(index);
  }

  /*
   * 打印圖
   */
  public void printGraph() {
    int verNums = vertexs.size();
    for (int row = 0; row < verNums; row++) {
      for (int col = 0; col < verNums; col++) {
        if(Integer.MAX_VALUE == edges[row][col]){
          System.out.print("X");
          System.out.print(" ");
          continue;
        }
        System.out.print(edges[row][col]);
        System.out.print(" ");
      }
      System.out.println();
    }
  }
}

public class Test {

  public static void main(String[] args){
    List<Vertex> vertexs = new ArrayList<Vertex>();
    Vertex a = new Vertex("A", 0);
    Vertex b = new Vertex("B");
    Vertex c = new Vertex("C");
    Vertex d = new Vertex("D");
    Vertex e = new Vertex("E");
    Vertex f = new Vertex("F");
    vertexs.add(a);
    vertexs.add(b);
    vertexs.add(c);
    vertexs.add(d);
    vertexs.add(e);
    vertexs.add(f);
    int[][] edges = {
        {Integer.MAX_VALUE,6,3,Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {6,Integer.MAX_VALUE,2,5,Integer.MAX_VALUE,Integer.MAX_VALUE},
        {3,2,Integer.MAX_VALUE,3,4,Integer.MAX_VALUE},
        {Integer.MAX_VALUE,5,3,Integer.MAX_VALUE,5,3},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,4,5,Integer.MAX_VALUE,5},
        {Integer.MAX_VALUE,Integer.MAX_VALUE,Integer.MAX_VALUE,3,5,Integer.MAX_VALUE}
    
    };
    Graph graph = new Graph(vertexs, edges);
    graph.printGraph();
    graph.search();
  }
  
}

感謝你能夠認真閱讀完這篇文章，希望小編分享的“java實現最短路徑算法之Dijkstra算法的示例”這篇文章對大家有幫助，同時也希望大家多多支持億速云，關注億速云行業資訊頻道，更多相關知識等著你來學習!