java中怎么計算圖兩點之間的所有路徑

java中怎么計算圖兩點之間的所有路徑？針對這個問題，這篇文章詳細介紹了相對應的分析和解答，希望可以幫助更多想解決這個問題的小伙伴找到更簡單易行的方法。

1.給定圖如下:

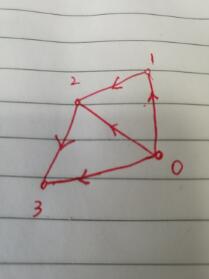
2.求0到3之間可達的所有路徑

這里問題就是關于搜索遍歷的問題,但其中需要注意到不能產生回路或環.

算法描述如下:

top_node:當前棧頂元素

adjvex_node;當前top_node已經訪問的鄰接點

next_node:即將訪問的元素（top_node的第adjvex_node個鄰接點所對應的元素）

找出所有路徑采用的是遍歷的方法，以“深度優先”算法為基礎。從源點出發，先到源點的第一個鄰接點N00，再到N00的第一個鄰接點N10，再到N10的第一個鄰接點N20...當遍歷到目標點時表明找到一條路徑。

上述代碼的核心數據結構為一個棧，主要步驟：

①源點先入棧，并進行標記

②獲取棧頂元素top_node，如果棧頂為終點時，即找到一條路徑,棧頂元素top_node出棧，此時adjvex_node=top_node,新的棧頂元素為top_node，否則執行③

③從top_node的所有鄰接點中，從adjvex_node為起點，選取下一個鄰接點next_node；如果該元素非空,則入棧,使得adjvex_node=-1,(adjvex_node=-1代表top_node的鄰接點一個還沒有訪問)做入棧標記。否則代表沒有后續節點了,此時必須出棧棧頂元素,并置adjvex_node為該棧頂元素,并做出棧標記。

④為避免回路，已入棧元素要記錄，選取新入棧頂點時應跳過已入棧的頂點,當棧為空時，遍歷完成

3.java代碼實現

1)圖結構

點表

public class Vertex {
//存放點信息
public int data;
//與該點鄰接的第一個邊節點
public Edge firstEdge;
}

邊表(代表與點相連的點的集合)

//邊節點
public class Edge {
//對應的點下表
public int vertexId;
//邊的權重
public int weight;
//下一個邊節點
public Edge next;
//getter and setter自行補充
}

2).算法實現

import java.util.HashMap;
import java.util.Map;
import java.util.Stack;
public class graph {
public Vertex[] vertexList; //存放點的集合
public graph(int vertexNum){
 this.vertexNum=vertexNum;
 vertexList=new Vertex[vertexNum];
}
//點個數
public int vertexNum;
//邊個數
public int edgeLength;
public void initVertext(int datas[]){
 for(int i=0;i<vertexNum;i++){
 Vertex vertext=new Vertex();
 vertext.data=datas[i];
 vertext.firstEdge=null;
 vertexList[i]=vertext;
 //System.out.println("i"+vertexList[i]);
 }
 isVisited=new boolean[vertexNum];
 for(int i=0;i<isVisited.length;i++){
 isVisited[i]=false;
 }
}
//針對x節點添加邊節點y
public void addEdge(int x,int y,int weight){
 Edge edge=new Edge();
 edge.setVertexId(y);
 edge.setWeight(weight);
 //第一個邊節點
 System.out.println(vertexList.length);
 if(null==vertexList[x].firstEdge){
 vertexList[x].firstEdge=edge;
 edge.setNext(null);
 }
 //不是第一個邊節點,則采用頭插法
 else{
 edge.next=vertexList[x].firstEdge;
 vertexList[x].firstEdge=edge;
 }
}
//得到x的鄰接點為y的后一個鄰接點位置,為-1說明沒有找到
public int getNextNode(int x,int y){
 int next_node=-1;
 Edge edge=vertexList[x].firstEdge;
 if(null!=edge&&y==-1){
 int n=edge.vertexId;
 //元素還不在stack中
 if(!states.get(n))
  return n;
 return -1;
 }
 
 while(null!=edge){
 //節點未訪問
 if(edge.vertexId==y){
  if(null!=edge.next){
   next_node=edge.next.vertexId;
  if(!states.get(next_node))
  return next_node;
  }
  else
  return -1;
 }
 edge=edge.next;
 }
 return -1;
}
//代表某節點是否在stack中,避免產生回路
public Map<Integer,Boolean> states=new HashMap();
 
//存放放入stack中的節點
public Stack<Integer> stack=new Stack();
 
//輸出2個節點之間的輸出路徑
public void visit(int x,int y){
    //初始化所有節點在stack中的情況
    for(int i=0;i<vertexNum;i++){
 states.put(i,false);
 }
    //stack top元素
    int top_node;
 //存放當前top元素已經訪問過的鄰接點,若不存在則置-1,此時代表訪問該top元素的第一個鄰接點
    int adjvex_node=-1;
 int next_node;
 stack.add(x);
 states.put(x,true);
 while(!stack.isEmpty()){
 top_node=stack.peek();
 //找到需要訪問的節點
        if(top_node==y){
  //打印該路徑
  printPath();
  adjvex_node=stack.pop();
  states.put(adjvex_node,false);
 }
 else{
  //訪問top_node的第advex_node個鄰接點
            next_node=getNextNode(top_node,adjvex_node);
  if(next_node!=-1){
  stack.push(next_node);
  //置當前節點訪問狀態為已在stack中
                states.put(next_node,true);
  //臨接點重置
                adjvex_node=-1;
  }
            //不存在臨接點，將stack top元素退出 
            else{
  //當前已經訪問過了top_node的第adjvex_node鄰接點
                adjvex_node=stack.pop();
  //不在stack中
  states.put(adjvex_node,false);
  }
 }
 }
}
 
//打印stack中信息,即路徑信息
 public void printPath(){
 StringBuilder sb=new StringBuilder();
 for(Integer i :stack){
 sb.append(i+"->");
 }
 sb.delete(sb.length()-2,sb.length());
 System.out.println(sb.toString());
}
 
public static void main(String[]args){
 graph g=new graph(5);
 g.initVertext(new int[]{1,2,3,4,4});
 //System.out.println(g.vertexList[0]);
 g.addEdge(0,1,1);
 g.addEdge(0,2,3);
 g.addEdge(0,3,4);
 g.addEdge(1,2,1);
 g.addEdge(2,0,1);
 g.addEdge(2,3,1);
 g.addEdge(1,3,2);
 g.visit(0,3);
}
}

執行結果如下:

0->3
0->2->3
0->1->2->3 

關于java中怎么計算圖兩點之間的所有路徑問題的解答就分享到這里了，希望以上內容可以對大家有一定的幫助，如果你還有很多疑惑沒有解開，可以關注億速云行業資訊頻道了解更多相關知識。