基于Numpy.convolve使用Python實現滑動平均濾波的思路詳解

​

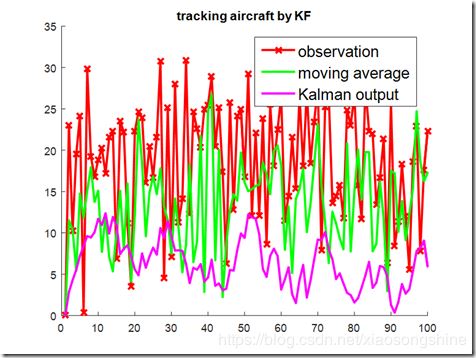
1.滑動平均概念

滑動平均濾波法（又稱遞推平均濾波法），時把連續取N個采樣值看成一個隊列 ，隊列的長度固定為N ，每次采樣到一個新數據放入隊尾,并扔掉原來隊首的一次數據.(先進先出原則)  把隊列中的N個數據進行算術平均運算,就可獲得新的濾波結果。N值的選取：流量，N=12；壓力：N=4；液面，N=4~12；溫度，N=1~4

優點：  對周期性干擾有良好的抑制作用，平滑度高  適用于高頻振蕩的系統 

缺點：  靈敏度低  對偶然出現的脈沖性干擾的抑制作用較差  不易消除由于脈沖干擾所引起的采樣值偏差  不適用于脈沖干擾比較嚴重的場合  比較浪費RAM 

2.解決思路

可以發現滑動平均濾波法計算很類似與一維卷積的工作原理，滑動平均的N就對應一維卷積核大小（長度）。

步長會有些區別，滑動平均濾波法滑動步長為1，而一維卷積步長可以自定義。還有區別就是一維卷積的核參數是需要更新迭代的，而滑動平均濾波法核參數都是一。

我們應該怎么利用這個相似性呢？其實也很簡單，只需要把一維卷積核大小（長度）和N相等，步長設置為1，核參數都初始為1就可以了。由于一維卷積具備速度快，然后我們就可以使用一維卷積來實現這個功能了，快速高效。

使用深度學習框架實現這個功能是否有些大材小用了？是有些大材小用了，因為這里使用卷積的核參數不用更新，其實沒必要使用復雜的深度學習框架，如果Numpy中可以實現這些功能就更簡單方便了。

說干就干，經過查找發現Numpy.convolve可以實現我們想要的功能。

3.Numpy.convolve介紹

numpy.convolve(a, v, mode=‘full')

參數：
　　　　a:(N,)輸入的一維數組
　　　　v:(M,)輸入的第二個一維數組
　　　　mode:{‘full', ‘valid', ‘same'}參數可選
　　　　　　‘full'　默認值，返回每一個卷積值，長度是N+M-1,在卷積的邊緣處，信號不重疊，存在邊際效應。
　　　　　　‘same'　返回的數組長度為max(M, N),邊際效應依舊存在。
　　　　　　‘valid' 　返回的數組長度為max(M,N)-min(M,N)+1,此時返回的是完全重疊的點。邊緣的點無效。

和一維卷積參數類似，a就是被卷積數據，v是卷積核大小。

4.算法實現

def np_move_avg(a,n,mode="same"):
  return(np.convolve(a, np.ones((n,))/n, mode=mode))

原理說明

運行平均值是卷積數學運算的一個例子。對于運行平均值，沿著輸入滑動窗口并計算窗口內容的平均值。對于離散的1D信號，卷積是相同的，除了代替計算任意線性組合的平均值，即將每個元素乘以相應的系數并將結果相加。那些系數，一個用于窗口中的每個位置，有時稱為卷積核。現在，N值的算術平均值是(x_1 + x_2 + ... + x_N) / N，所以相應的內核是(1/N, 1/N, ..., 1/N)，這正是我們通過使用得到的np.ones((N,))/N。

邊緣處理

該mode的參數np.convolve指定如何處理邊緣。在這里選擇了same模式，這樣可以保證輸出長度一種，但你可能還有其他優先事項。這是一個說明模式之間差異的圖：

import numpy as np
import matplotlib.pyplot as plt
def np_move_avg(a,n,mode="same"):
  return(np.convolve(a, np.ones((n,))/n, mode=mode))
modes = ['full', 'same', 'valid']
for m in modes:
  plt.plot(np_move_avg(np.ones((200,)), 50, mode=m));
plt.axis([-10, 251, -.1, 1.1]);
plt.legend(modes, loc='lower center');
plt.show() ​

​

5.參考

1. https://stackoverflow.com/questions/13728392/moving-average-or-running-mean

總結

以上所述是小編給大家介紹的Python實現滑動平均濾波的思路詳解（基于Numpy.convolve），希望對大家有所幫助，如果大家有任何疑問歡迎給我留言，小編會及時回復大家的！