您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本次選取泰坦尼克號的數據,利用python進行抽樣分布描述及實踐。
備注:數據集的原始數據是泰坦尼克號的數據,本次截取了其中的一部分數據進行學習。Age:年齡,指登船者的年齡。Fare:價格,指船票價格。Embark:登船的港口。
1、按照港口分類,使用python求出各類港口數據 年齡、車票價格的統計量(均值、方差、標準差、變異系數等)。
import pandas as pd
df = pd.read_excel('/Users/Downloads/data.xlsx',usecols = [1,2,3] )
#拿到港口'Embarked'、年齡'Age'、價格'Fare'的數據
df2 = df.groupby(['Embarked'])
#按照港口'Embarked'分類后,查看 年齡、車票價格的統計量。
# 變異系數 = 標準差/平均值
def cv(data):
return data.std()/data.var()
df2 = df.groupby(['Embarked']).agg(['count','min','max','median','mean','var','std',cv])
df2 = df2.apply(lambda x:round(x,2))
df2_age = df2['Age']
df2_fare = df2['Fare']
分類后 年齡及價格統計量描述數據如下圖:
年齡統計量

價格統計量

2、畫出價格的分布圖像,驗證數據服從何種分布(正態?卡方?還是T?)
2.1 畫出船票的直方圖:
plt.hist(df['Fare'],20,normed=1, alpha=0.75)
plt.title('Fare')
plt.grid(True)
船票價格的直方圖及概率分布
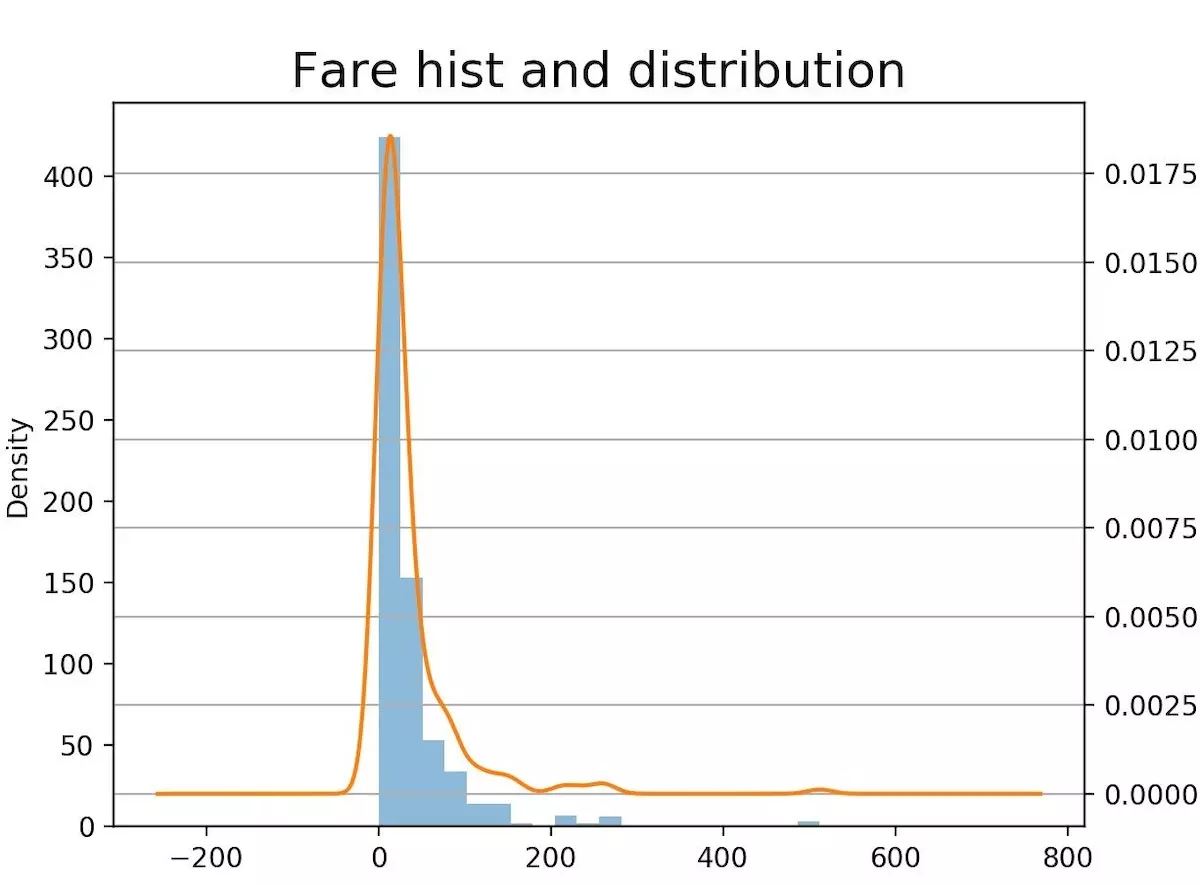
2.2 驗證是否符合正態分布?
#分別用kstest、shapiro、normaltest來驗證分布系數 ks_test = kstest(df['Fare'], 'norm') #KstestResult(statistic=0.99013849978633, pvalue=0.0) shapiro_test = shapiro(df['Fare']) #shapiroResult(0.5256513357162476, 7.001769945799311e-40) normaltest_test = normaltest(df['Fare'],axis=0) #NormaltestResult(statistic=715.0752414548335, pvalue=5.289130045259168e-156)
以上三種檢測結果表明 p<5%,因此 船票數據不符合正態分布。
繪制擬合正態分布曲線:
fare = df['Fare']
plt.figure()
fare.plot(kind = 'kde') #原始數據的正態分布
M_S = stats.norm.fit(fare) #正態分布擬合的平均值loc,標準差 scale
normalDistribution = stats.norm(M_S[0], M_S[1]) # 繪制擬合的正態分布圖
x = np.linspace(normalDistribution.ppf(0.01), normalDistribution.ppf(0.99), 100)
plt.plot(x, normalDistribution.pdf(x), c='orange')
plt.xlabel('Fare about Titanic')
plt.title('Titanic[Fare] on NormalDistribution', size=20)
plt.legend(['Origin', 'NormDistribution'])
船票擬合正態分布曲線
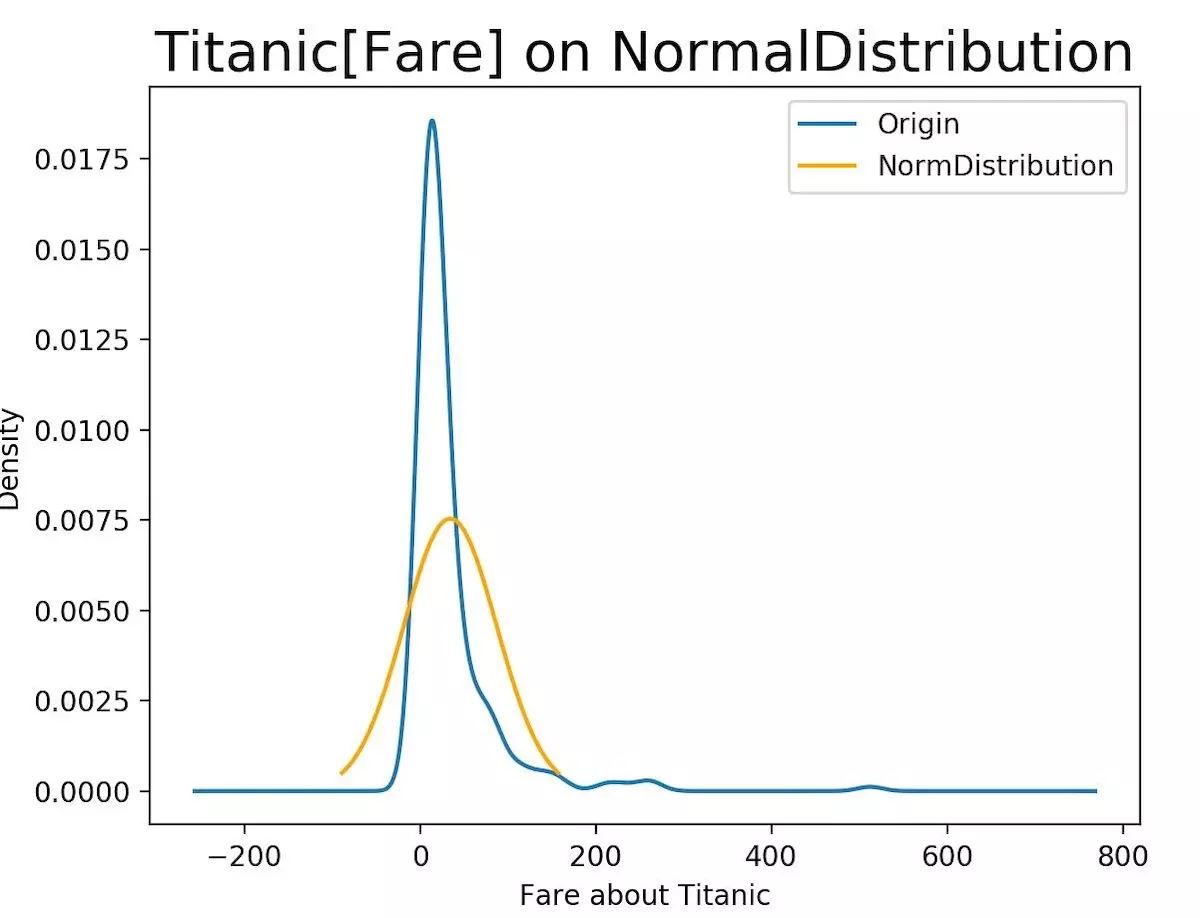
2.3 驗證是否符合T分布?
T_S = stats.t.fit(fare) df = T_S[0] loc = T_S[1] scale = T_S[2] x2 = stats.t.rvs(df=df, loc=loc, scale=scale, size=len(fare)) D, p = stats.ks_2samp(fare, x2) # (0.25842696629213485 2.6844476044528504e-21)
p = 2.6844476044528504e-21 ,p < alpha,拒絕原假設,價格數據不符合t分布。
對票價數據進行T分布擬合:
plt.figure()
fare.plot(kind = 'kde')
TDistribution = stats.t(T_S[0], T_S[1],T_S[2]) # 繪制擬合的T分布圖
x = np.linspace(TDistribution.ppf(0.01), TDistribution.ppf(0.99), 100)
plt.plot(x, TDistribution.pdf(x), c='orange')
plt.xlabel('Fare about Titanic')
plt.title('Titanic[Fare] on TDistribution', size=20)
plt.legend(['Origin', 'TDistribution'])
票價擬合T分布

2.4 驗證是否符合卡方分布?
chi_S = stats.chi2.fit(fare) df_chi = chi_S[0] loc_chi = chi_S[1] scale_chi = chi_S[2] x2 = stats.chi2.rvs(df=df_chi, loc=loc_chi, scale=scale_chi, size=len(fare)) Df, pf = stats.ks_2samp(fare, x2) # (0.16292134831460675, 1.154755913291936e-08)
p = 1.154755913291936e-08 ,p < alpha,拒絕原假設,價格數據不符合卡方分布。
對票價數據進行卡方分布擬合
plt.figure()
fare.plot(kind = 'kde')
chiDistribution = stats.chi2(chi_S[0], chi_S[1],chi_S[2]) # 繪制擬合的正態分布圖
x = np.linspace(chiDistribution.ppf(0.01), chiDistribution.ppf(0.99), 100)
plt.plot(x, chiDistribution.pdf(x), c='orange')
plt.xlabel('Fare about Titanic')
plt.title('Titanic[Fare] on chi-square_Distribution', size=20)
plt.legend(['Origin', 'chi-square_Distribution'])
票價擬合卡方分布
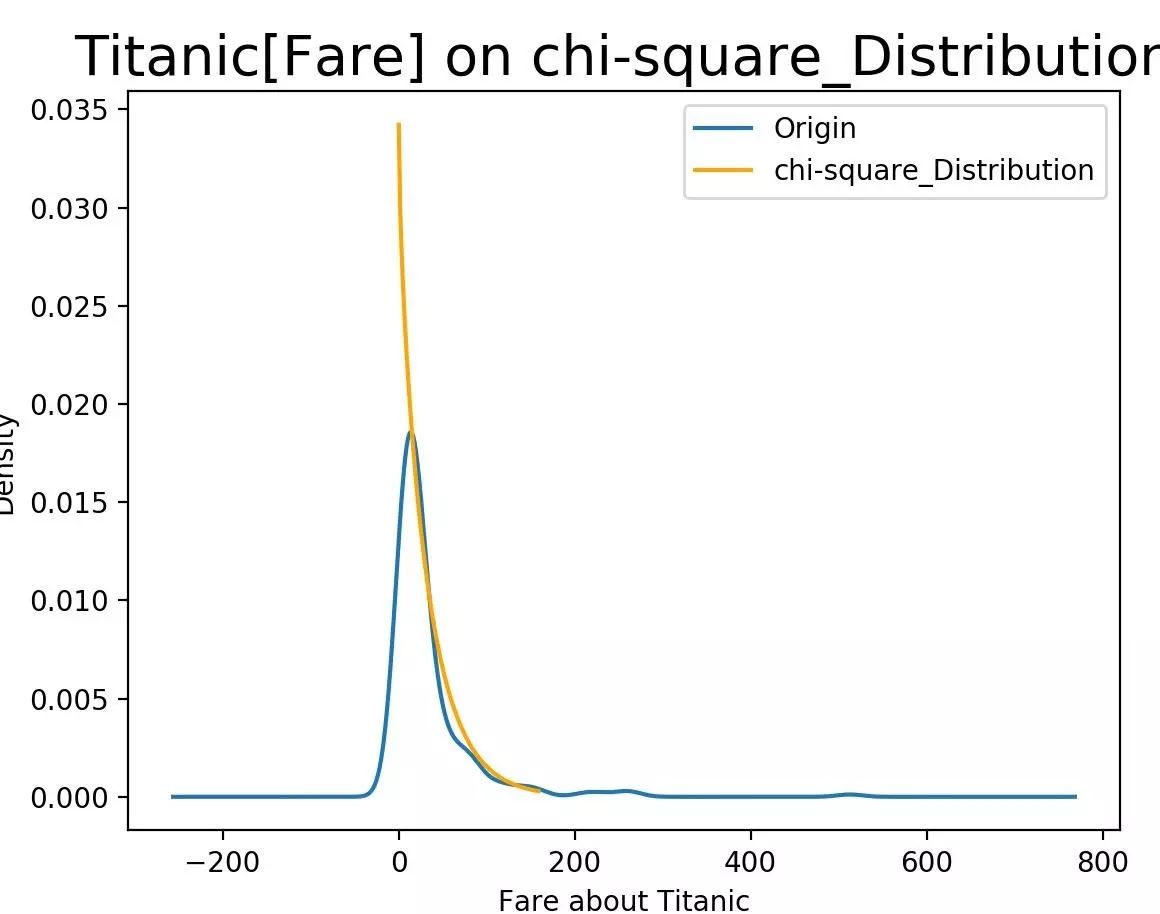
3、按照港口分類,驗證S與Q兩個港口間的價格之差是否服從某種分布
S_fare = df[df['Embarked'] =='S']['Fare'] Q_fare = df[df['Embarked'] =='Q']['Fare'] C_fare = df[df['Embarked'] =='C']['Fare'] S_fare.describe() count 554.000000 mean 27.476284 std 36.546362 min 0.000000 25% 8.050000 50% 13.000000 75% 27.862500 max 263.000000 Q_fare.describe() count 28.000000 mean 18.265775 std 21.843582 min 6.750000 25% 7.750000 50% 7.750000 75% 18.906250 max 90.000000 C_fare.describe() count 130.000000 mean 68.296767 std 90.557822 min 4.012500 25% 14.454200 50% 36.252100 75% 81.428100 max 512.329200
按照港口分類后,S港口樣本數<=554,Q港口樣本數<=28,C港口樣本數<=130。
總體不服從正態分布,所以需要當n比較大時,一般要求n>=30,兩個樣本均值之差的抽樣分布可近似為正態分布。X2的總體容量為28,其樣本容量不可能超過30,故其S港和Q港兩個樣本均值之差(E(X1)-E(X2))的抽樣分布不服從正態分布。
S港和C港兩個樣本均值之差(E(X1)-E(X3))的抽樣分布近似服從正態分布,其均值和方差分別為E(E(X1) - E(X3)) = E(E(X1)) - E(E(X3)) = μ1 - μ3;D(E(X1) + E(X3)) = D(E(X1)) + D(E(X3)) = σ1²/n1 + σ3²/n3 。繪圖如下:
miu = np.mean(S_fare) - np.mean(C_fare)
sig = np.sqrt(np.var(S_fare, ddof=1)/len(S_fare) + np.var(C_fare, ddof=1)/len(C_fare))
x = np.arange(- 110, 50)
y = stats.norm.pdf(x, miu, sig)
plt.plot(x, y)
plt.xlabel("S_Fare - C_Fare")
plt.ylabel("Density")
plt.title('Fare difference between S and C')
plt.show()
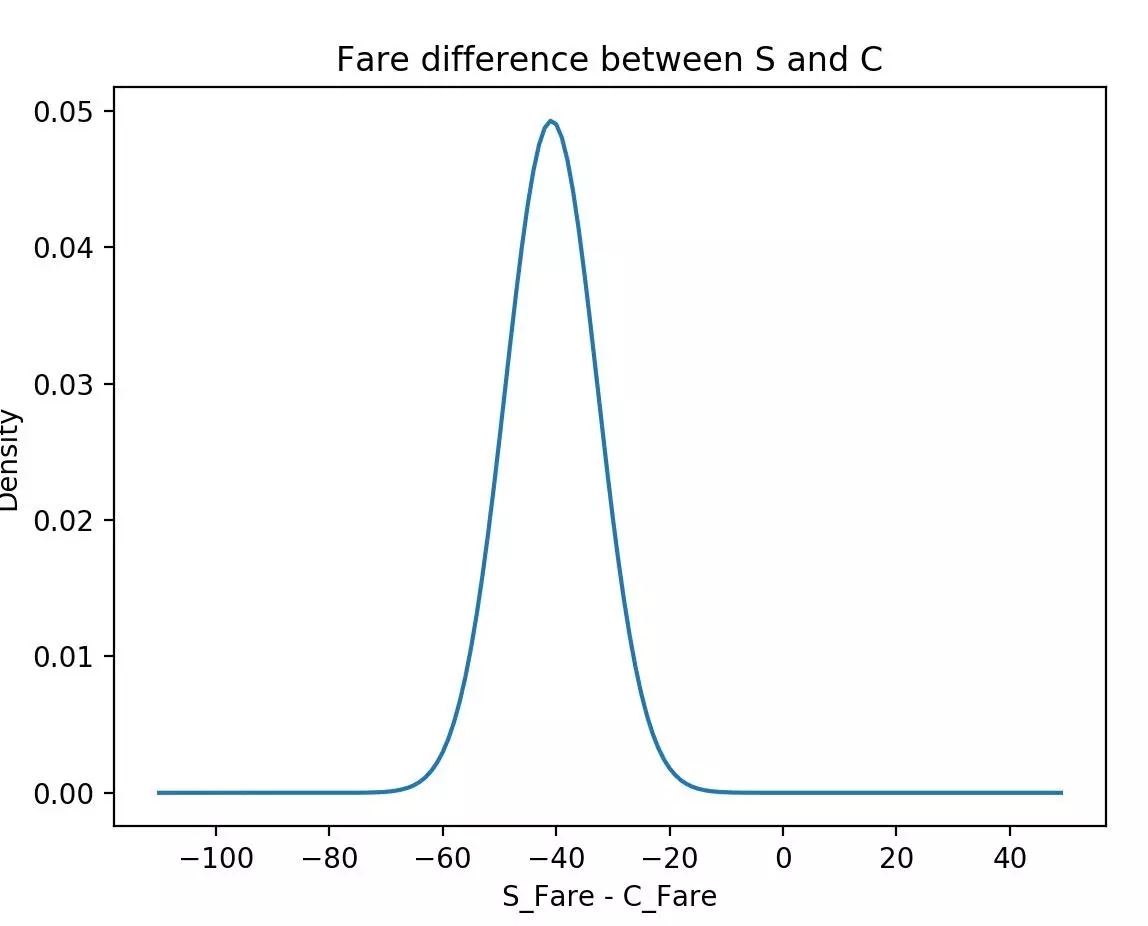
以上就是本文的全部內容,希望對大家的學習有所幫助,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。