您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
何為共線性:
共線性問題指的是輸入的自變量之間存在較高的線性相關度。共線性問題會導致回歸模型的穩定性和準確性大大降低,另外,過多無關的維度計算也很浪費時間
共線性產生原因:
變量出現共線性的原因:
數據樣本不夠,導致共線性存在偶然性,這其實反映了缺少數據對于數據建模的影響,共線性僅僅是影響的一部分
多個變量都給予時間有共同或相反的演變趨勢,例如春節期間的網絡銷售量和銷售額都相對與正常時間有下降趨勢。
多個變量存在一定的推移關系,但總體上變量間的趨勢一致,只是發生的時間點不一致,例如廣告費用和銷售額之間,通常是品牌廣告先進行大范圍的曝光和信息推送,經過一定時間傳播之后,才會在銷售額上做出反映。
多變量之間存在線性的關系。例如y代表訪客數,用x代表展示廣告費用,那么二者的關系很可能是y=2*x + b
如何檢驗共線性:
檢驗共線性:
容忍度(Tolerance):容忍度是每個自變量作為因變量對其他自變量進行回歸建模時得到的殘差比例,大小用1減得到的決定系數來表示。容忍度值越小說明這個自變量與其他自變量間越可能存在共線性問題。
方差膨脹因子 VIF是容忍度的倒數,值越大則共線性問題越明顯,通常以10作為判斷邊界。當VIF<10,不存在多重共線性;當10<=VIF<100,存在較強的多重共線性;當VIF>=100, 存在嚴重多重共線性。
特征值(Eigenvalue):該方法實際上就是對自變量做主成分分析,如果多個維度的特征值等于0,則可能有比較嚴重的共線性。
相關系數:如果相關系數R>0.8時就可能存在較強相關性
如何處理共線性:
處理共線性:
增大樣本量:增大樣本量可以消除猶豫數據量不足而出現的偶然的共線性現象,在可行的前提下這種方法是需要優先考慮的
嶺回歸法(Ridge Regression):實際上是一種改良最小二乘估計法。通過放棄最小二乘法的無偏性,以損失部分信息、降低精度為代價來獲得更實際和可靠性更強的回歸系數。因此嶺回歸在存在較強共線性的回歸應用中較為常用。
逐步回歸法(Stepwise Regression):每次引入一個自變量進行統計檢驗,然后逐步引入其他變量,同時對所有變量的回歸系數進行檢驗,如果原來引入的變量由于后面變量的引入而變得不再顯著,那么久將其剔除,逐步得到最有回歸方程。
主成分回歸(Principal Components Regression):通過主成分分析,將原始參與建模的變量轉換為少數幾個主成分,么個主成分是原變量的線性組合,然后基于主成分做回歸分析,這樣也可以在不丟失重要數據特征的前提下避開共線性問題。
人工去除:結合人工經驗,對自變量進行刪減,但是對操作者的業務能力、經驗有很高的要求。
部分方法python代碼實現
import numpy as np
import pandas as pd
from sklearn.linear_model import Ridge
from sklearn.decomposition import PCA
from sklearn.linear_model import LinearRegression
# 導入數據
df = pd.read_csv('https://raw.githubusercontent.com/ffzs/dataset/master/boston/train.csv')
# 切分自變量
X = df.iloc[:, 1:-1].values
# 切分預測變量
y = df.iloc[:, [-1]].values
# 使用嶺回歸處理
import matplotlib.pyplot as plt
plt.figure(figsize=(8,6))
n_alphas = 20
alphas = np.logspace(-1,4,num=n_alphas)
coefs = []
for a in alphas:
ridge = Ridge(alpha=a, fit_intercept=False)
ridge.fit(X, y)
coefs.append(ridge.coef_[0])
ax = plt.gca()
ax.plot(alphas, coefs)
ax.set_xscale('log')
handles, labels = ax.get_legend_handles_labels()
plt.legend(labels=df.columns[1:-1])
plt.xlabel('alpha')
plt.ylabel('weights')
plt.axis('tight')
plt.show()
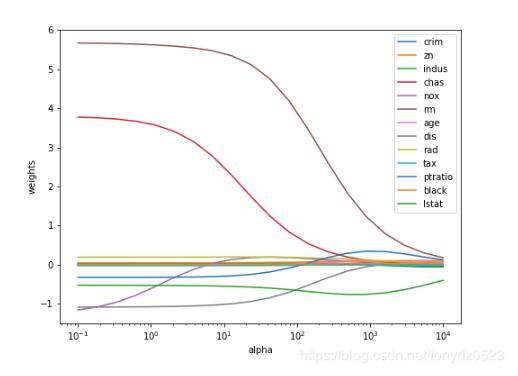
只有nox有些許波動。
# 主成分回歸進行回歸分析 pca_model = PCA() data_pca = pca_model.fit_transform(X) # 得到所有主成分方差 ratio_cumsum = np.cumsum(pca_model.explained_variance_ratio_) # 獲取方差占比超過0.8的索引值 rule_index = np.where(ratio_cumsum > 0.9) # 獲取最小的索引值 min_index = rule_index[0][0] # 根據最小索引值提取主成分 data_pca_result = data_pca[:, :min_index+1] # 建立回歸模型 model_liner = LinearRegression() # 訓練模型 model_liner.fit(data_pca_result, y) print(model_liner.coef_) #[[-0.02430516 -0.01404814]]
以上這篇python數據預處理 :數據共線性處理詳解就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。