溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
1、流程
大體流程如下,無論圖像、聲音、ADC數據都是如下流程:
(1)將原信號進行FFT;
(2)將進行FFT得到的數據去掉需要濾波的頻率;
(3)進行FFT逆變換得到信號數據;
2、算法仿真
2.1 生成數據:
#采樣點選擇1400個,因為設置的信號頻率分量最高為600Hz,根據采樣定理知采樣頻率要大于信號頻率2倍,所以這里設置采樣頻率為1400Hz(即一秒內有1400個采樣點) x=np.linspace(0,1,1400) #設置需要采樣的信號,頻率分量有180,390和600 y=2*np.sin(2*np.pi*180*x) + 3*np.sin(2*np.pi*390*x)+4*np.sin(2*np.pi*600*x)
2.2 對生成的數據進行FFT變換
yy=fft(y) #快速傅里葉變換 yf=abs(fft(y)) # 取模 yf1=abs(fft(y))/((len(x)/2)) #歸一化處理 yf2 = yf1[range(int(len(x)/2))] #由于對稱性,只取一半區間
2.3顯示轉換結果:
顯示原始FFT模值:
#混合波的FFT(雙邊頻率范圍)
plt.figure(2)
plt.plot(xf,yf,'r') #顯示原始信號的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意這里的顏色可以查詢顏色代碼表
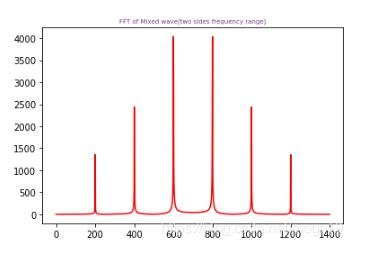
顯示原始FFT歸一化后的模值:
#混合波的FFT(歸一化)
plt.figure(3)
plt.plot(xf1,yf1,'g')
plt.title('FFT of Mixed wave(normalization)',fontsize=9,color='r')
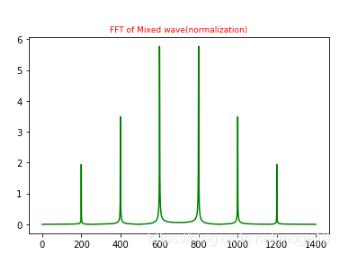
由于對稱,只取一半區間進行顯示
plt.figure(4)
plt.plot(xf2,yf2,'b')
plt.title('FFT of Mixed wave)',fontsize=10,color='#F08080')
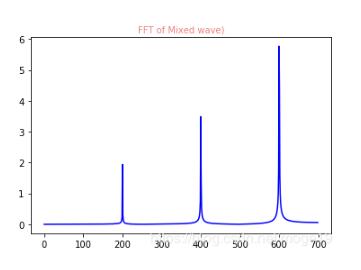
3、利用FFT進行濾波
例如將頻率為600HZ的噪聲濾掉,這里直接將該頻段的數據置零:
yy=fft(y) #快速傅里葉變換
yreal = yy.real # 獲取實數部分
yimag = yy.imag # 獲取虛數部分
test_y =yy
for i in range(len(yy)):
if i <=900 and i>=500:
test_y[i]=0
對置零后的數據進行逆變換:
test = np.fft.ifft(test_y) #對變換后的結果應用ifft函數,應該可以近似地還原初始信號。
對還原的數據進行FFT變換的結果:
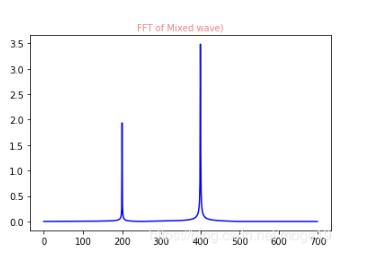
濾波后的數據和原數據相對比:
藍色的為原數據,橙色的為濾波后的數據
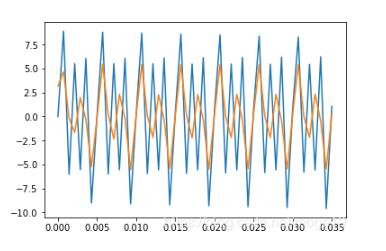
假設將400Hz和600Hz的信號都濾掉得到的信號圖像如下:
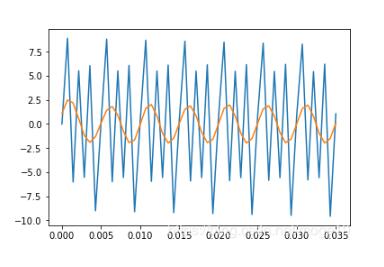
4、對隨機噪聲進行濾波
源碼:
noise_size = 1400
noise_array = np.random.normal(0, 2, noise_size)
adc_value=[]
for i in range(noise_size):
adc_value.append(0)
y= np.array(adc_value) + noise_array
yy=fft(y) #快速傅里葉變換
yf=abs(fft(y)) # 取模
yf1=abs(fft(y))/((len(y)/2)) #歸一化處理
yf2 = yf1[range(int(len(y)/2))] #由于對稱性,只取一半區間
#混合波的FFT(雙邊頻率范圍)
xf = np.arange(len(y))
plt.figure(1)
plt.plot(xf,yf,'r') #顯示原始信號的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意這里的顏色可以查詢顏色代碼表
yy=fft(y) #快速傅里葉變換
yreal = yy.real # 獲取實數部分
yimag = yy.imag # 獲取虛數部分
test_y =yy
for i in range(len(yy)):
if i <=1200 and i>=200:
test_y[i]=0
test = np.fft.ifft(test_y) #對變換后的結果應用ifft函數,應該可以近似地還原初始信號。
y=test
yy=fft(y) #快速傅里葉變換
yf=abs(fft(y)) # 取模
yf1=abs(fft(y))/((len(y)/2)) #歸一化處理
yf2 = yf1[range(int(len(y)/2))] #由于對稱性,只取一半區間
#混合波的FFT(雙邊頻率范圍)
xf = np.arange(len(y))
plt.figure(2)
plt.plot(xf,yf,'r') #顯示原始信號的FFT模值
plt.title('FFT of Mixed wave(two sides frequency range)',fontsize=7,color='#7A378B') #注意這里的顏色可以查詢顏色代碼表
運行結果:
原數據頻譜圖:
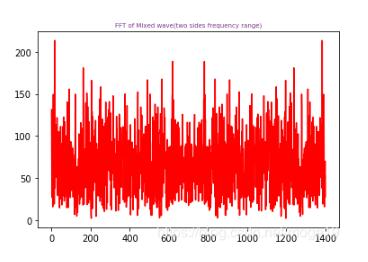
濾波后的頻譜圖:

濾波后(藍色線)與原數據(紅色線)對比:
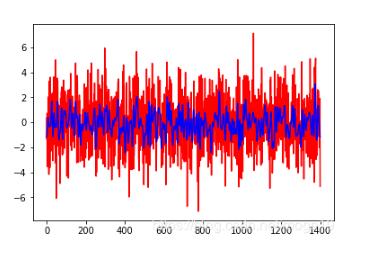
以上這篇Python利用FFT進行簡單濾波的實現就是小編分享給大家的全部內容了,希望能給大家一個參考,也希望大家多多支持億速云。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。