野生前端的數據結構練習（11）動態規劃算法

一.動態規劃算法

dynamic programming被認為是一種與遞歸相反的技術，遞歸是從頂部開始分解，通過解決掉所有分解出的問題來解決整個問題，而動態規劃是從問題底部開始，解決了小問題后合并為整體的解決方案，從而解決掉整個問題。

動態規劃在實現上基本遵循如下思路，根據邊界條件得到規模較小時的解，小規模問題合并時依據遞推關系式進行，也就是說較大規模的問題解可以由較小問題的解合并計算得到。最經典易懂的就是使用遞歸算法和動態規劃算法兩種不同的方式來計算斐波那契數列或求階乘的對比，動態規劃算法的特性相當于對計算過程進行了緩存，避免了不必要的重復計算。

本篇通過幾個典型的相關實例來學習和練習動態規劃算法。

二.尋找最長公共子串

題目不難理解，例如在單詞“raven”和“havoc”的最長公共子串就是av。最容易想到的算法就是暴力求解，也稱為貪心算法，在下一篇中會提供貪心算法暴力求解最長公共子串的示例代碼。

算法描述如下：

字符串1長為m,字符串2長為n,先生成一個m*n的矩陣L并將其中都填充為0，矩陣中的值L[x,y]表示如果存在公共字符串，那么該字符串在字符串1中的位置為從x-L[x,y]到x，在字符串2中的位置為從y-L[x,y]到y，換句話說：L[x,y]記錄了如果當前位置為公共子串的截止點時公共子串的長度。

遞推關系式如下:

若str1[x] === str2[y], L[x,y] = L[x-1,y-1] + 1;

若str1[x] !== str2[y], L[x,y] = 0;

從圖中可以更清晰地看到動態規劃算法在尋找公共子串時的過程：

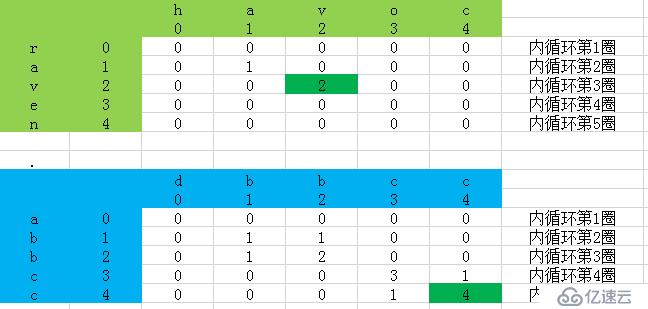
該表從左上角開始填空，循環遍歷每個格子，如果str1中的字符和str2中的某個字符相同，則需要找到其左上角格子的數字，然后加1填在自己的格子里，如果不相等則填0，最終記錄表中最大的值即為最長公共子串的結束位置，打印出最長公共子串也就很容易實現了。

參考代碼：

/**
 * 動態規劃求解最長公共子串
 */
function lcs(str1,str2) {
    let record = [];
    let max = 0;
    let pos = 0;
    let result = '';
    //初始化記錄圖
    for(let i = 0; i < str1.length; i++){
        record[i] = [];
        for(let j = 0; j < str2.length; j++){
            record[i][j] = 0;
        }
    }
    //動態規劃遍歷
    for(let i = 0; i < str1.length; i++){
        for(let j = 0; j < str2.length; j++){
            if (i === 0 || j === 0) {
                record[i][j] = 0;
            }else{
                if (str1[i] === str2[j]) {
                     record[i][j] = record[i-1][j-1] + 1;
                } else {
                     record[i][j] = 0;
                }
            }
            //更新最大值指針
            if (record[i][j] > max) {
                max = record[i][j];
                pos = [i];
            }
        }
    }
    //拼接結果
    if (!max) {
        return '';
    } else {
        for(let i = pos ; i > pos - max ; i--){
            result = str1[i] + result;
        }
        return result;
    }
}

console.log(lcs('havoc','raven'))
console.log(lcs('abbcc','dbbcc'))

三.0-1背包問題遞歸求解

0-1背包問題用遞歸或動態規劃都可以求解，通過本例和下一節的例子就可以對比兩種算法相反的求解過程。

背包問題是算法中一個經典的大類，從簡單到復雜一本書都講不完，本例中僅實現簡單的0-1背包問題，這類問題是指被放入背包的物品只能選擇放或者不放，不能只放入一部分。

0-1背包問題的描述是這樣的，假設保險箱中有n個物品，他們的尺寸存放在size[ ]數組中，每一個的價值存放在values[ ]數組中，你現在擁有一個背包，其容量為capacity，問應該裝哪些東西進背包，使得被裝入的物品總價值最大。

算法描述和遞推關系式如下:

1. 如果第n個物品無法放入背包，則最大價值等同于將其他物品放入背包時能得到的最大價值：

   maxValue = knapsack(capacity,size,values,n-1)

2. 如果第n個物品能夠放入背包，則最大價值等同于下列兩種情況中較大的一個：

   2.1 放入物品n,maxValue = knapsack(capacity - size[n], size, values, n-1)+values[n]

   2.2 不放物品n,maxValue = knapsack(capacity, size, values, n-1)

代碼實現如下：

/**
 * 遞歸求解0-1背包問題
 * 算法：
 * 1.如果單個物品體積超出背包容量，則肯定不拿
 * 2.如果單個物品體積未超出背包容量，則問題變為在下列兩種情況中取較大的值
 * 2.1 放入當前物品 knapsack(capacity - size[n-1], size, value, n-1) + value[n-1])
 * 2.2 不放入當前物品 knapsack(capacity, size, value, n-1) 
 */
function max(a,b) {
    return a>b?a:b;
}

/**
 * 
 * @param  {[type]} capacity 背包容量
 * @param  {[type]} size     物品體積數組
 * @param  {[type]} value    物品價值數組
 * @param  {[type]} n        物品個數
 * @return {[type]}          最大價值
 */
function knapsack(capacity, size, value, n) {
    //如果沒有物品或者背包容量為0 則無法增值

    if (n == 0 || capacity == 0 ) {
        return 0;
    }
    if (size[n-1] > capacity) {
        //算法步驟1 從最后一個物品開始，如果單個物品超出容量限制則不放入
        return knapsack(capacity, size, value, n-1);
    } else {
        //算法步驟2
        return max(knapsack(capacity - size[n-1], size, value, n-1) + value[n-1],knapsack(capacity, size, value, n-1));
    }
}

let value = [4,5,10,11,13];
let size = [3,4,7,8,9];
let capacity = 16;
let n = 5;

let result = knapsack(capacity, size, value, n);
console.log('result:',result);

可以看到代碼基本只是用程序語言實現了算法描述并進行了一些邊界條件的處理，并沒有進行任何實現方法上的優化，從它不斷調用自身就可以看出這是一個很明顯的遞歸方法。在遞歸方法下，由于重復訪問計算的問題，很難打印出最終到底選擇了哪些物品，而在下面的動態規劃算法的解法中就相對容易實現。

四.0-1背包問題動態規劃求解

動態規劃算法來求解0-1背包問題，核心遞推關系上并沒有什么差異，但正如開頭所講，動態規劃的優勢就是對計算過的結果進行了緩存，所以采用這個算法進行0-1背包問題求解得到最終結果后，可以再自頂向下反向查詢從緩存的表格中查出這個解的實現路徑，從而就可以判斷每個物品是否被選入當前解。

動態規劃算法實現如下：

/**
 * 動態規劃求解0-1背包問題
 */
function max(a,b) {
    return a>b?a:b;
}

/**
 * 
 * @param  {[type]} capacity 背包容量
 * @param  {[type]} size     物品體積數組
 * @param  {[type]} value    物品價值數組
 * @param  {[type]} n        物品個數
 * @return {[type]}          最大價值
 */
function knapsack(capacity, size, value, n) {
    //K[n][capacity]表示0~n-1這n個物品入選時的最優值
    let K = [];
    let pick = [];
    let result = 0;
    for (let i = 0; i <= n ; i++){
       K[i] = [];
       for(let j = 0; j <= capacity; j++){
          if(j === 0 || i === 0){
            //i=0為防御性編程，沒有實際意義
            //j=0表示背包容量為0，無法放入故結果為0
            K[i][j] = 0;
          } else if (size[i-1] > j){
            //如果背包容量比第i個物品的重量還小，則第i個物品必然無法放入，相當于前i-1個物品放入j容量背包時的最值
            K[i][j] = K[i-1][j];
          } else {
            //動態規劃解,當第i個物品可以放入時，K[i][j]等同于放入i時最值和不放i時的值取最大
            K[i][j] = max(K[i-1][j-size[i-1]] + value[i-1], K[i-1][j]);
          }
       }
    }
    result = K[n][capacity];

    //如何求解到底選了哪些物品?
    while(n > 0){
        if (K[n-1][capacity - size[n-1]] + value[n-1] > K[n-1][capacity]) {
            capacity -= size[n-1];
            n--;
            pick[n] = 1;
        } else {
            n--;
            pick[n] = 0;
        }
    }
    console.log('答案的選擇情況為:',pick);
    return result;
}

let value = [4,5,10,11,13];
let size = [3,4,7,8,9];
let capacity = 16;
let n = 5;

let result = knapsack(capacity, size, value, n);
console.log('結果:',result);