您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本文為原創作品,首發于微信公眾號:【坂本先生】,如需轉載請在文首明顯位置標明“轉載于微信公眾號:【坂本先生】”,否則追究其法律責任。
微信文章地址:實戰算法——多叉樹全路徑遍歷
本文研究的是如何對一個多叉樹進行全路徑的遍歷,并輸出全路徑結果。該問題的研究可以用在:Trie樹中查看所有字典值這個問題上。本文將對該問題進行詳細的模擬及進行代碼實現,討論了遞歸和非遞歸兩種方法優劣并分別進行實現,如果讀者對這兩種方法的優劣不感興趣可直接跳到問題構建章節進行閱讀。文章較長,推薦大家先收藏再進行閱讀。
這個問題知乎上已經有了很多答案,https://www.zhihu.com/question/20278387
在其基礎上我進行了一波總結:
將一個問題分解為若干相對小一點的問題,遇到遞歸出口再原路返回,因此必須保存相關的中間值,這些中間值壓入棧保存,問題規模較大時會占用大量內存。
執行效率高,運行時間只因循環次數增加而增加,沒什么額外開銷。空間上沒有什么增加
遞歸容易產生"棧溢出"錯誤(stack overflow)。因為需要同時保存成千上百個調用記錄,所以遞歸非常耗費內存。
遞歸擁有較好的代碼可讀性,對于數據量不算太大的運算,使用遞歸算法綽綽有余。
現在存在一個多叉樹,其結點情況如下圖,需要給出方法將葉子節點的所有路徑進行輸出。
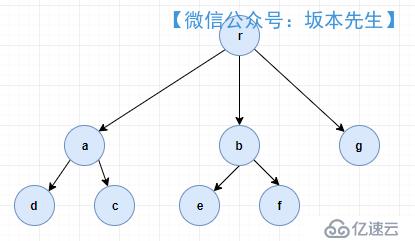
最終輸出結果應該有5個,即[rad,rac,rbe,rbf,rg]
首先我們對結點進行分析,構建一個結點類(TreeNode),然后我們需要有一個樹類(MultiTree),包含了全路徑打印的方法。最后我們需要建立一個Main方法進行測試。最終的項目結構如下:

注意:本文使用了lombok注解,省去了get,set及相關方法的實現。如果讀者沒有使用過lombok也可以自己編寫對應的get,set方法,后文會對每個類進行說明需要進行實現的方法,對核心代碼沒有影響。
TreeNode類
節點類,主要包含兩個字段:
該類中包含了必要的get,set方法,一個無參構造器,一個全參構造器
@Data
@RequiredArgsConstructor
@AllArgsConstructor
public class TreeNode {
private String content;
private HashMap<String,TreeNode> childs;
}MultiTree類
包含的字段只有兩個:
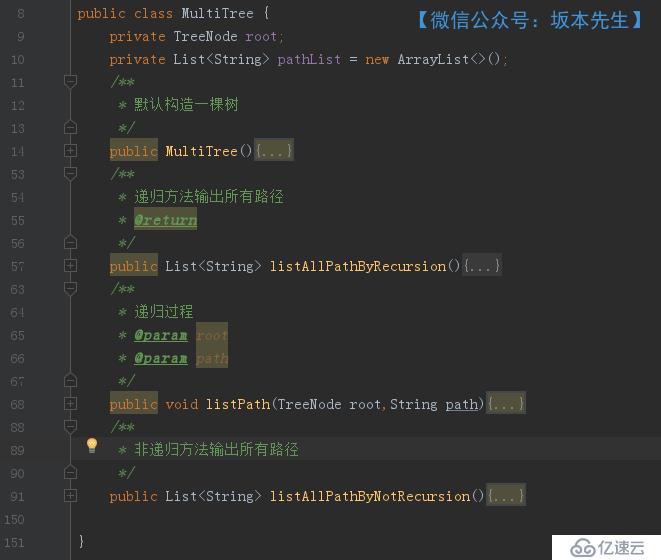
該類中的構造函數中我手動創建問題構建中的樹,相關代碼如下:
public MultiTree(){
//創建根節點
HashMap rootChilds = new HashMap();
this.root = new TreeNode("r",rootChilds);
//第一層子節點
HashMap aChilds = new HashMap();
TreeNode aNode = new TreeNode("a",aChilds);
HashMap bChilds = new HashMap();
TreeNode bNode = new TreeNode("b",bChilds);
HashMap gChilds = new HashMap();
TreeNode gNode = new TreeNode("g",gChilds);
//第二層結點
HashMap dChilds = new HashMap();
TreeNode dNode = new TreeNode("d",dChilds);
HashMap cChilds = new HashMap();
TreeNode cNode = new TreeNode("c",cChilds);
HashMap eChilds = new HashMap();
TreeNode eNode = new TreeNode("e",eChilds);
HashMap fChilds = new HashMap();
TreeNode fNode = new TreeNode("f",fChilds);
//建立結點聯系
rootChilds.put("a",aNode);
rootChilds.put("b",bNode);
rootChilds.put("g",gNode);
aChilds.put("d",dNode);
aChilds.put("c",cNode);
bChilds.put("e",eNode);
bChilds.put("f",fNode);
}在這個樹中,每個節點都有childs,如果是葉子節點,則childs中的size為0,這是下面判斷一個節點是否為葉子節點的重要依據接下來我們會對核心算法代碼進行實現。
Main類
public class Main {
public static void main(String[] args) {
MultiTree tree = new MultiTree();
List<String> path2 = tree.listAllPathByRecursion();
System.out.println(path2);
List<String> path3 = tree.listAllPathByNotRecursion();
System.out.println(path3);
}
}需要完善MultiTree類中的listAllPathByRecursion方法和listPath方法
遞歸過程方法:listAllPathByRecursion
算法流程圖如下:
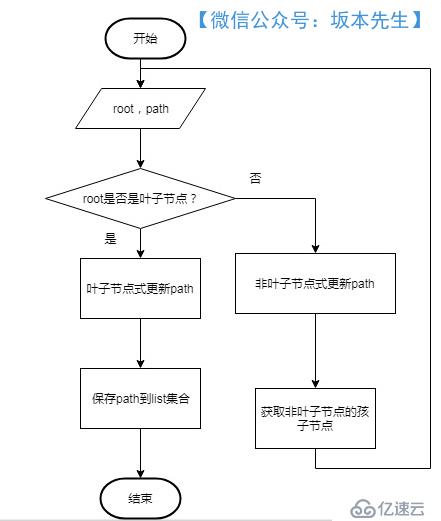
代碼實現如下:
public void listPath(TreeNode root,String path){
if(root.getChilds().isEmpty()){//葉子節點
path = path + root.getContent();
pathList.add(path); //將結果保存在list中
return;
}else{ //非葉子節點
path = path + root.getContent() + "->";
//進行子節點的遞歸
HashMap<String, TreeNode> childs = root.getChilds();
Iterator iterator = childs.entrySet().iterator();
while(iterator.hasNext()){
Map.Entry entry = (Map.Entry)iterator.next();
TreeNode childNode = (TreeNode) entry.getValue();
listPath(childNode,path);
}
}
}遞歸調用方法:listAllPathByRecursion
public List<String> listAllPathByRecursion(){
//清空路徑容器
this.pathList.clear();
listPath(this.root,"");
return this.pathList;
}非遞歸方法的代碼量和遞歸方法一比,簡直是太多了,而且內容不好理解,不知道大家能不能看懂我寫的代碼,我已經盡力寫上相關注釋了。
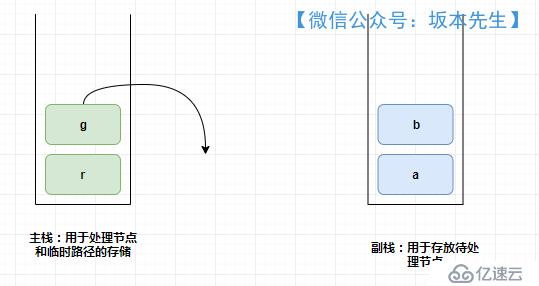
首先建立了兩個棧,示意圖如下,棧的實現使用Deque,需要注意的是代碼中的空指針情況。
主棧:用于處理節點和臨時路徑的存儲,主棧為空時說明,節點處理完畢
副棧:用于存放待處理節點,副棧為空時說明,節點遍歷完畢
其他相關變量介紹:
程序流程圖:
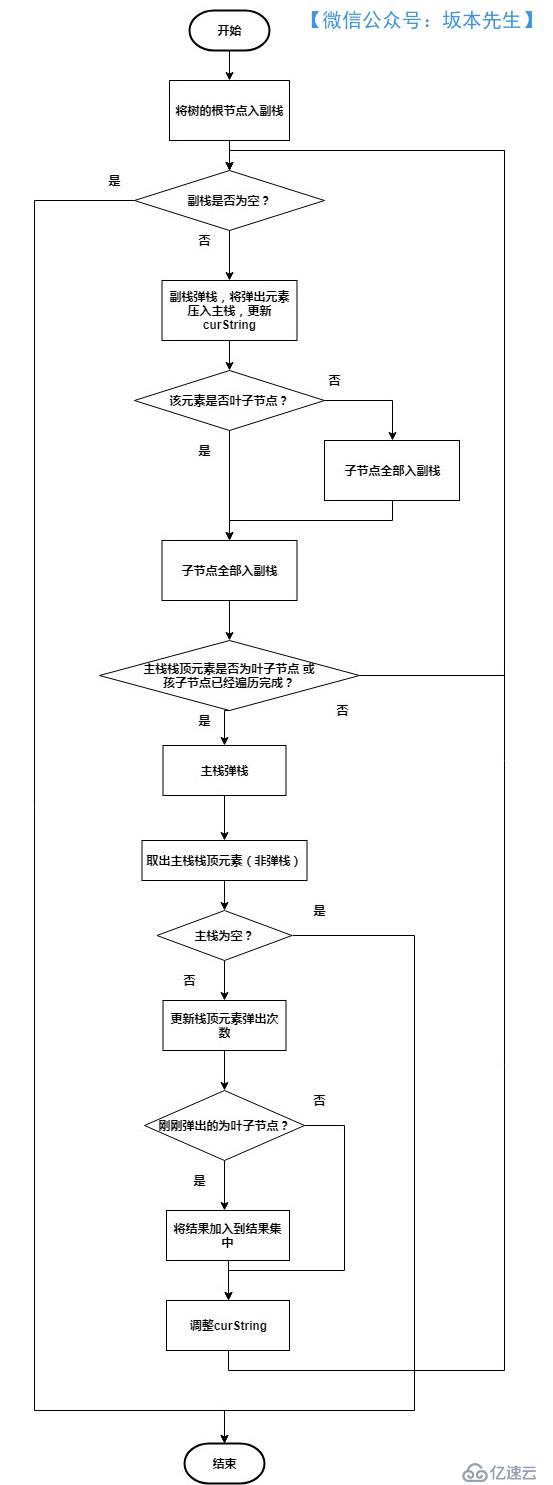
具體實現代碼如下:
/**
* 非遞歸方法輸出所有路徑
*/
public List<String> listAllPathByNotRecursion(){
//清空路徑容器
this.pathList.clear();
//主棧,用于計算處理路徑
Deque<TreeNode> majorStack = new ArrayDeque();
//副棧,用于存儲待處理節點
Deque<TreeNode> minorStack = new ArrayDeque();
minorStack.addLast(this.root);
HashMap<String,Integer> popCount = new HashMap<>();
String curString = "";
while(!minorStack.isEmpty()){
//出副棧,入主棧
TreeNode minLast = minorStack.pollLast();
majorStack.addLast(minLast);
curString+=minLast.getContent()+"->";
//將該節點的子節點入副棧
if(!minLast.getChilds().isEmpty()){
HashMap<String, TreeNode> childs = minLast.getChilds();
Iterator iterator = childs.entrySet().iterator();
while(iterator.hasNext()){
Map.Entry entry = (Map.Entry)iterator.next();
TreeNode childNode = (TreeNode) entry.getValue();
minorStack.addLast(childNode);
}
}
//出主棧
TreeNode majLast = majorStack.peekLast();
//循環條件:棧頂為葉子節點 或 棧頂節點孩子節點遍歷完了(需要注意空指針問題)
while(majLast.getChilds().size() ==0 ||
(popCount.get(majLast.getContent())!=null && popCount.get(majLast.getContent()).equals(majLast.getChilds().size()))){
TreeNode last = majorStack.pollLast();
majLast = majorStack.peekLast();
if(majLast == null){ //此時主棧為空,運算完畢
return this.pathList;
}
if(popCount.get(majLast.getContent())==null){//第一次彈出孩子節點,彈出次數設為1
popCount.put(majLast.getContent(),1);
}else{ //非第一次彈出孩子節點,在原有基礎上加1
popCount.put(majLast.getContent(),popCount.get(majLast.getContent())+1);
}
String lastContent = last.getContent();
if(last.getChilds().isEmpty()){//如果是葉子節點才將結果加入路徑集中
this.pathList.add(curString.substring(0,curString.length()-2));
}
//調整當前curString,減去2是減的“->”這個符號
curString = curString.substring(0,curString.length()-lastContent.length()-2);
}
}
return this.pathList;
}調用Main類中的main方法,得到執行結果,和預期結果相同,代碼通過測試
listAllPathByRecursion[r->a->c, r->a->d, r->b->e, r->b->f, r->g]
listAllPathByNotRecursion[r->g, r->b->f, r->b->e, r->a->d, r->a->c]其實該文章是我在研究《基于Trie樹的敏感詞過濾算法實現》的一個中間產物,其實原來應該也實現過多叉樹的路徑遍歷問題,但是因為時間原因加之原來沒有較好的知識管理系統,代碼和筆記都丟了,今天趁機再進行一波總結。希望該文章能夠幫助到需要的人。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。