您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
1、二叉搜索樹
(1)、逼近折半查找的查找算法;
(2)、一般不允許出現重復數字,不然沒法存儲;
(3)、滿足:左孩子數據 < 根結點數據 < 右孩子數據;根(父)結點比左孩子的大,比右孩子的小;
(4)左子樹和右子樹也是二叉搜索樹;
2、為什么叫二叉搜索樹?
如果對一顆二叉搜索樹進行中序遍歷,可以按從小到大的順序輸出,此時又叫做二叉排序樹。
如圖:
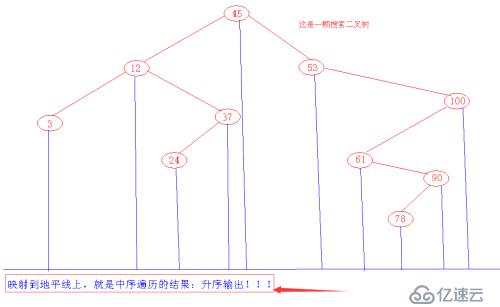
3、搜索二叉樹上的操作
全部用C++實現的。
(1)、之前學習二叉樹,并沒有說什么插入,刪除操作,那是因為,沒有規律而言,怎么進行操作呢?搜索二叉樹的規律如此明顯,那么插入,刪除必是重中之中!
(2)、我們輸入相同的數字,但是順序不同的話,生成的搜索二叉樹是不一樣的!
例:int ar[] = {3, 7, 9, 1, 0, 6, 4, 2,}; 和int ar[] = {7, 3, 9, 1, 0, 6, 4, 2,}; 生成的搜索二叉樹不一樣。
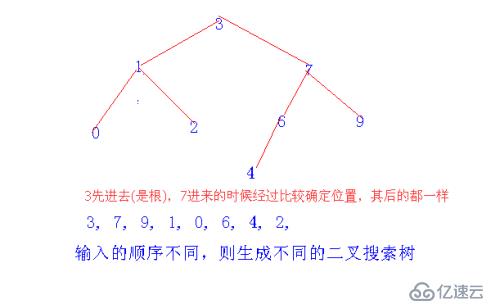
(3)插入函數:
重分利用搜索二叉樹的性質:
void insert(BSTreeNode<Type> *&t, const Type &x){
if(t == NULL){
t = new BSTreeNode<Type>(x);
return;
}else if(x < t->data){
insert(t->leftChild, x);
}else if(x > t->data){
insert(t->rightChild, x);
}else{
return;
}
}(4)、刪除函數:
思想:要刪除一個有左孩子或右孩子或是葉子結點,看成一種情況,做法:保存要刪除的結點,因為傳的是引用,可以直接修改上一個結點的左孩子或右孩子,使其跨過當前的直指下一個結點,在釋放當前的結點空間。
第二種情況:就是要刪除的既有左子樹,又有右子樹,此時可以有兩種做法:i>找左子樹最大的數字,覆蓋要刪除的數字,在往左子樹找這個數字刪除-->遞歸!ii>找右子樹最小的數字,覆蓋要刪除的數字,在往右子樹找這個數字刪除-->遞歸!
第一種情況圖形想法如下:
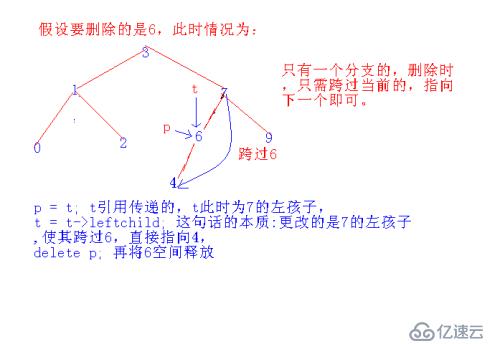
刪除左邊和刪除右邊,還有是葉子結點,想法一樣。
第二種情況圖形想法如下:
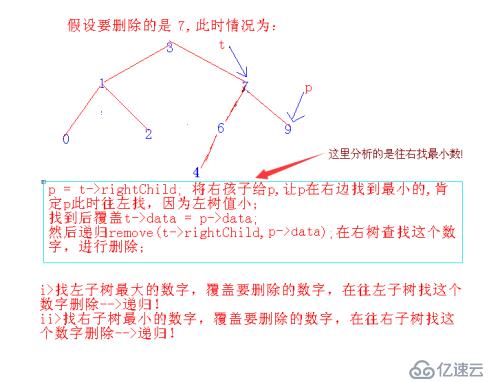
代碼如下:
bool remove(BSTreeNode<Type> *&t, const Type &key){
if(t == NULL){ //t傳的是引用,每次可以進行直接更改!
return false;
}
if(key < t->data){
remove(t->leftChild, key);
}else if(key > t->data){
remove(t->rightChild, key);
}else{
if(t->leftChild != NULL && t->rightChild != NULL){ //第二種情況
BSTreeNode<Type> *p = t->rightChild;
while(p->leftChild != NULL){
p = p->leftChild;
}
t->data = p->data;
remove(t->rightChild, p->data); //在右樹找p->data的數字進行刪除;
}else{ //第一種情況
BSTreeNode<Type> *p = t;
if(t->leftChild == NULL){
t = t->rightChild; //引用的好處體現出來了;
}else{
t = t->leftChild; //引用的好處體現出來了;
}
delete p;
}
}
return true;
}
/* 以下這個代碼是先想到的,比較容易,上面這個是經過思考的,將三種情況看成一種情況來處理。
bool remove(BSTreeNode<Type> *&t, const Type &key){
if(t == NULL){
return false;
}
if(key < t->data){
remove(t->leftChild, key);
}else if(key > t->data){
remove(t->rightChild, key);
}else{ //以下三種情況可以看成一種;
if(t->leftChild == NULL && t->rightChild == NULL){
delete t;
t = NULL;
}else if(t->leftChild != NULL && t->rightChild == NULL){
BSTreeNode<Type> *p = t;
t = t->leftChild;
delete p;
}else if(t->leftChild == NULL && t->rightChild != NULL){
BSTreeNode<Type> *p = t;
t = t->rightChild;
delete p;
}else{
BSTreeNode<Type> *p = t->rightChild;
while(p->leftChild != NULL){
p = p->leftChild;
}
t->data = p->data;
remove(t->rightChild, p->data);
}
}
return true;
}
*/4、搜索二叉樹的完整代碼、測試代碼、測試結果
(1)、完整代碼:
#ifndef _BSTREE_H_
#define _BSTREE_H_
#include<iostream>
using namespace std;
#define MIN_NUMBER -8937589
#define MAX_NUMBER 99999999
template<typename Type>
class BSTree;
template<typename Type>
class BSTreeNode{
friend class BSTree<Type>;
public:
BSTreeNode() : data(Type()), leftChild(NULL), rightChild(NULL){}
BSTreeNode(Type d, BSTreeNode *left = NULL, BSTreeNode *right = NULL)
: data(d), leftChild(left), rightChild(right){}
~BSTreeNode(){}
private:
Type data;
BSTreeNode *leftChild;
BSTreeNode *rightChild;
};
template<typename Type>
class BSTree{
public:
BSTree() : root(NULL){}
BSTree<Type>& operator=(const BSTree &bst){
if(this != &bst){
root = copy(bst.root);
}
return *this;
}
~BSTree(){}
public:
void insert(const Type &x){
insert(root, x);
}
void inOrder()const{
inOrder(root);
}
Type Min()const{
return Min(root);
}
Type Max()const{
return Max(root);
}
BSTreeNode<Type>* find(const Type &key)const{
return find(root, key);
}
BSTreeNode<Type> *copy(const BSTreeNode<Type> *t){
if(t == NULL){
return NULL;
}
BSTreeNode<Type> *tmp = new BSTreeNode<Type>(t->data);
tmp->leftChild = copy(t->leftChild);
tmp->rightChild = copy(t->rightChild);
return tmp;
}
BSTreeNode<Type>* parent(const Type &key)const{
return parent(root, key);
}
bool remove(const Type &key){
return remove(root, key);
}
protected:
bool remove(BSTreeNode<Type> *&t, const Type &key){
if(t == NULL){ //重點:傳的是引用
return false;
}
if(key < t->data){
remove(t->leftChild, key);
}else if(key > t->data){
remove(t->rightChild, key);
}else{
if(t->leftChild != NULL && t->rightChild != NULL){
BSTreeNode<Type> *p = t->rightChild;
while(p->leftChild != NULL){
p = p->leftChild;
}
t->data = p->data;
remove(t->rightChild, p->data);
}else{
BSTreeNode<Type> *p = t;
if(t->leftChild == NULL){
t = t->rightChild; //可以直接更改左右孩子
}else{
t = t->leftChild; //可以直接更改左右孩子
}
delete p;
}
}
return true;
}
/*
bool remove(BSTreeNode<Type> *&t, const Type &key){
if(t == NULL){
return false;
}
if(key < t->data){
remove(t->leftChild, key);
}else if(key > t->data){
remove(t->rightChild, key);
}else{ //以下三種情況可以看成一種;
if(t->leftChild == NULL && t->rightChild == NULL){
delete t;
t = NULL;
}else if(t->leftChild != NULL && t->rightChild == NULL){
BSTreeNode<Type> *p = t;
t = t->leftChild;
delete p;
}else if(t->leftChild == NULL && t->rightChild != NULL){
BSTreeNode<Type> *p = t;
t = t->rightChild;
delete p;
}else{
BSTreeNode<Type> *p = t->rightChild;
while(p->leftChild != NULL){
p = p->leftChild;
}
t->data = p->data;
remove(t->rightChild, p->data);
}
}
return true;
}*/
BSTreeNode<Type>* parent(BSTreeNode<Type> *t, const Type &key)const{
if(t == NULL || t->data == key){
return NULL;
}
if(t->leftChild->data == key || t->rightChild->data == key){
return t;
}
if(key < t->data){
return parent(t->leftChild, key);
}else{
return parent(t->rightChild, key);
}
}
BSTreeNode<Type>* find(BSTreeNode<Type> *t, const Type &key)const{
if(t == NULL){
return NULL;
}
if(t->data == key){
return t;
}else if(key < t->data){
return find(t->leftChild, key);
}else{
return find(t->rightChild, key);
}
}
Type Max(BSTreeNode<Type> *t)const{
if(t != NULL){
while(t->rightChild){
t = t->rightChild;
}
return t->data;
}
return MAX_NUMBER;
}
Type Min(BSTreeNode<Type> *t)const{
if(t != NULL){
while(t->leftChild){
t = t->leftChild;
}
return t->data;
}
return MIN_NUMBER;
}
void inOrder(BSTreeNode<Type> *t)const{
if(t != NULL){
inOrder(t->leftChild);
cout<<t->data<<" ";
inOrder(t->rightChild);
}
}
void insert(BSTreeNode<Type> *&t, const Type &x){
if(t == NULL){
t = new BSTreeNode<Type>(x);
return;
}else if(x < t->data){
insert(t->leftChild, x);
}else if(x > t->data){
insert(t->rightChild, x);
}else{
return;
}
}
private:
BSTreeNode<Type> *root;
};
#endif(2)測試代碼:
#include"bstree.h"
int main(void){
int ar[] = {3, 7, 9, 1, 0, 6, 4, 2,};
int n = sizeof(ar) / sizeof(int);
BSTree<int> bst;
for(int i = 0; i < n; i++){
bst.insert(ar[i]);
}
bst.inOrder();
cout<<endl;
cout<<bst.Min()<<endl;
cout<<bst.Max()<<endl;
BSTreeNode<int> *p = bst.find(6);
BSTreeNode<int> *q = bst.parent(4);
printf("%p %p\n", p, q);
bst.remove(0);
bst.inOrder();
cout<<endl;
return 0;
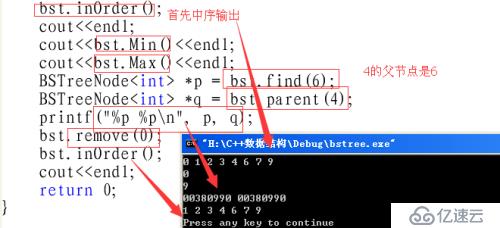
}(3)、測試結果:
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。