編程開發中二叉樹和霍夫曼樹的示例分析

小編給大家分享一下編程開發中二叉樹和霍夫曼樹的示例分析，相信大部分人都還不怎么了解，因此分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后大有收獲，下面讓我們一起去了解一下吧！

一、二叉樹的深層性質

性質1
在二叉樹的第 i層最多有 2^(i-1)個結點 。 (i≥1)
?第一層最多有 2-1=1個結點
?第二層最多有 2^(2-1)=2個結點
?第三層最多有 2^(3-1)=4個結點
性質2
深度為 k 的二叉樹最多有 2^k -1個結點 。 (k  ≥ 0)
?如果有一層 ，最多有  1=2- 1=1 個結點
?如果有兩層 ，最多有  1+2=2^2- 1=3 個結點
?如果有三層 ，最多有  1+2+4=2^3 -1=7個結點
性質3
對任何一棵二叉樹 ， 如果其葉結點有 n0個 ， 度為2的非葉結點有n2個， 有 則有
?n0＝n2＋1
性質4
具有n個結點的完全二叉樹的高度為[log2 n]+ 1  。 （[X]表示不大于  X  的最大整數)
性質5
一棵有 n個結點的二叉樹 （ 高度為[log2 n]+ 1）， 按層次對結點進行編號（ 從上到下 ， 從左到右 ），對任意結點 i 有 ：
?如果  i = 1 ， 則結點 i 是二叉樹的根
?如果  i > 1 ， 則其雙親結點為 [ i/2]
?如果  2i <= n ，則結點  i 的左孩子為  2i
?如果  2i > n  ， 則結點 i 無左孩子
?如果  2i+1 <= n  ，則結點  i  為 的右孩子為  2i+1
?如果  2i+1 > n , 則結點 i無右孩子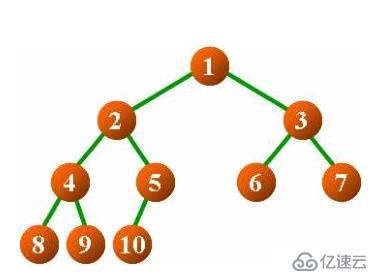

二、創建二叉樹的方法

指路法定位結點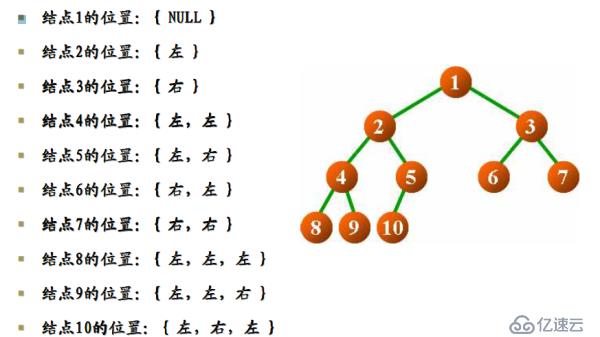

指路法通過根結點與目標結點的相對位置進行定位
指路法可以避開二叉樹遞歸的性質“線性”定位

二叉樹存儲結構

用結構體來定義二叉樹中的指針域
二叉樹的頭結點也可以用結構體實現

 //結點指針域定義
typedef struct _tag_BTreeNode BTreeNode;
struct _tag_BTreeNode
{
    BTreeNode* left;
    BTreeNode* right;   
};                             

//頭結點定義
typedef struct _tag_BTree TBTree;
struct  _tag_BTree
{
    int count;
    BTreeNode* root;
};

定位：利用二進制中的0和1分別表示left和right，位運算是實現指路法的基礎

三、遍歷二叉樹

單鏈表的遍歷是指從第一個結點開始（下標為0的結點），按照某種次序依次訪問每一個結點。
二叉樹的遍歷是指從根結點開始，按照某種次序依次訪問二叉樹中的所有結點。
前序遍歷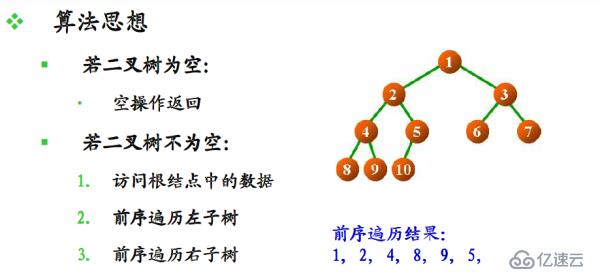

中序遍歷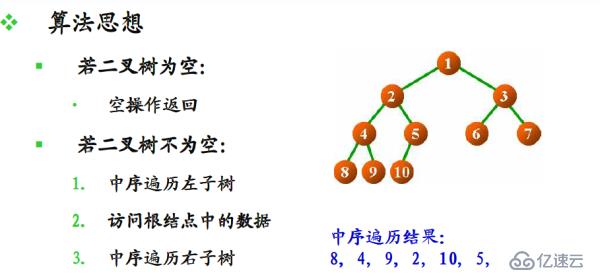

后序遍歷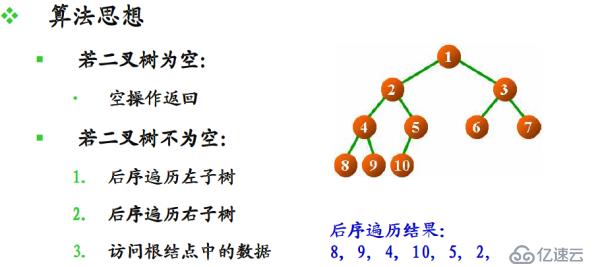

層次遍歷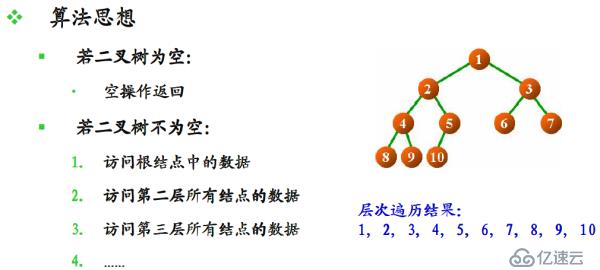

四、線索化二叉樹

線索化二叉樹指的是將二叉樹中的結點進行邏輯意義上的“重排列”，使其可以線性的方式訪問每一個結點
二叉樹線索化之后每個結點都有一個線性下標，通過這個下標可以快速訪問結點，而不需要遍歷二叉樹
線索化方法1
&emsp;利用結點中的空指針域，使其指向后繼結點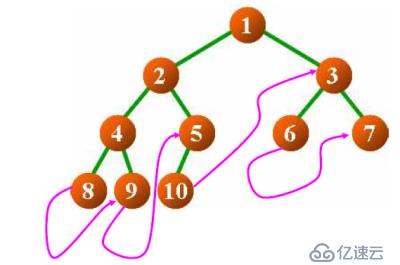

算法思想：

線索化方法2
&emsp;利用線性表保存二叉樹的遍歷順序

算法思想：

利用結點空指針線索化的方法會破壞樹的結構，線索化二叉樹之后不能夠再恢復
這兩個問題可以在樹結點中加入一個線索化指針而得以解決
&emsp;然而線索化指針的加入又會浪費內存空間，不夠靈活
&emsp;鏈表線索化方法不會破化樹的結構，不需要時線索化時銷毀鏈表即可
鏈表線索化方法可以很容易的以任何一種遍歷順序對二叉樹進行線索化

五、霍夫曼樹

以上是“編程開發中二叉樹和霍夫曼樹的示例分析”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！