溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
html5 canvas bezierCurveTo涉及4個點:o(開始點),cp1(控制點1),cp2(控制點2),p(結束點)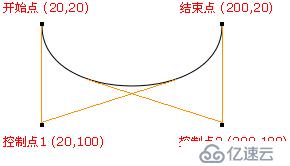
當 o到p的走向(向量op)和cp1到cp2的走向(向量c12)相反時,就會出現打結的情況,我采取降級處理的方法,即發現會打結時,改為使用lineTo:
p = parts[i][j]; var o = parts[i][j-1]; //p前面一點 var cp1 = cps[2*(j-1)]; var cp2 = cps[2*j-1]; var op = p.subtract(o),c12=cp2.subtract(cp1); //繞過打結問題 if(op.x*c12.x+op.y*c12.y>0) //控制點走向和折線走向一致 ctx.bezierCurveTo(cp1.x,cp1.y, cp2.x,cp2.y, p.x, p.y); else ctx.lineTo(p.x,p.y);
向量夾角公式:
cosθ=向量a×向量b/|向量a|×|向量b| = (x1x2+y1y2)/[√(x12+y12)√(x22+y22)]
我將兩向量夾角大于90度判定為兩向量反向,
當180>θ>90時cosθ<0,夾角公式分母總為正,所以只要判定分子的正負即可。
過特征點平滑效果,可參考:
https://blog.csdn.net/u011284073/article/details/81385922
控制點的計算過程可以參考 http://turfjs.org/docs#bezierSpline 的源碼,中點連線平移得到控制點,其使用的方法即:https://blog.csdn.net/ch_soft/article/details/7401582
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。