您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
本篇內容介紹了“C語言浮點型數據在內存中的存儲方式是什么”的有關知識,在實際案例的操作過程中,不少人都會遇到這樣的困境,接下來就讓小編帶領大家學習一下如何處理這些情況吧!希望大家仔細閱讀,能夠學有所成!
咱們先上一盤開胃菜,試試看叭
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
return 0;
}路飛:請問打印出來都是什么結果呢?貝吉塔:簡單,喏

路飛:哈哈~雖然很符合直觀想法,但是錯啦錯啦,喏
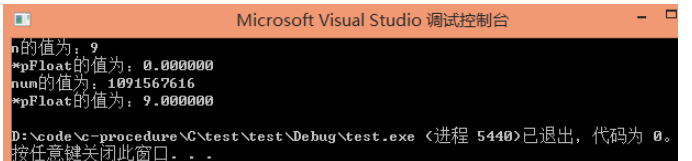
貝吉塔:蛤??!這么奇怪的結果
既然上述結果跟我們所理解的整型數據存儲方式的結果不同,這就說明浮點型數據在內存中的存儲方式是不一樣滴~
詳細解讀:
根據國際標準IEEE(電氣和電子工程協會)754,任意一個二進制浮點數V可以表示成下面的形式:
(-1)^S * M * 2^E
(-1)^S表示符號位。當S=0,V為正數;當S=1,V為負數
M表示有效數字,大于等于1,小于2
2^E表示指數位
舉例來說:
十進制的5.5,寫成二進制是101.1,相當于(1)^0 * 1.011 * 2^2,此時
| aiphabet | Value |
|---|---|
| S | 0 |
| M | 1.011 |
| E | 2 |
此時會有鐵汁有疑問,為什么5.5的二進制是101.1??不應該是101.101嗎?
我們看看下圖,假如是101.101,那么轉換成十進制就是5.625,因為二進制每一位的權重都不同,不能想當然

假如說給的十進制是5.3,那么這個0.3是不能精確表示的,所以說浮點數容易丟失精度
對于32位的浮點數(float),最高的1位是符號位S,接著的8位是指數E,剩下的23位是有效數字M
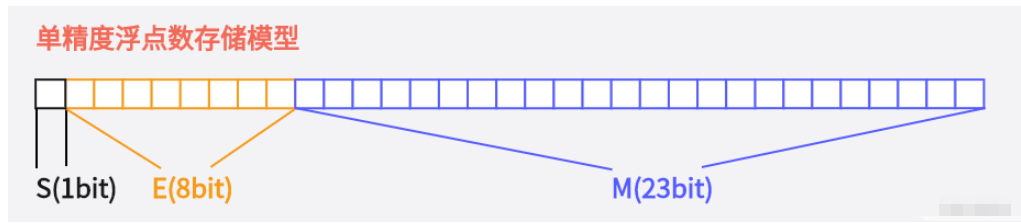
對于64位的浮點數(double),最高的1位是符號位S,接著的11位是指數E,剩下的52位是有效數字M
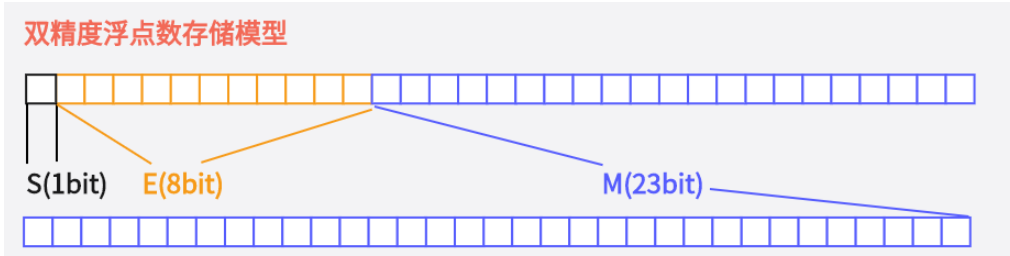
前面說過,1≤M<2,也就是說,M可以攜程1.xxxxxx的形式。其中xxxxxx表示小數部分
IEEE 754規定,在計算機內部保存M時,默認這個數的第一位總是1,因此可以被舍去,只保存后面的xxxxxx。比如保存1.01時,只保存01,等到讀取的時候再放回去,這樣做的目的是節省空間
首先,E為一個無符號整數(unsigned int),這意味著,如果E為8位,它的取值范圍為0-255;如果E為11位,它的取值范圍為0-2047。
但是我們知道,科學計數法中的E是可以出現負數的,所以IEEE 754規定,存入內存時E的真實值必須再加上一個中間數
對于8位的E,中間數取127;對于11位的E,中間數取1023。
比如2^10的E是10,所以保存成32位浮點數時,必須保存成10+127=137,即為10001001
int main()
{
float f = 5.5f;
//(-1)^0 * 1.011 * 2^2
//S = 0
//M = 1.011
//E = 2
//這樣存: 0 10000001 01100000000000000000000
//也就是: 0100 0000 1011 0000 0000 0000 0000 0000
//十六進制表示: 40 b0 00 00
return 0;
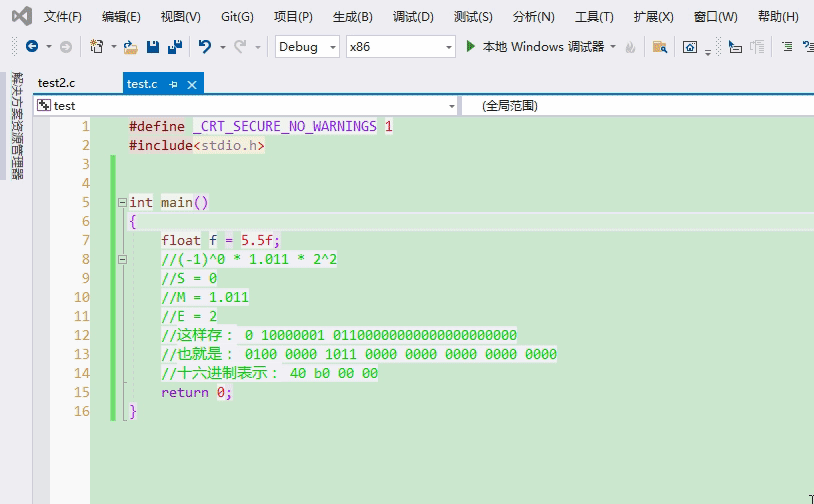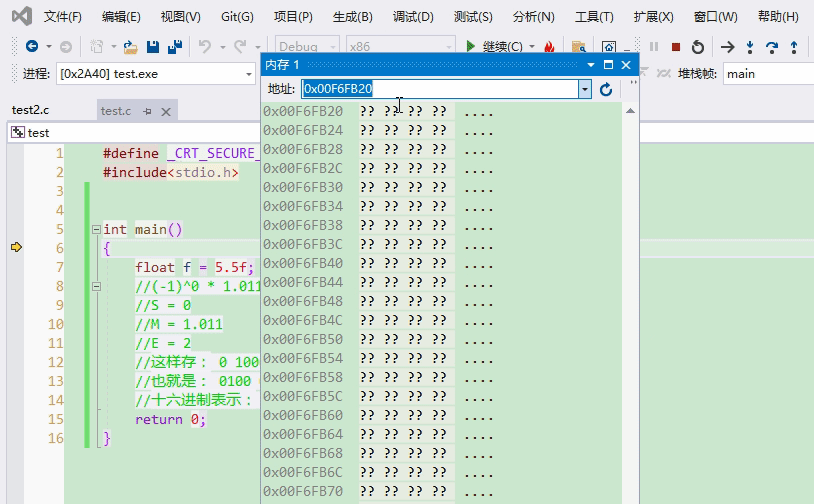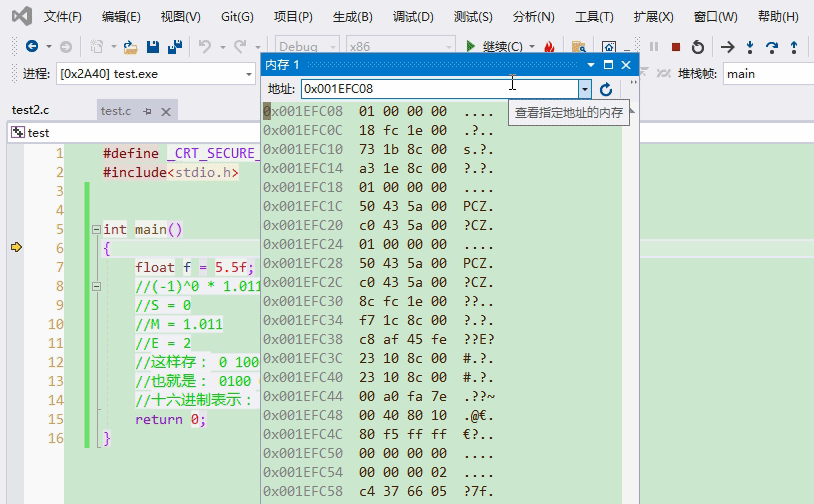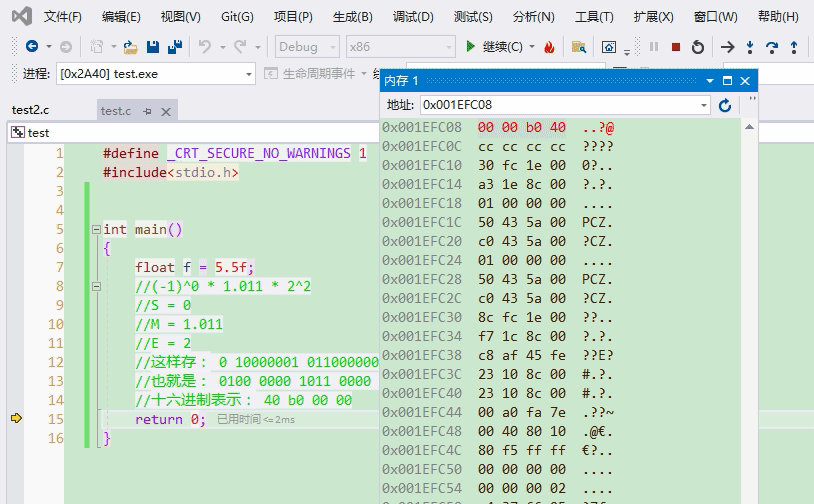
}5.5按float存儲,如圖所示
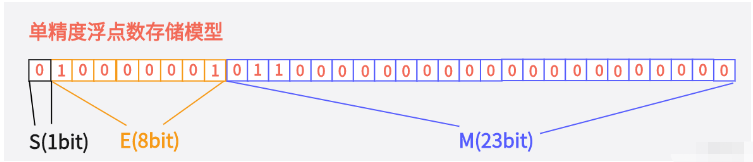
轉換成十六進制就是40 b0 00 00,咱們調試看看叭~因為VS是小端字節序存儲,所以地址由低到高看到的是00 00 b0 40
S和M的取出很簡單,原樣返回,但是E我就得仔細談談了
E不全為0或不全為1:
這時,把E減去之前加上去的127(或1023),得到真實值,再講有效數字M前加上第一位的1,這種情況最簡單,逆著來就是了
E為全0:
這時真實的E為-127(或-1023),太小了,所以規定浮點數的指數E等于1-127(或1-1023)即為真實值,有效數字M不再加上第一位的1,而是還原為0.xxxxxx的小數。這樣做是為了表示±0,以及接近于0的很小的數字(這是規定,大家不要糾結)
E為全1:
這時真實的E為128,太大了,如果有效數字M全為0,表示±無窮大(正負取決于符號位S)
我們回到最開始的代碼,看看能不能解決啦
#include<stdio.h>
int main()
{
int n = 9;
float* pFloat = (float*)&n;
printf("n的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
*pFloat = 9.0;
printf("num的值為:%d\n", n);
printf("*pFloat的值為:%f\n", *pFloat);
return 0;
}答案:
先分析前兩個輸出:
首先,9是int類型的,存儲按整型存儲規則,就是在內存中都是以補碼形式存放的,而正數的原碼、反碼、補碼都一樣
| int | 9 |
|---|---|
| 原碼 | 00000000000000000000000000001001 |
| 反碼 | 00000000000000000000000000001001 |
| 補碼 | 00000000000000000000000000001001 |
2.第一個輸出是以%d(十進制整型)輸出,所以輸出結果確實是9
3. 第二個輸出,pFloat指針認為數據是以單精度浮點數類型存儲的,所以解應用的時候也是這么做的。此時pFloat發現E全為0,按照上述規則,9取出來就變成0.000000000000000000001001 * 2^-126,即使不管后面的指數!有效數字都已經非常小了!所以打印出來小數點后6位看到的是0.000000

然后,分析后兩個輸出:
首先,9.0是float類型的,存儲按浮點數存儲規則,即為(-1)^0 * 1.001 * 2^3
| float | 9.0 |
|---|---|
| S | 0 |
| M | 1.001 |
| E | 3 |
存到內存里就是:

于是第三個輸出,%d把它當整型輸出,那么在整型眼里,直接把這32位直接轉成十進制輸出了,就造成了輸出結果為1091567616
而第四個輸出就是按float類型輸出的,所以結果就是9.000000
“C語言浮點型數據在內存中的存儲方式是什么”的內容就介紹到這里了,感謝大家的閱讀。如果想了解更多行業相關的知識可以關注億速云網站,小編將為大家輸出更多高質量的實用文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。