C++怎么把二叉搜索樹轉換累加樹

今天小編給大家分享一下C++怎么把二叉搜索樹轉換累加樹的相關知識點，內容詳細，邏輯清晰，相信大部分人都還太了解這方面的知識，所以分享這篇文章給大家參考一下，希望大家閱讀完這篇文章后有所收獲，下面我們一起來了解一下吧。

把二叉搜索樹轉換為累加樹

給出二叉 搜索 樹的根節點，該樹的節點值各不相同，請你將其轉換為累加樹（Greater Sum Tree），使每個節點 node 的新值等于原樹中大于或等于 node.val 的值之和。

提醒一下，二叉搜索樹滿足下列約束條件：

• 節點的左子樹僅包含鍵 小于 節點鍵的節點。

• 節點的右子樹僅包含鍵 大于 節點鍵的節點。

• 左右子樹也必須是二叉搜索樹。

示例 1：

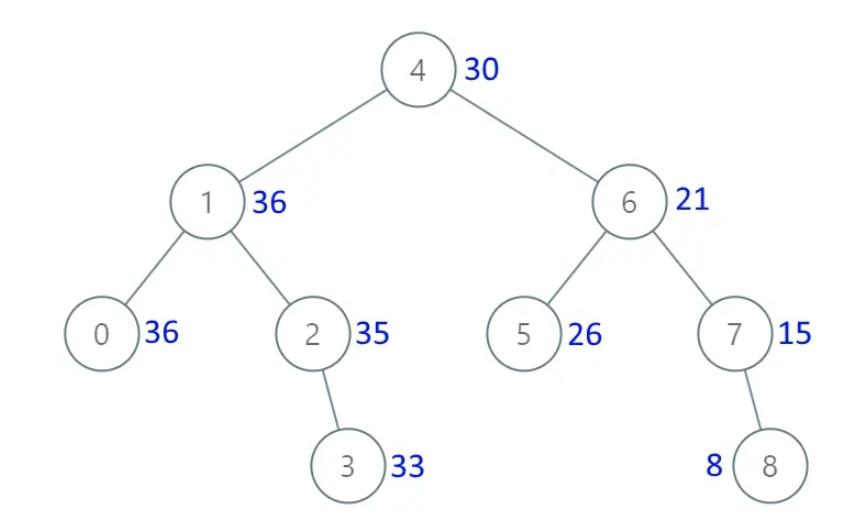
輸入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
輸出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

輸入：root = [0,null,1]
輸出：[1,null,1]

示例 3：

輸入：root = [1,0,2]
輸出：[3,3,2]

示例 4：

輸入：root = [3,2,4,1]
輸出：[7,9,4,10]

提示：

方法一：DFS反向中序遍歷

二叉搜索樹有一個非常不錯的性質，就是“中序遍歷所經過的節點的值是非遞減的”。

同理，如果我們“反向中序遍歷（右子->根->左子）”一顆二叉搜索樹，那么我們的遍歷順序就是“非遞增”的。

我們只需要記錄一下“歷史遍歷節點的總和”，然后按照反向中序遍歷的方式去遍歷這棵二叉樹，遍歷到某個節點時，將這個節點的值修改為“這個節點的初始值 和 歷史節點總和 的 和”，同時更新“歷史遍歷節點的總和”即可。

• 時間復雜度O(n)，其中nnn是二叉樹節點的個數

• 空間復雜度O(n)

AC代碼

C++

class Solution {
private:
    int total;

    void dfs(TreeNode* root) {
        if (!root)
            return;
        dfs(root->right);
        total = root->val = total + root->val;
        dfs(root->left);
    }
public:
    Solution() {total = 0;}

    TreeNode* convertBST(TreeNode* root) {
        dfs(root);
        return root;
    }
};

以上就是“C++怎么把二叉搜索樹轉換累加樹”這篇文章的所有內容，感謝各位的閱讀！相信大家閱讀完這篇文章都有很大的收獲，小編每天都會為大家更新不同的知識，如果還想學習更多的知識，請關注億速云行業資訊頻道。