Java二叉樹查詢原理實例代碼分析

這篇文章主要介紹“Java二叉樹查詢原理實例代碼分析”，在日常操作中，相信很多人在Java二叉樹查詢原理實例代碼分析問題上存在疑惑，小編查閱了各式資料，整理出簡單好用的操作方法，希望對大家解答”Java二叉樹查詢原理實例代碼分析”的疑惑有所幫助！接下來，請跟著小編一起來學習吧！

二叉查詢樹

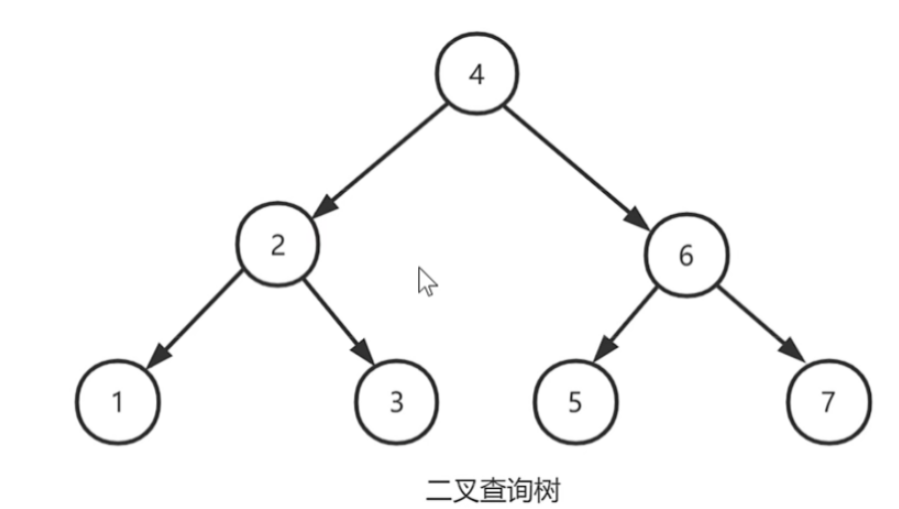
概述

二叉樹（Binary tree）是樹形結構的一個重要類型。許多實際問題抽象出來的數據結構往往是二叉樹形式，即使是一般的樹也能簡單地轉換為二叉樹，而且二叉樹的存儲結構及其算法都較為簡單，因此二叉樹顯得特別重要。二叉樹特點是每個節點最多只能有兩棵子樹，且有左右之分

特點

樹同時具有數組查詢的效率、鏈表增刪、改的性能

右子樹的結點比左子樹的節點大

查找法

搜索的數字如果比節點大則往右搜索，搜索的數字如果比節點小則往左搜索

結點實現原理

插入實現原理

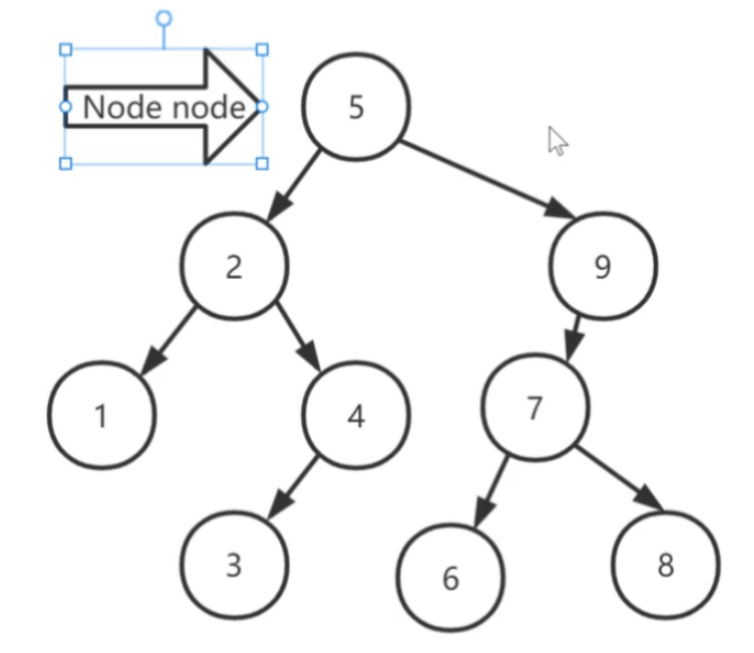
int[] arrs = {5,2,1,4,3,9,7,6,8};

如果樹是空樹，插入節點就直接放入到根結點

如果樹不是空樹，則插入的數字于根結點的數字進行比較

如果插入的值小于于結點的數字，則往左子樹插入

• 如果左子結點沒有元素就插入到左子結點中

• 如果左子結點有元素，就可以設計一個引用(游標)指向左子節點，并且再次和待插入的執行左子結點進行比較，直到找到插入的位置

如果插入的值大于結點的數字，則往右子樹插入

• 判斷右子結點是否存在值，如果不存在則直接插入

• 判斷右子結點是否存在值，如果存在則通過一個引用指向右子結點繼續和待插入的值進行比較，直到找到插入的位置

總結：

• 小往左，大往右

• 左子數永遠小于右子樹

遍歷實現原理

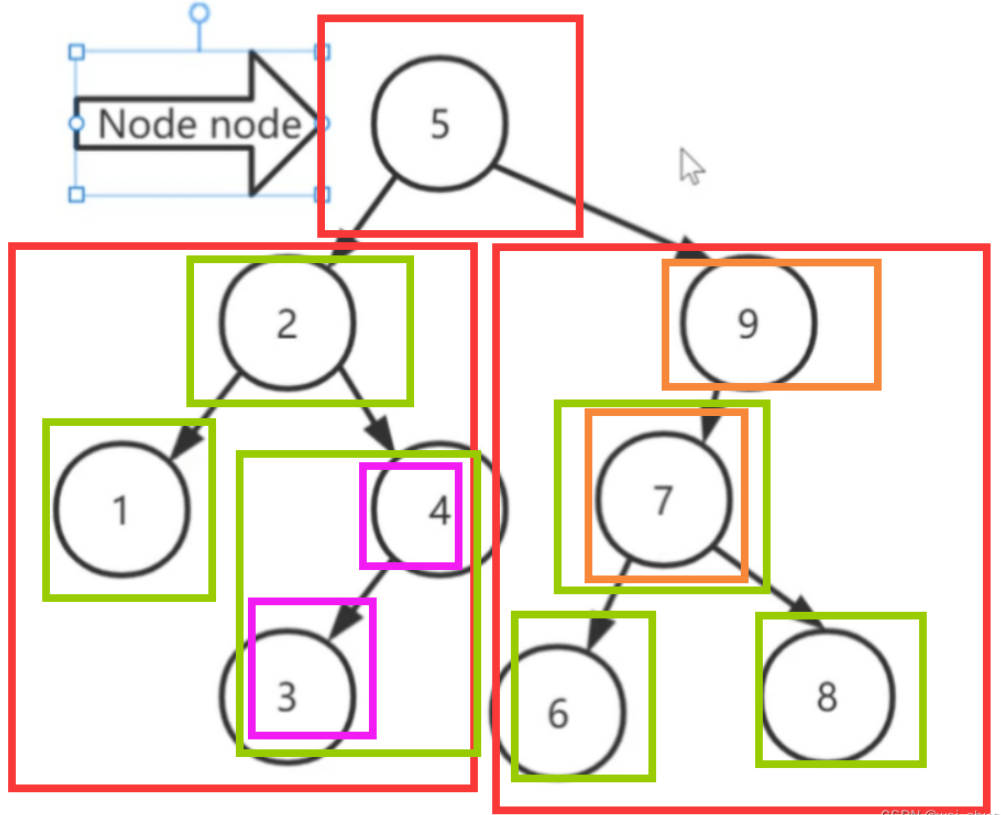
中序遍歷：左—根—右

通過中序遍歷就可以將二叉樹查找樹的進行順序輸出

總結：

始終貫徹左—根—右的原則、由內層向外層拆分

int[] arrs = {1,2,3,4,5,6,7,8,9};

刪除實現原理

提供一個待刪除的結點的值，根據值從二叉查找樹找到需要刪除的結點

找到待刪除結點的父類結點，并且要根據待刪除結點在父類結點的左右子樹的位置，設置為null進行刪除

需要考慮結點的三種情況

情況1：待刪除的結點沒有子結點

直接讓父類結點的對應目標結點引用設置為null即可

情況2：待刪除的結點有一個子節點

將待刪除的父類結點對應子節點的引用指向待刪除結點的子節點

情況3：待刪除的結點有兩個子節點 從左子樹中找到最大的結點進行刪除，并且將最大的結點的值放入到待刪除結點從右子樹中找到最小的結點進行刪除，并且將最小的結點的值放入(替換)到待刪除結點

(上述兩種刪除方法：需要將待刪除結點指向新創建(替換后的)的結點，并且將新的結點(替換后的)的左右結點指向待刪除的左右子樹的結點)

刪除的結點是根節點的情況

情況1：根節點沒有子節點，直接將根結點指向null

情況2：根結點有一個子節點，則根結點直接指向子節點

情況3：根結點有兩個子節點

可以從左子樹中找到最大值刪除結點，然后將最大值覆蓋(替換)根節點

可以從右子樹中找到最小值刪除結點，然后將最小值覆蓋(替換)根節點

結點插入與遍歷案例

BinarySearchTree類

package Algorithm;
public class BinarySearchTree {
    Node root;  //定義根節點
    //結點插入方法
    public void insert(int value) {
        if (root == null) {        //1.如果樹是空樹，插入節點就直接放入到根結點
            root = new Node(value);
        } else {     //如果樹不是空樹，則插入的數字于根結點的數字進行比較
            //2.如果插入的值小于于結點的數字，則往左子樹插入
            Node node = root;     //聲明一個游標結點，開始指向根節點
            while (true) {       //并且再次和待插入的執行左子結點進行比較，直到找到插入的位置
                if (value < node.value) {      //如果插入的值小于于結點的數字，則往左子樹插入
                    //2.1如果左子結點沒有元素就插入到左子結點中
                    if (node.left == null) {
                        node.left = new Node(value);
                        break;      //如果找到插入的位置，則跳出while循環
                    } else {         //如果左子結點有元素，就可以設計一個引用(游標)指向左子節點，并且再次和待插入的執行左子結點進行比較，直到找到插入的位置
                        //游標指向左子節點
                        node = node.left;
                    }
                } else {      //如果插入的值大于結點的數字，則往右子樹插入
                    //判斷右子結點是否存在值，如果不存在則直接插入
                    if (node.right == null) {
                        node.right = new Node(value);
                        break;
                    } else {     //判斷右子結點是否存在值，如果存在則通過一個引用指向右子結點繼續和待插入的值進行比較，直到找到插入的位置
                        //游標指向右子節點
                        node = node.right;
                    }
                }
            }
        }
    }
    //定義左右結點常量
    public static final int LEFT = 0; //左子節點
    public static final int RIGHT = 1; //右子節點
    //結點查找方法
    public void deleteNode(int value) {
        //定義游標從根節點開始查詢
        Node node = root;
        //定義目標結點
        Node target = null;
        //定義目標結點的父類結點
        Node parent = null;
        //目標結點的類型為，左子節點或者右子節點
        int nodeType = 0; //0代表左子節點 1代表右子節點

        while (node != null) { //游標不為空，如果為空則沒有子節點，無法刪除
            if (node.value == value) { //如果目標結點的值和需要刪除結點的值相同
                //找到結點
                target = node;
                break;
            } else if (value < node.value) {    //如果值不同，則判斷目標結點值是否小于node結點
                //保存父類結點
                parent = node;
                //游標指向左子節點
                node = node.left;
                nodeType = LEFT;
            } else { //如果值不同，且目標結點值大于node結點
                //保存父類結點
                parent = node;
                //游標指向右子節點
                node = node.right;
                nodeType = RIGHT;
            }
        }
        //如果沒找到需要刪除的目標結點
        if (target==null){
            System.out.println("沒有找到要刪除的結點");
            return;
        }
        //刪除結點的三種情況
        if (target.left == null && target.right == null) {   //情況1：待刪除的結點沒有子結點

            if (parent==null){      //刪除的結點沒有子結點
                //將root設置為null即可
                root=null;
                return;
            }
            //判斷目標的結點是左子節點還是右子節點
            if (nodeType == LEFT) {
                //將父類的左子節點設置為null
                parent.left = null;
            } else {
                //將父類的右子節點設置為null
                parent.right = null;
            }
        } else if (target.left != null && target.right != null) {   //情況2：待刪除的結點有2個子節點
            //兩個子節點，從target右子樹查找最小的值
            Node min=target.right;
            //遍歷左子樹
            while (min.left!=null){
                min = min.left;
            }
            //將最小的結點進行刪除
            deleteNode(min.value);
            //將待刪除的結點替換成最小的結點的值
            target.value= min.value;
        }else { //情況3：待刪除的結點有1個子節點
            //刪除結點是根節點
            if (parent==null){
                if (target.left!=null){ //判斷是左子節點還是右子節點有值
                    root=target.left;   //根節點=目標左子結點
                }else {
                    root=target.right;  //根節點=目標右子結點
                }
            }
            //只有一個子節點
            if (nodeType==LEFT){    //如果是左子節點
                if (target.left!=null){
                    //將父類的左子節點，指向待刪除結點的左子節點
                    parent.left=target.left;
                }else { //如果是右子節點
                    //將父類的左子節點，指向待刪除結點的右子節點
                    parent.left=target.right;
                }
            }else {
                if (target.right!=null){
                    //將父類的右子節點，指向待刪除結點的左子節點
                    parent.right=target.left;
                }else { //如果是右子節點
                    //將父類的右子節點，指向待刪除結點的右子節點
                    parent.right=target.right;
                }
            }
        }
    }
    //實現中序遍歷
    public void midTraversal(Node node) {
        if (node == null) {  //進行判斷結點不能為空，如果為空則退出
            return;
        } else {     //如果結點不為null，則執行下列遍歷語句
            //首先，遍歷左節點
            midTraversal(node.left);
            //打印根節點
            System.out.print(node.value + ",");
            //最后遍歷右子結點
            midTraversal(node.right);
        }
    }
    //創建一個結點類
    public static class Node {
        int value;  //存儲值
        Node left;  //左子樹
        Node right; //右子樹
        // 帶參構造方法，傳入value賦值
        public Node(int value) {
            this.value = value;
        }
    }
}

TestBST測試類

package Algorithm;
public class TestBST {
    public static void main(String[] args) {
        int[] arrs = {5, 2, 1, 4, 3, 9, 7, 6, 8};
        //創建二叉查詢樹
        BinarySearchTree tree = new BinarySearchTree();
        //將數組中的元素構造成二叉查詢樹
        for (int i = 0; i < arrs.length; i++) {
            tree.insert(arrs[i]);
        }
        //刪除結點
        tree.deleteNode(20);
        //中序遍歷根結點
        tree.midTraversal(tree.root);
    }
}

到此，關于“Java二叉樹查詢原理實例代碼分析”的學習就結束了，希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習，快去試試吧！若想繼續學習更多相關知識，請繼續關注億速云網站，小編會繼續努力為大家帶來更多實用的文章！