C語言平衡二叉樹問題怎么解決

這篇文章主要介紹“C語言平衡二叉樹問題怎么解決”的相關知識，小編通過實際案例向大家展示操作過程，操作方法簡單快捷，實用性強，希望這篇“C語言平衡二叉樹問題怎么解決”文章能幫助大家解決問題。

一、題目描述

給定一個二叉樹，判斷它是否是高度平衡的二叉樹。

本題中，一棵高度平衡二叉樹定義為：一個二叉樹 每個節點 的左右兩個子樹的高度差的絕對值不超過 1 。

二、解題思路

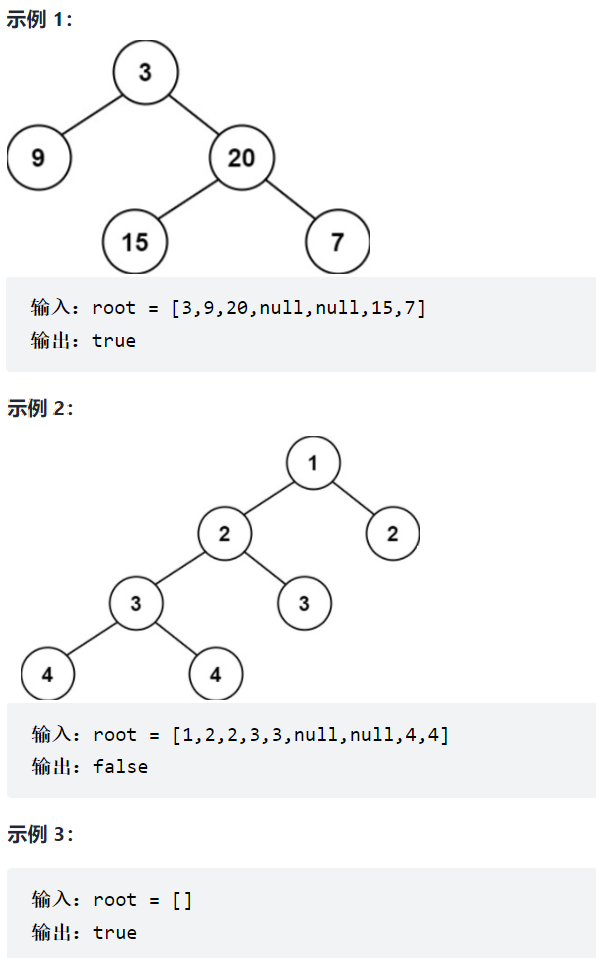
一棵二叉樹是平衡二叉樹，當且僅當其所有子樹也都是平衡二叉樹，因此我們使用遞歸的方式依次判斷其所有子樹是否為平衡二叉樹，就知道這棵二叉樹是不是平衡二叉樹了。

自頂向下的遞歸（暴力解法）

自頂向下類似于 前序遍歷，先判斷當前樹是否平衡，再判斷當前樹的左右子樹是否平衡。

核心思路

寫兩個函數：

子函數：計算當前任意一個節點(樹) root 的高度 root 是空節點：Depth ( root ) = 0root 是非空節點：Depth ( root ) = max ( Depth ( root->left ) , Depth ( root->right ) ) + 1

主函數：依次遞歸遍歷完 root 的所有子樹，對于「當前遍歷到的子樹」，判斷是否平衡，首先計算其左右子樹的高度，然后判斷高度差是否不超過 1

• 如果不超過，才能繼續往下遞歸遍歷「當前樹的左右子樹」，判斷其是否平衡；

• 如果超過1，說明不滿足平衡條件，則直接返回 false，不用往下遞歸了。

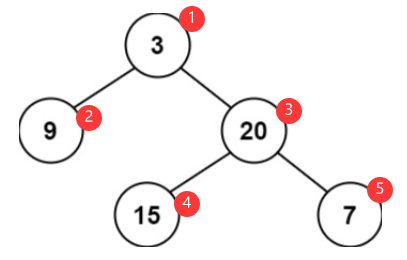
遞歸過程演示：自頂向下的遞歸類似于前序遍歷

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 計算當前任意一個節點(樹)的高度（子函數）
int TreeDepth(struct TreeNode* root)
{
    // 當前節點為空
    if(root == NULL)
    {
        return 0;
    }
    // 當前節點不為空，分別計算它的左右子樹的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 當前節點(樹)的高度
    return leftDepth > rightDepth ? leftDepth + 1 : rightDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 依次遞歸遍歷完root的所有子樹，分別判斷當前子樹是否為高度平衡二叉樹
    // 當前樹的根節點為空，說明其滿足高度平衡的二叉樹，返回true
    if(root == NULL)
    {
        return true;
    }
    // 當前樹的根節點不為空，分別計算它左右子樹的高度
    int leftDepth = TreeDepth(root->left);
    int rightDepth = TreeDepth(root->right);
    // 計算左右子樹的高度差
    int ret = leftDepth > rightDepth ? leftDepth - rightDepth : rightDepth - leftDepth;
    // 高度差不超過1，才能繼續往下遞歸遍歷當前樹的左右子樹
    return ret <= 1 && isBalanced(root->left) && isBalanced(root->right);
}

復雜度分析：

• 時間復雜度：O(n2)，其中 n 是二叉樹中的節點個數。

最壞情況下，二叉樹是滿二叉樹，主函數 isBalanced(root) 需要遍歷二叉樹中的所有節點，時間復雜度是 O(n)。計算每個子樹的最大高度函數 TreeDepth(root) 被重復調用。除了根節點，其余所有節點都會被遍歷兩次，復雜度為 O[2(n-1)]，所以時間復雜度為 n*2(n-1) ≈ n2。

• 空間復雜度：O(n)，其中 n 是二叉樹中的節點個數。空間復雜度主要取決于遞歸調用的層數，遞歸調用的層數不會超過 n。

自底向上的遞歸（最優解法）

方法一自頂向下遞歸，類似 前序遍歷，先判斷當前樹是否平衡，再判斷當前樹的左右子樹是否平衡，所以對于同一個節點，函數 TreeDepth 會被重復調用，會重復計算很多次子樹的高度，導致時間復雜度較高。

如果使用自底向上的做法，則對于每個節點，函數 TreeDepth 只會被調用一次。因為到達左子樹底部后，每次對應的左子樹都是放在遞歸調度中的，每次只需要獲取新的右子樹長度便可。

自底向上遞歸類似于 后序遍歷，對于當前遍歷到的節點，先遞歸地判斷其左右子樹是否平衡，再判斷以當前節點為根的子樹是否平衡。

• 如果當前樹的左/右子樹中只要有一個不平衡，則整個樹就不平衡，返回-1（表示不平衡）

• 如果當前樹是平衡的，則返回其高度，否則返回 -1（表示不平衡）。

寫遞歸算法需要關注什么？

• 整個遞歸的終止條件：遞歸應該在什么時候結束？— 子樹根節點為空的時候，空樹也是平衡二叉樹。

• 本級遞歸應該做什么？ — 判斷當前樹的左子樹、右子樹、以及當前樹是否是平衡的。

• 返回值：應該返回給上一級的返回值是什么？— 當前樹是平衡的，則返回其高度，不平衡則返回 -1。

遞歸算法流程：

每一級遞歸時，在我們眼中，當前樹就是這樣的，只有 root、left、right 三個節點。

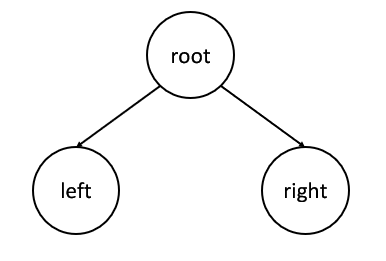
到葉子節點了，當前樹根節點 root 為空，說明是平衡的，則返回高度 0；

當前樹根節點 root 不為空，計算左右子樹 left 和 right 的高度，并判斷：

• 如果「左子樹 left 高度為 -1」、或「右子樹 right 高度為 -1」、或「左右子樹高度差 > 1」，說明整個樹 不平衡 ，直接返回 -1（表示不平衡）。

• 如果不滿足上面 3 種情況，說明當前樹是 平衡 的，返回當前樹的高度，即 max ( left, right ) + 1 。

補充：計算絕對值的函數：int abs( int n ); ，頭文件 <stdlib.h> or <math.h>。

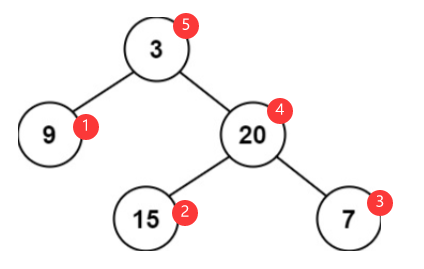
遞歸過程演示：自底向上遞歸類似于后序遍歷

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     struct TreeNode *left;
 *     struct TreeNode *right;
 * };
 */
// 計算當前樹的高度，并判斷當前樹是否是平衡二叉樹
int _isBalanced(struct TreeNode* root)
{
    // 先分別判斷當前樹的左/右子樹是否平衡
    // 如果當前樹的左/右子樹中只要有一個不平衡，則全樹就不平衡，返回-1（表示不平衡）
    // 如果當前樹的左右子樹都平衡，則繼續判斷當前樹是否平衡
    // 1. 到葉子節點了，當前樹根節點為空，說明是平衡的，則返回高度0
    if(root == NULL)
    {
        return 0;
    }
    // 2. 當前樹根節點不為空
    // 計算左右子樹的高度
    int leftTreeDepth = _isBalanced(root->left);
    int rightTreeDepth = _isBalanced(root->right);
    // 不平衡的3種情況：左子樹高度為-1，右子樹高度為-1，左右子樹高度差>1
    if(leftTreeDepth == -1 || rightTreeDepth == -1 || abs(leftTreeDepth - rightTreeDepth) > 1)
    {
        return -1;
    }
    // 如果不滿足上面3種情況，說明當前樹是平衡的，返回當前樹的高度
    return leftTreeDepth > rightTreeDepth ? leftTreeDepth + 1 : rightTreeDepth + 1;
}
bool isBalanced(struct TreeNode* root){
    // 遞歸遍歷過程中：
    // 只要有一個子樹高度為-1，說明整個樹是不平衡的，返回false
    // 所有子樹高度都不等于-1，說明整個樹是平衡的，返回true
    return _isBalanced(root) != -1;
}

復雜度分析：

1.時間復雜度：O(n)，其中 n 是二叉樹中的節點個數。

最壞情況是二叉樹為滿二叉樹時，需要遍歷完滿二叉樹中的所有節點，自底向上方法，因此每個節點只會被遍歷一次，所以時間復雜度是 O(n)。

2.空間復雜度：O(n)，其中 n 是二叉樹中的節點個數。空間復雜度卻決于遞歸調用的層數，有 n 個節點的二叉樹為單邊樹時深度最大，為 n。

關于“C語言平衡二叉樹問題怎么解決”的內容就介紹到這里了，感謝大家的閱讀。如果想了解更多行業相關的知識，可以關注億速云行業資訊頻道，小編每天都會為大家更新不同的知識點。