Java中堆的向下和向上調整示例分析

這篇文章主要介紹Java中堆的向下和向上調整示例分析，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

一、關于堆

JDK1.8中的PriortyQueue（優先級隊列）底層使用了堆的數據結構，而堆實際就是在完全二叉樹的基礎之上進行了一些元素的調整。

1.堆的概念

堆有最大堆和最小堆之分。
最大（最小）堆是一棵每一個節點的元素都不小于（大于）其孩子（如果存在）的元素的樹。大堆是一棵完全二叉樹，同時也是一棵最大樹。小堆是一棵完全二叉樹，同時也是一棵最小樹。
注意： 堆中的任一子樹也是堆，即大堆的子樹也都是大堆，小堆亦是。

2.堆的性質

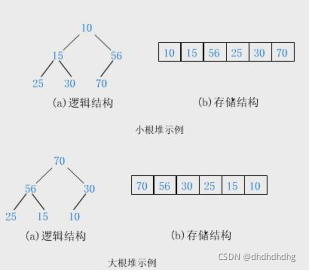
堆中某個結點的值總是不大于或不小于其父結點的值
堆總是一顆完全二叉樹

3.堆的存儲方式

由堆的概念可知，堆是一顆完全二叉樹，因此可以層序的規則采用順序的方式來高效存儲。
注意：對于非完全二叉樹，則不適合使用順序方式進行存儲，因為為了能夠還原二叉樹，空間中必須要能夠存儲空結點，就會導致空間利用率比較低

二、堆的創建

1.堆向下調整

對于給出的一個數據，如何將其創建為堆呢？例如下圖：

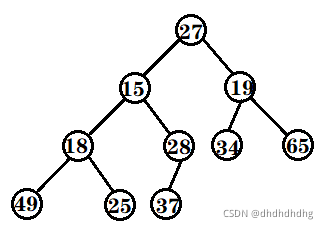
仔細觀察上圖后發現：根結點的左右子樹已經完全滿足堆的性質，因此只需將根結點向下調整好即可。
以小堆為例：

1.讓parent標記需要調整的結點，child標記parent的左孩子（注意：parent如果有孩子一定是先有左孩子）
2.如果parent的左孩子存在，即child<size，進行如下操作，直到parent的左孩子不存在

parent右孩子是否存在，如果存在則找出左右孩子中較小的孩子，使用child進行標記
將parent與較小的孩子（也就是此時的child）比較，如果：

parent小于較小的孩子child，這個結點已經調整
否則：將parent與child進行交換，交換成功后，這時parent中大的元素已經向下移動，可能會導致子樹不滿足堆的特性，就需要繼續向下調整，即parent=child,child=parent*2+1,然后循環起來

圖解如下：

代碼實現：

private void shiftDown(int parent){
        //默認讓child先標記左孩子---因為：parent可能有左沒有右
        int child=parent*2+1;

        //while循環條件可以保證：parent的左孩子一定存在
        //             但是不能保證parent的右孩子是否存在
        while(child<size){
            //1.找到左右孩子中較小的孩子
            if(child+1<size&&array[child+1]<array[child]){
                child+=1;
            }

            //2.較小的孩子已經找到了
            //檢測雙親和孩子之間是否滿足堆的特性
            if(array[parent]>array[child]){
                swap(parent,child);

                //大的雙親往下走，可能會導致子樹又不滿足堆的特性
                //因此需要繼續往下調整
                parent=child;
                child=parent*2+1;
            }else{
                //以parent為根的二叉樹已經是堆了
                return;
            }
        }
    }

注意： 在調整以parent為根的二叉樹時，必須要滿足parent的左子樹和右子樹已經是堆了才可以向下調整。
時間復雜度（看最壞的情況）： 從根一路比較到葉子，比較的次數為完全二叉樹的高度，即時間復雜度為O(logn)。

2.堆的創建

向下調整的情況只能針對左右子樹已經是堆了才可以調整，那假如根結點的左右子樹不滿足堆的特性，又該如何調整呢？例如下圖：

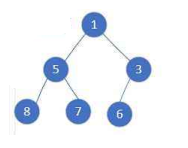
我們要從3這里的位置開始向下調整，然后逐漸向前依次向上調整
3這個位置很特殊，他是二叉樹倒數第一個非葉子結點
步驟：

1.找到倒數第一個非葉子結點
2.從該結點位置開始往前一直到根結點，每遇到一個結點就使用向下調整

代碼實現：

public static void createHeap(int[] array){
    //注意：倒數第一個非葉子節點剛好是最后一個節點的雙親
    //最后一個結點的編號是size-1，倒數第一個非葉子節點的下標為（size-1-1）/2
    int lastLeafParent=(size-2)/2;
    //從倒數第一個非葉子節點位置開始，一直到根節點的位置，使用向下調整
    for(int root=lastLeafParent;root>=0;root--){
       shiftDown(root);
    }
}

建堆的時間復雜度：
因為堆是完全二叉樹，滿二叉樹也是完全二叉樹，為了簡化計算，此處使用滿二叉樹來證明：
假設滿二叉樹高度h

第一層：20個結點，需要向下移動h-1層
第二層：21個結點，需要向下移動h-2層
第二層：22個結點，需要向下移動h-3層
…以此類推就可以求出所有的移動步數：每一層結點數與對應移動層數相乘再整體相加
然后再利用一定的數學巧妙運算（此處省略那些繁瑣的數學公式，屬實是頭大）就得出T(n)=n=log(n+1)≈n

因此：建堆的時間復雜度為O(N)。

三、向上調整

向上調整主要的應用場景就是在堆的插入
堆的插入總共需要兩個步驟：

1.先將元素插入到堆的末尾，即最后一個孩子之后
2.插入后如果堆的性質遭到破壞，將最后新插入的節點向上調整，直到滿足堆的性質

代碼實現：

private void shiftUp(int child){
        int parent=(child-1)/2;

        while(child!=0){
            if(array[child]<array[parent]){
                swap(child,parent);
                child=parent;
                parent=(child-1)/2;
            }else{
                return;
            }
        }
    }

以上是“Java中堆的向下和向上調整示例分析”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！