php中樹和二叉樹的定義及特點

本篇內容主要講解“php中樹和二叉樹的定義及特點”，感興趣的朋友不妨來看看。本文介紹的方法操作簡單快捷，實用性強。下面就讓小編來帶大家學習“php中樹和二叉樹的定義及特點”吧!

在計算機領域，我們天天要打交道的【文件夾】、數據庫中我們存儲的數據，都是樹的典型的應用。今天我們來學習的就是比較偏理論的關于樹和二叉樹的定義以及它們的一些屬性特點。

樹

從上面實際生活中的例子里，我們可以看出，樹這種結構是可以歸納出它的一些特點的。

樹 （Tree）是 N (N>0)個結點的有限集，它或為空樹（N=0）;或為非空樹 T 。

在這個定義中，我們需要明確兩個問題：一是樹一定是有結點的，二是根據結點數量可以分為空樹和非空樹兩種。不過這只是最基本的定義，它還有一些特性。

有且僅有一個稱之為根的結點。

也就是說，這個樹一定是從某一個結點開始擴展出來的，這個結點就向樹根一樣。從它開始向外開枝散葉。

除根結點以外的其余結點可分為 m ( m > 0 ) 個互不相交的有限集 T1，T2 ……，Tm 其中每一個集合本身又是一顆樹，并且稱為根的子樹（SubTree）

這一段可能會不太好理解，其實說白了就是每個結點只有一個上級結點，不能有多個上級結點。同理，平級結點之間也不能有聯系，但是它可以有多個下級結點。

關于樹的定義我們可以看下下面這個圖。

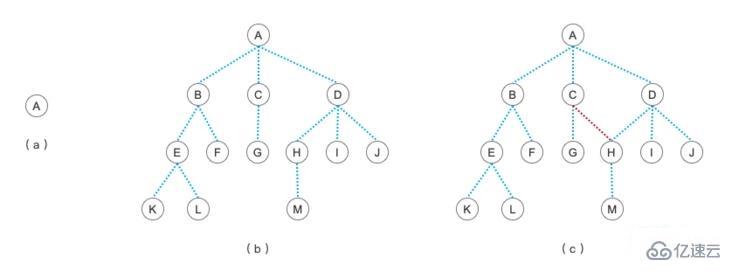
上圖中簡單的列舉了標準的樹和不標準的樹是什么樣子的。其中：

• (a) ，是只有一個根結點的樹，只要有一個結點，它就可以稱為一個樹結構

• (b) ，是一個標準的樹結構

• (c) ，注意它的 C 和 H 結點之間有一條連接線，這個就不是樹了，結點只能有一個上級結點的才稱為樹，這個其實就是我們將來要學的【圖】了

樹的相關術語

相對于棧的壓（入）棧、出棧，隊列的入隊、出隊來說，樹的相關術語可就復雜的多了。不論如何，首先你得先記住這些術語，要不后面講的東西用得那些術語只會讓你更暈。不過我們一時記不住也沒關系，先有個大概的印象，在后面的學習進程中遇到了再回來復習，這樣印象反而會更加深刻。

• 結點：一個結點可能包含一組數據，或者指向其它結點的分支，可以看作是樹枝分叉的那個地方，(b)圖中 A、 B、 C、 D、 E 等等這些都是結點

• 結點的度：結點擁有的子樹數量就叫做結點的度，其實就是它的下級子結點有幾個就是幾度，(b)圖中，C 結點的度為 1 ， D 結點的度為 3

• 樹的度：樹內各結點度的最大值，就是擁有最多子結點的度是多少，這個樹的度就是多少，(b) 圖這個樹的度為 3

• 葉子：度為0的結點，也就是沒有子結點的結點，(b) 圖中的 K 、 L 、 F 、 G 、 M 、 I 、 J 就是這顆樹的葉子結點

• 雙親和孩子：一個結點的子結點，就是它的孩子；對于這些子結點來說，當前這個結點就是它的雙親，(b) 圖中，D 的孩子是  H 、 I 、 J ，而  H 、 I 、 J 的雙親就是 D

• 層次：從根結點算起，根結點就是第一層，根的孩子就是第二層，依次類推，(b) 圖中 G 結點所在的層次為 3 ，(a) 圖的全部層次都只有 1

• 樹的深度（高度）：當前這顆樹的最大層次，很明顯，(b) 圖的深度就是 4

• 兄弟、祖先和子孫：兄弟結點就是這些結點的雙親是同一個結點；祖先結點就是從根結點到某個指定結點路上的經過的所有結點；子孫就是從某一個節點出發，到達目標結點這一路上的所有結點。(b) 圖中， E、 F 是兄弟，E 的祖先是 A 、 B ， E 的子孫為 K 或者 L

• 堂（表）兄弟：所有在同一層的結點但雙親不同的結點都是堂兄弟，同樣還是在 (b) 圖中，G 的堂（表）兄弟有  E、 F ，另外還有   H 、 I 、 J 也是它的表兄弟

二叉樹

對于樹的概念有了一定的了解之后，我們再來進一步的學習另一個概念，同時也是在數據結構和算法中最重要的一種樹的形式：二叉樹。

通常來說，樹的形態是可以千變萬化的，比如一個結點可以有 3 個子結點，而另一個結點可能有 300 個子結點。這樣沒有什么規則的樹其實操作起來會非常麻煩，而二叉樹的定義就要簡單的多，除了有樹的性質外，它還多了一項內容：二叉樹的每個結點最多只有兩個子結點，也就是說，整個二叉樹的度肯定是 2 ，所有結點的度也不會超過 2 。關于二叉樹為什么好操作這點，我們在下一小節的二叉樹的性質中再詳細地說明。所有的樹結構都是可以通過一定的規則變形來轉換成二叉樹的。

我們同樣還是通過一張圖示來展示什么是二叉樹。

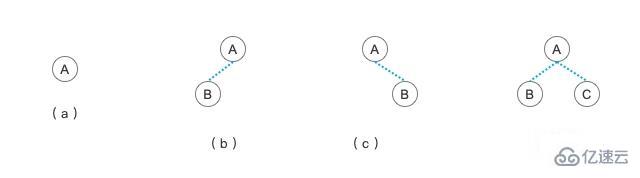
二叉樹中，左邊的子結點及其子孫結點可以看成是關于當前結點的左子樹。右邊結點及其子孫結點也一樣可以看成是當前結點的右子樹。根據結點的子結點情況，就有了上面圖中的這幾種二叉樹形態。

• (a) 樹是僅有一個結點的樹，也可以說是僅有一個結點的二叉樹

• (b) 樹是僅有一個左結點的二叉樹

• (c) 樹是僅有一個右結點的二叉樹

• (d) 樹是擁有左右兩個結點的二叉樹

二叉樹的性質

性質1：在二叉樹的第 i 層上至多有 2i-1 個結點（ i >= 1 ）

性質2：深度為 k 的二叉樹至多有 2k - 1 個結點（ k >= 1）

性質3：對任何一顆二叉樹 T ，如果其終端結點數為 n0 ，度為2的結點數為 n2 ，則 n0 = n2 + 1

性質4：具有 n 個結點 的完全二叉樹的深度為 log2n + 1

性質5：如果對一顆有 n 個結點 的完全二叉樹（其深度為 log2n + 1 ）的結點按層序編號（從第1層到第 log2n + 1 層，每層從左到右），則對任一結點 i （ 1 <= i <= n），有：

1. 如果 i = 1 ，則結點 i 是二叉樹的根，無雙親；如果 i > 1 ，則其雙親是結點 i / 2

2. 如果 2i > n ，則結點 i 無左孩子（結點 i 為葉子結點）；否則其左孩子是結點 2i

3. 如果 2i + 1 > n ，則結點 i 無右孩子；否則其右孩子是結點 2i + 1

關于二叉樹的上述五個性質的數學證明我們就不詳細說了，畢竟我們這一系列的文章的宗旨也是希望通過簡單的示例讓大家學習到數據結構和算法的精髓，而不是簡單粗暴的直接用數學公式來推導證明，那么我們就直接來圖上數一數就好了。

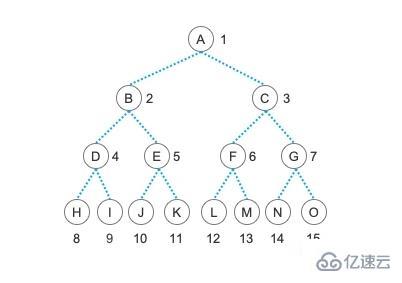
• 對于 性質1 來說，我們當前這個二叉樹根據公式的話，在第 3 層上最多只能有 23-1 個結點，也就是 4 個結點。第 4 層上最多只能有 24-1 ，也就是 23 = 8 個結點

• 對于 性質2 來說，當前這圖中的樹的深度為 4 ，也就是最多有 24 - 1 = 15 個結點

• 性質3 的話，我們先數數度為 2 的結點有多少，在這個圖中，度為 2 的結點有 7 個，也就是 A 、 B 、 C 、 D 、 E 、 F 、 G ，第 4 層的結點都是沒有子結點的，也就是說它們都是 0 度的，也稱為終端結點（葉子結點），這些結點的數量一共是 8 個。現在 n2 = 7 ，根據性質公式就可以得出 n0 = n2 + 1 = 7 + 1 = 8

• 圖中的結點數量為 15 個，套用 性質4 的公式可以得出 log2n + 1 = log215 + 1 = 3.91（向下取整） + 1 = 3 + 1 = 4 ，當前樹的深度即為 4 ，性質4 和 性質2 可以看作是互補的

• 對于 性質5 來說，請注意每個結點邊上的編號，我們就選取 E 結點來作為例子說明。E 結點當前為 5 ，所以它的雙親為 5 / 2 = 2 （向下取整）；E 的左孩子為 2i ，也就是 2*5=10 ，E 的右孩子為 2i + 1 ，也就是 2*5+1 = 11；性質5 的定義中說得更抽象一些，而且是拿葉子結點來做說明的，針對的是整個二叉樹的情況，但其實意思和我們這里解釋的是一樣的，大家可以再拿其它結點驗證一下。性質5 對于后面我們要講的使用順序結構來存儲二叉樹非常重要！

請務必掌握并記牢二叉樹的這五個性質及其含義，因為在后面的學習中，不管是二叉樹的順序、鏈式存儲結構，還是二叉樹的遍歷，都有可能會接觸到上面的五個性質中的內容。可以說，它們就是二叉樹學習中最最基礎的靈魂。

森林

最后，我們來簡單的了解下什么是“森林”。多個樹放在一起，就形成了一片“森林”。就像上文中二叉樹的解釋圖一樣，(a)(b)(c)(d)放在一起將它們整體一起來看，就是一片“森林”，在這片“森林”中分別有著(a)(b)(c)(d)這四顆樹。

森林中的樹和樹之間是沒有聯系的，如果我們要操作或者遍歷一個森林的話，往往是將這片森林轉化為一顆樹。具體的算法和步驟不是我們學習的重點，所以大家了解一下即可，有想深入研究的同學可以搜索相關的內容或者查閱相關的教材。

總結

從棧和隊列前進到樹后，是不是突然感覺到一下子就邁了一大步？有點搞不懂了？沒關系，今天的內容其實都是一些基礎的理論內容，能理解的就理解，不能理解的就接著繼續學習之后再返過來看今天的這些概念。

學習就不不斷地重復進步地過程，當然一切都還是要以地基為基礎的。當你了解了樹的數據結構及一些簡單的遍歷算法之后，再回來深入的理解這些概念并把他們背下來，相信一般的面試中關于樹相關的題目就不在話下了，一起努力吧！

到此，相信大家對“php中樹和二叉樹的定義及特點”有了更深的了解，不妨來實際操作一番吧！這里是億速云網站，更多相關內容可以進入相關頻道進行查詢，關注我們，繼續學習！