您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“Java排序算法的分類與介紹”,在日常操作中,相信很多人在Java排序算法的分類與介紹問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”Java排序算法的分類與介紹”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
排序是將一組數據,依指定的順序進行排列的過程
內部排序:指將需要處理的所有數據都加載到內部存儲器中進行排序.常見的內部排序有:直接插入排序、希爾排序、簡單選擇排序、堆排序、冒泡排序、快速排序、歸并排序、基數排序。
外部排序:數據量過大,無法全部加載到內存中,需要借助外部存儲進行排序。
度量一個程序(算法)執行時間的兩種方法:
事后統計方法這種方法可行,但是有兩個問題:一是要想對設計的算法的運行性能進行評測,需要實際運行該程序;二是所得時間的統計量依賴于計算機的硬件\軟件等環境因素,這種方式,要在同一臺計算機的相同狀態下運行,才能比較哪個算法速度更快.
事前估計方法通過分析算法的時間復雜度來判斷哪個算法更優.
一個算法花費的時間與算法中語句的執行次數成正比例,哪個算法中語句執行的次數多,它花費時間就多.一個算法中語句執行次數稱為語句頻度或時間頻度.記為T(n).
比如計算1-100所有數字之和,有兩種算法
int total=0; int end=100; //for循環計算 for(int i=1;i<=end;i++){ total+=i; }執行次數取決于end長度.它的T(n)=n+1.
//直接計算 total = (1+end)*end/2;
直接計算只需執行一次即可,它的T(n) = 1.
估算時間頻度時注意事項:
忽略常數項:如T(n)=2n+20和T(n)=2n,隨著n的變大,20可忽略.
忽略低次項:如T(n)=2n^2+3n+10和T(n)=2n^2,隨著n的變大,3n+10可以忽略.
忽略系數:如T(n)=5n^2+7n和T(n)=3n^2+2n,隨著n的變大,5和3可以忽略.
一般情況下,算法中的基本操作語句的重復執行次數是問題規模n的某個函數,用T(n)表示,若有某個輔助函數f(n),使得當n趨近于無窮大時,T(n)/f(n)的極限值為不等于零的常數,則稱f(n)是T(n)的同量級函數.記作T(n)=O(f(n)),稱O(f(n))為算法的漸進時間復雜度,簡稱時間復雜度.
T(n)不同,但是時間復雜度可能相同.如:T(n)=n^2+7n+6與T(n)=3n^2+2n+2,他們的T(n)不同,但是時間復雜度都是O(n^2)
計算時間復雜度方法
用常數1代替運行時間中的所有加法常數.
修改后的運行次數函數中,只保留最高階項.
去除最高階項的系數.
常數階O(1)
無論代碼執行了多少行,只要是沒有循環等復雜結構,那這個代碼的復雜度就是O(1)
int i = 1; int j = 2; ++i; j++; int m = i+j;
上述代碼在執行的時候,它消耗的時間并不是隨著某個變量的增長而增長,那么無論這類代碼有多長,即使有幾萬幾十萬行,都可以用O(1)來表示它的時間復雜度.
對數階O(log2n)
int i = 1; while(i<n){ i = i*2; }在while循環里面,每次都將i乘以2,乘完之后,i距離n就越來越近了.假設循環x次之后,i就大于n了,此時循環就結束了,也就是說2的x次方等于n,那么x= log2n也就是說當循環log2n次以后,這個代碼就結束了.因此這個時間復雜度為O(log2n).
線性階O(n)
for(i=1;i<=n;i++){ j = i; j++; }for循環里面的代碼會執行n遍,因此它消耗的時間是隨著n的變化而變化的,因此這類代碼都可以使用O(n)來表示它的時間復雜度.
線性對數階O(nlog2n)
for(int m=1;m<n;m++){ i = 1; while(i<n){ i = i*2; } }這個線性對數階O(log2n)就是將時間復雜度為O(logn)的代碼循環N遍.
平方階O(n^2)
即雙層for循環,n*m
立方階O(n^3)
3層循環
K次方階O(n^k)
k次循環
指數階O(2^n)
常見的算法時間復雜度由小到大依次為:O(1)
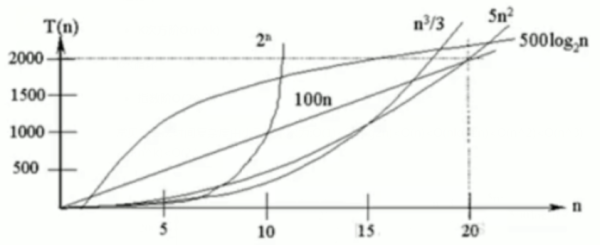
平均時間復雜度是指所有可能的輸入實例均以等概率出現的情況下,該算法的運行時間.
最壞情況下的復雜度稱最壞時間復雜度.一般討論的時間復雜度是最壞情況下的時間復雜度.這樣做的原因是:最壞情況下的時間復雜度是算法在任何輸入實例上運行時間的界限,這就保證了算法的運行時間不會比最壞情況更長.
平均時間復雜度和最壞時間復雜度是否一致,和算法有關(如下表).

類似于時間復雜度的討論,一個算法的空間復雜度(Space complexity)定義為該算法所耗費的存儲空間,它也是問題規模n的函數.
空間復雜度是對一個算法在運行過程中臨時占用存儲空間大小的度量.有的算法需要占用的臨時工作單元數與解決問題的規模n有關,它隨著n的增大而增大,當n較大時,將占用較多的存儲單元,例如快速排序和歸并排序就屬于這種情況.
在做算法分析時,主要討論的時間復雜度.從用戶體驗上看,更看重程序執行的速度.一些緩存產品(Redis,Memcache)和算法(基數排序)本質就是用空間換時間.
到此,關于“Java排序算法的分類與介紹”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。