用Python解釋SpaceX怎么進行火箭回收

這篇文章主要為大家展示了“用Python解釋SpaceX怎么進行火箭回收”，內容簡而易懂，條理清晰，希望能夠幫助大家解決疑惑，下面讓小編帶領大家一起研究并學習一下“用Python解釋SpaceX怎么進行火箭回收”這篇文章吧。

為了進一步了解非線性控制，我一直在嘗試一種非常有效的方法，稱為軌跡優化。設置完基本代碼后，就可以很容易地將其應用于各種系統。

在看完Starship SN15發射后，我決定進行一些動力學估算，以檢驗我的2D模擬玩具是否能執行翻轉并自行著陸。令我興奮的是，經過一番細心的研究，它運行得很好。但是真正令我驚訝的是當我與實際的著陸畫面并排播放輸出時：它的軌跡非常完美。而且編寫整個程序和優化時我并沒有參考視頻或其他明確的計時信息。

對我而言有兩種可能：1、我非常幸運，2、SpaceX在其實際系統上運行了非常相似的優化。這是一個非常有趣的東西，希望能為進入火箭回收后面的魔法打開一扇窗戶。在開始編寫代碼之前，可能最好先解釋一下軌跡優化的理論（但如果您愿意，也可以直接跳轉至代碼）。

軌跡優化：“最優軌跡”意味著什么？

在這種情況下，“最佳”表示通常的含義：“好”，“最佳”，“理想”等。舉一個簡單的例子，假設您想走過整個房間到達冰箱：您可以選擇看似無數的路線，但是以某種方式只能選擇其中一條路線。

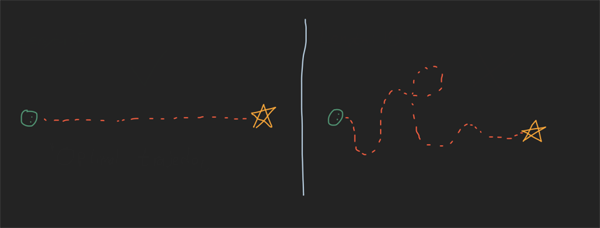
兩條軌跡的例子

應該很容易看到有好路線和差路線，但是實際上定義好軌跡還是差軌跡的是什么呢？這就是“成本”概念進入的地方。如果您有機器學習的經驗，那么這基本上是相同的概念。您運行優化以最小化成本函數。在我們的冰箱示例中，成本函數是什么？一個簡單的方法就是走我們的路。現在可以要求計算機在您和冰箱之間找到一條長度最短的路徑。

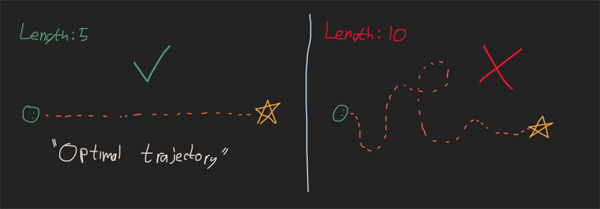
選擇成本函數

這可行，但有一些細微的缺陷。想象一下，您和冰箱之間有一個死亡陷阱。我們的“查找最小長度”算法將使您正確地進行操作，我認為您可能會認為這并不是真正的最佳選擇。

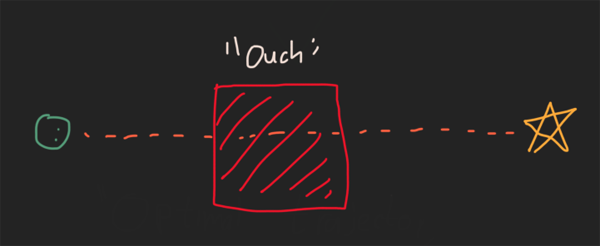
可能更好的成本函數（以及我在Starship著陸代碼中主要使用的函數）基于“努力”。假設您在地板上向前邁出一步需要您付出1點努力，而經過死亡之坑™則需要您花費1000點努力。這更好地匹配了我們認為是最佳與非最佳的條件：

約束

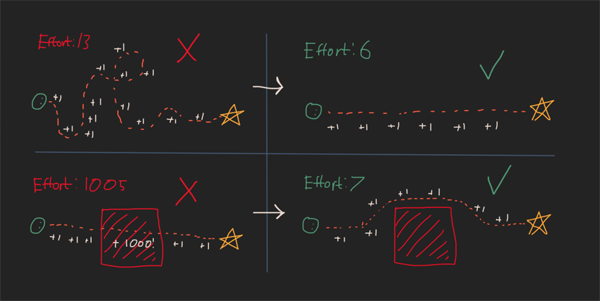
很少有優化問題可以在沒有很多約束的情況下完成，這是一些“邏輯”問題，可以解決我們的冰箱問題。

其他資料

這是軌跡優化的核心。通過最小化某些成本函數并保持一組約束來優化點之間的軌跡。這里有一些很好的資源，它們在數學方面會更深入：

https://www.youtube.com/watch?v=wlkRYMVUZTs

為火箭著陸進行編碼！

現在到有趣的東西上。有一些很棒的庫可以遍歷方程式并進行優化工作，因此真正的“藝術”在于向解釋器提出正確的問題。下面是一個指向collab notebook的鏈接，可讓您在瀏覽器中運行全部代碼：

https://colab.research.google.com/drive/18MVtu4reVJLBE1RXByQEmu0O9aLXlMHz?usp=sharing

軌跡

時間被切成0.04s的塊，并在每個步驟中生成了火箭狀態和控制狀態的變量。這導致沿路徑產生一堆離散點，這些點比較容易處理，然后嘗試為整個對象提出封閉形式的解決方案。

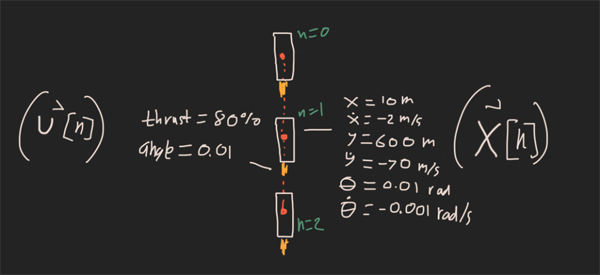
由三個點和沿著該軌跡的狀態組成的軌跡的示例

火箭狀態向量：x[n] = [x, x_dot, y, y_dot, theta, theta_dot]

控制狀態向量：u[n] = [thrust_mag, thrust_angle]

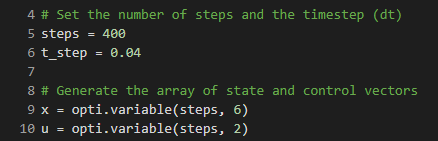
生成步驟和優化變量

之所以選擇0.04s是因為它可以以每秒25幀的速度進行1：1播放。是的，實際上我確實更改了仿真時間步長，因為25 fps看起來不錯。

為了找到時間步長，我手動增加了時間步長，直到找到可行的解決方案為止。有多種方法可以讓求解器自行發現最短的時間軌跡（主要是：讓它確定點之間的時間步長）。

成本函數

設置成本函數

所有成本都是平方和-> cost [0]²+ cost [1]²+ cost [2]²…依此類推。

最小化推力輸出——理想情況下，您希望在著陸時使用少量燃油。

最小化TVC的萬向節角度——移動噴嘴很費力，理想情況下，您希望它名義上指向下方。

最小化角速度——似乎有點荒唐，但我有一種直覺，即角速度/加速度會在發動機上施加最大的應變，因此您希望將其保持在盡可能低的水平。

約束集1：初始條件和最終條件

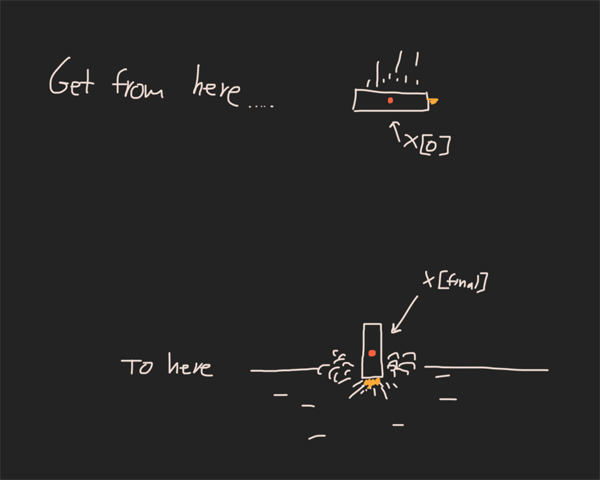
初始條件是在空氣中以90m / s的速度向下旋轉90度然后開始向下飛行1000m。

初始條件和最終條件約束

起始高度和速度來自飛行俱樂部的SN9數據：https：//flightclub.io/result/2d？code = SN91

約束集2：動態

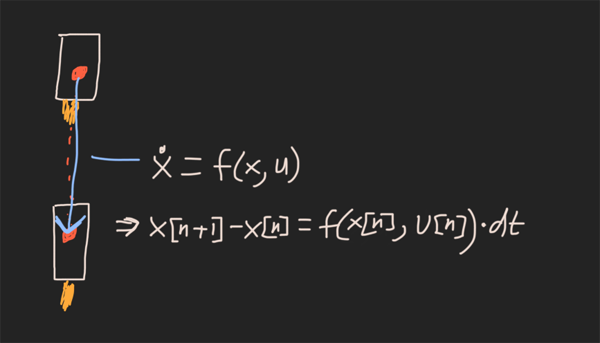
每個狀態時間步都必須服從：x [n + 1] -x [n] = f（x [n]，u [n]）* dt

本質上，這是“不要破壞物理”的約束。它等效于火箭的離散時間模擬，下一個狀態等于當前狀態+導數* dt。（注意：我在代碼中使用x_dot（）而不是f（），因為我認為它更易于閱讀）。

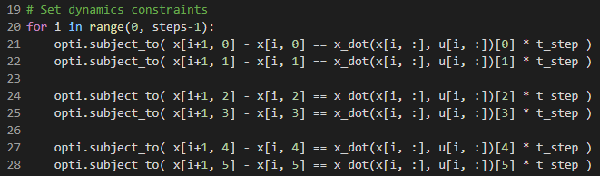
為狀態向量中的所有元素設置動力學約束

飛行常數和動力學功能：

g = 9.8

m = 100000公斤（猜測濕重和干重之間的一個很好的舍入數。實際上，當您使用燃料時，這種情況會發生變化，但出于準確性考慮，我只是為了簡單起見）

長度= 50米

I =（1/12）* m *長度²（均勻桿的慣性）

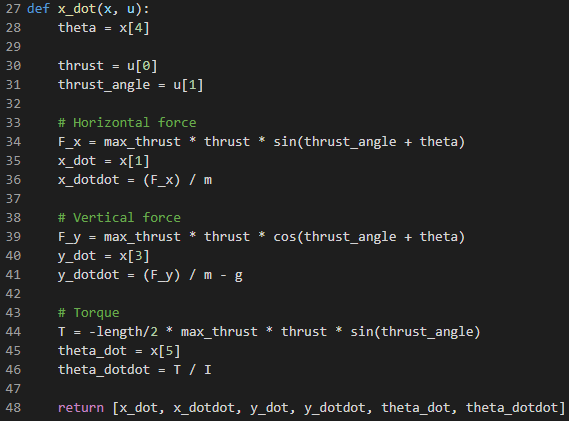
定義f（x，u）= x_dot

（注意：這是一個相當差的離散化，并且存在更好的方法，例如并置。但是，這是寫出來的最簡單，最快的方法）

約束集3：可變范圍

推力不能超過一個猛禽戰機的最大值，油門不能低于40％，推力矢量控制在每個方向上的擺角都不能超過20度 Raptor max取自維基百科，+-20度完全是個猜測，我很想知道是否有更可靠的數據用于此。

設置u的有界約束

優化！

剩下要做的就是運行它！

選擇求解器并運行！

基本上就是這樣，您調用opti.solve（），然后將其轉換為Ipopt（開放源代碼優化求解器）可以理解的問題。希望此消息應該到達大量迭代打印的底部：

這就是我們想要看到的

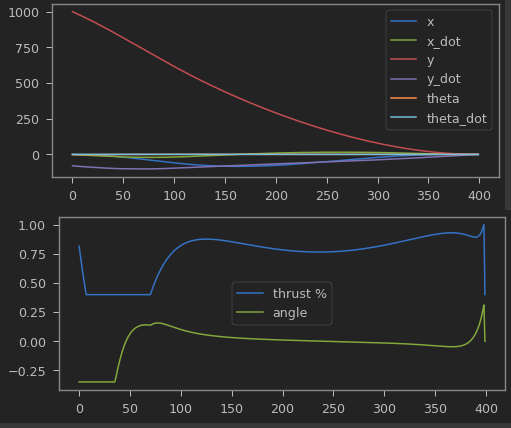
狀態和控制陣列圖

下一部分代碼使用matplotlib制作了漂亮的動畫，需要花一點時間來生成所有幀，但結果還是很不錯的。

總結

雖然接近完美的軌道可能主要是讓我對事物的估計感到幸運，但仍有一些有趣的東西可以借鑒，主要是：

Starship很有可能要么遵循預先計劃的優化軌跡，要么運行實時優化以動態生成最優軌跡。（或兩者混合）

不僅如此，我們可以進一步猜測它們的優化成本函數/“目標”與我們的非常相似：最小化推力，最小化TVC角和最小化角速度。這條賽道有時幾乎是不可思議的，尤其是在雙向滑行的情況下。（我一直以為這是過沖，但這可能只是到達著陸點的最佳路徑）。這也是一個有趣的分析工具，我真的很想找出導致SN8和SN9著陸失敗的一些其他約束（需要進行一些調整：最終狀態不再是嚴格的約束）。

為什么實際上著陸火箭比這要難得多

“哇，我剛剛想出了SpaceX是如何著陸他們的火箭的！！”，但可悲的是，事實并非如此。

一旦生成了一條物理上可能的軌跡，該軌跡將您帶到了您想去的地方，那么您需要做的很多事情才能真正沿著該軌跡運動：狀態估計，閉環反饋控制，基于實際運動軌跡的動態更新時間條件……還有很多真正的航空工程師知道的東西。除此之外，這些求解器還需要花費很長時間才能運行，并且在線（實時）優化很難正確而安全地完成：一個錯誤的輸入，您的求解器可能會發出“失敗”的聲音，從而導致故障發生。

以上是“用Python解釋SpaceX怎么進行火箭回收”這篇文章的所有內容，感謝各位的閱讀！相信大家都有了一定的了解，希望分享的內容對大家有所幫助，如果還想學習更多知識，歡迎關注億速云行業資訊頻道！