您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹了python怎么用蒙特·卡羅方法求圓周率的相關知識,內容詳細易懂,操作簡單快捷,具有一定借鑒價值,相信大家閱讀完這篇python怎么用蒙特·卡羅方法求圓周率文章都會有所收獲,下面我們一起來看看吧。
蒙特·卡羅方法求圓周率
介紹:
蒙特·卡羅方法(Monte Carlo method),也稱統計模擬方法,是二十世紀四十年代中期由于科學技術的發展和電子計算機的發明,而被提出的一種以概率統計理論為指導的一類非常重要的數值計算方法。是指使用隨機數(或更常見的偽隨機數)來解決很多計算問題的方法。與它對應的是確定性算法。蒙特·卡羅方法在金融工程學,宏觀經濟學,計算物理學(如粒子輸運計算、量子熱力學計算、空氣動力學計算)等領域應用廣泛。
其實,高中數學里的幾何概型(P=陰影部分面積(或區間或體積)/總面積(或區間或體積))就是一種蒙特·卡羅方法。
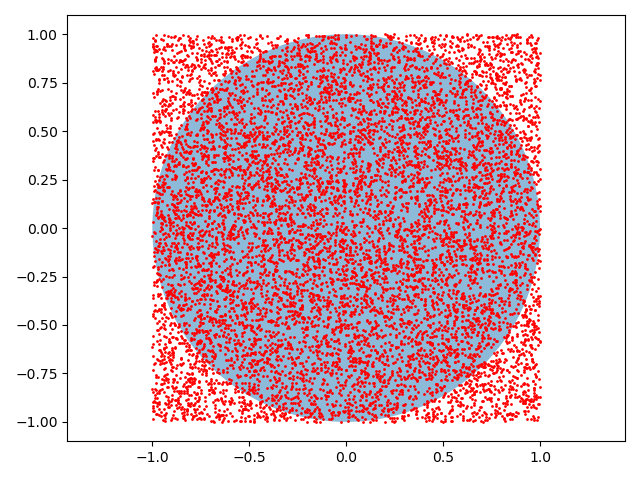
import numpy as npimport matplotlib.pyplot as pltfrom matplotlib.patches import Circle# 投點次數n = 10000# 圓的信息r = 1.0 # 半徑a, b = (0., 0.) # 圓心# 正方形區域邊界x_min, x_max = a-r, a+ry_min, y_max = b-r, b+r# 在正方形區域內隨機投點x = np.random.uniform(x_min, x_max, n) # 均勻分布y = np.random.uniform(y_min, y_max, n)# 計算 點到圓心的距離d = np.sqrt((x-a)**2 + (y-b)**2)# 統計 落在圓內的點的數目res = sum(np.where(d < r, 1, 0))# 計算 pi 的近似值(Monte Carlo方法的精髓:用統計值去近似真實值)pi = 4 * res / nprint('pi: ', pi)spi = 3.1415926535print('這里近似的圓周率與10位的圓周率精確度是: ', (spi - pi)/spi )# 畫個圖看看fig = plt.figure()axes = fig.add_subplot(111)axes.plot(x, y,'ro',markersize = 1)plt.axis('equal') # 防止圖像變形circle = Circle(xy=(a,b), radius=r, alpha=0.5)axes.add_patch(circle)plt.show()
執行結果:
pi: 3.1224這里近似的圓周率與10位的圓周率精確度是: 0.006109211351324613
關于“python怎么用蒙特·卡羅方法求圓周率”這篇文章的內容就介紹到這里,感謝各位的閱讀!相信大家對“python怎么用蒙特·卡羅方法求圓周率”知識都有一定的了解,大家如果還想學習更多知識,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。