1  引言

先舉個例子：

#include <stdio.h>

int main()
{
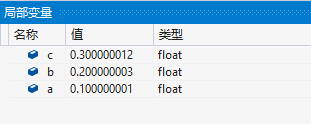
   float a = 0.1;
   float b = 0.2;
   float c = a + b;

   if(c == 0.3){
      printf("c == 0.3\n");
   }else{
      printf("0.1 + 0.2  != 0.3\n");
   }
   return 0;
} 

 

 

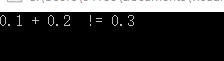
如果變量 a , b 換 0.75 ， 0.5 可以看出運行出 c == 1.25 ,說明浮點數運算是不穩定的。

 

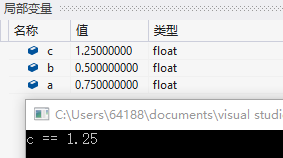
為什么會時好時壞，因為不是所有的小數能用浮點數標準 ( IEEE 754 ) 表示出來。

所以，判斷兩個浮點數變量是否相等，不能簡單地通過  "=="  運算符實現，浮點數進行比較時，一般比較他們之間的差值在一定范圍之內。

bool feq(float a,float b){
 return fabs(a,b)<FLT_EPSILON;
} 

FLT_EPSILON 數值是 1.192092896e-07F,最小的  float  型數，它使 1.0+FLT_EPSILON !=1.0 

2  為什么浮點數精度會丟失

十進制小數轉化為二進制數：乘以2直到沒有了小數為止。

舉個例子，0.9 表示成二進制數。

   0.9*2=1.8   取整數部分 1
   0.8(1.8的小數部分)*2=1.6    取整數部分 1
   0.6*2=1.2   取整數部分 1
   0.2*2=0.4   取整數部分 0
   0.4*2=0.8   取整數部分 0
   0.8*2=1.6   取整數部分 1
   0.6*2=1.2   取整數部分 0
    .........     
   0.9二進制表示為(從上往下): 1100100100100...... 

很顯然，小數的二進制表示有時是不可能精確的。其實道理很簡單，十進制系統中能不能準確表示出  2/3  呢？同樣二進制系統也無法準確表示  1/10  。這也就解釋了為什么浮點型精度丟失問題。

3  float 存儲原理

float  型在內存中占  4  個字節。float  的  32  個二進制位結構如下：

float  內存存儲結構

其中符號位 1 表示正，0  表示負。有效位數位 24 位，其中一位是實數符號位。

將一個 float 型轉化為內存存儲格式的步驟為：

• 先將這個實數的絕對值化為二進制格式，注意實數的整數部分和小數部分的二進制方法在上面已經探討過了。
• 將這個二進制格式實數的小數點左移或右移 n 位，直到小數點移動到第一個有效數字的右邊。
• 從小數點右邊第一位開始數出二十三位數字放入第 22 到第 0 位。
• 如果實數是正的，則在第 31 位放入“0”，否則放入“1”。
• 如果  是左移得到的，說明指數是正的，第 30 位放入“1”。如果 n 是右移得到的或 n=0，則第 30 位放入“0”。
• 如果 n 是左移得到的，則將 n 減去 1 后化為二進制，并在左邊加“0”補足七位，放入第 29 到第 23 位。如果n是右移得到的或 n=0，則將 n 化為二進制后在左邊加“0”補足七位，再各位求反，再放入第 29 到第 23 位。

0.2356 的內存存儲格式：

• 將 0.2356 化為二進制后大約是0.00111100010100000100100000。
• 將小數點右移三位得到1.11100010100000100100000。
• 從小數點右邊數出二十三位有效數字，即11100010100000100100000放 入第 22 到第 0 位。
• 由于 0.2356 是正的，所以在第 31 位放入“0”。
• 由于我們把小數點右移了，所以在第 30 位放入“0”。
• 因為小數點被右移了 3 位，所以將 3 化為二進制，在左邊補“0”補足七位，得到0000011，各位取反，得到1111100，放入第 29 到第 23 位。
• 最后表示0.2356為：0 0 1111100 11100010100000100100000 

浮點類型標識的有效數字及數值范圍

• Float ：比特數為 32 ，有效數字為 6-7 ，數值范圍為     -3.4E+38～3.4E+38
• Double ：比特數為 64 ，有效數字為 15-16 ，數值范圍為     -1.7E-308～1.7E+308