您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
這篇文章主要介紹“C++如何實現線段樹”,在日常操作中,相信很多人在C++如何實現線段樹問題上存在疑惑,小編查閱了各式資料,整理出簡單好用的操作方法,希望對大家解答”C++如何實現線段樹”的疑惑有所幫助!接下來,請跟著小編一起來學習吧!
假設有這樣的問題:有n個數,m次操作,操作分為:修改某一個數或者查詢一段區間的值
分析下,如果針對數組元素的修改可以是O(1)完成,求某個區間值需要O(n)才可以完成,如果m和n都很大的情況,這個復雜度就很難接受了。
我們之前學過的前綴和算法可以解決區間求和的問題,并且時間復雜度是O(1),但如果涉及到修改操作,前綴和數組都需要重新計算,時間復雜度也是O(n)
有沒有什么辦法可以兼顧以上兩種操作,并且可以將時間復雜度降低?
這就是我們要學習的線段樹!把修改和查詢的時間復雜度都降到O(logn)!!!
先來看下線段樹長什么樣:
有以下數組(為方便計算,數組下標從1開始)
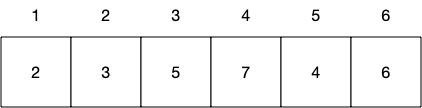
我們把它轉換成線段樹,是長這樣的:
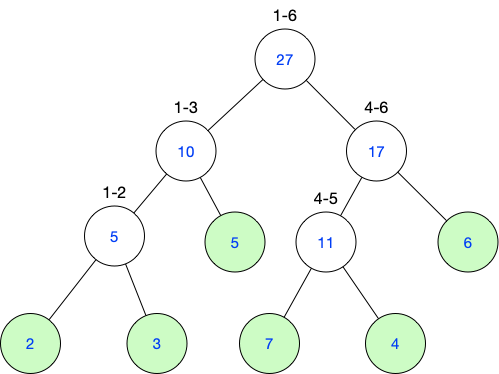
1)葉子結點(綠色)存的都是原數組元素的值
2)每個父結點是它的兩個子節點的值的和
3)每個父結點記錄它表示區間的范圍,如上圖的“1-2”表示1到2的區間
下面我們來看看線段樹是如何降低操作復雜度的!
例如我們需要查詢2-5區間的和
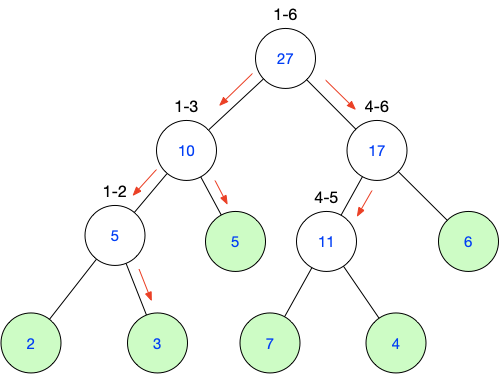
使用遞歸的思想:
2~5的和
=2~3的和+4~5的和
=3+5+4~5的和
=3+5+11
=19
總之,就是沿著線段樹的劃分把區間分開,再加到一塊就行啦!
例如,我們要把結點2的值由3->5,線段樹需要沿著紅色部分一個一個改,直到根結點:
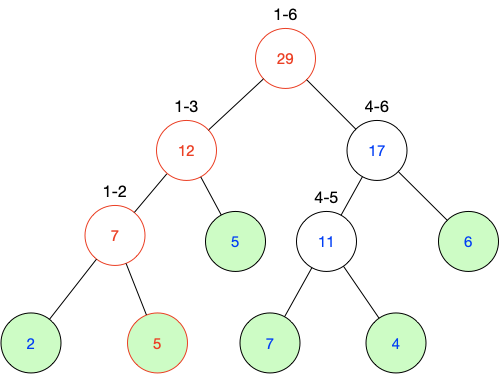
不管是修改操作還是查詢操作,時間復雜度都是O(logn)
下一步我們來看怎么實現線段樹!
首先我們需要將原始數組建立成一顆線段樹,然后在樹的基礎上提供查詢和修改的操作。
觀察上圖,我們發現線段樹是一棵近似完全二叉樹,利用完全二叉樹的性質,我們就可以直接用一個數組來存它。
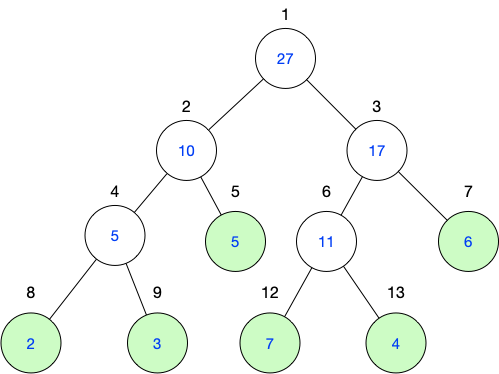
就像上圖一樣把各個節點標上號,如果根節點編號是n,那它的左子樹編號是2n,右子樹的編號是2n+1
所以說,知道了根節點的編號,我們就可以快速有效的找到左右子樹的根節點
void build(int root,int start,int end){
if(start == end){
tree[root] = num[start];
return;
}
int leftroot = root * 2;//左結點
int rightroot = root * 2 + 1;//右結點
int mid = (start+end)/2;
build(leftroot,start,mid);//遞歸計算左結點
build(rightroot,mid+1,end);//遞歸計算右結點
tree[root] = tree[leftroot] + tree[rightroot];//根結點值=左根+右根
}int query(int root,int start,int end,int l,int r){
if(l<=start && r>= end){
return tree[root];
}
int leftroot = root * 2;
int rightroot = root * 2 + 1;
int mid = (start+end)/2;
int sum = 0;
if(l<=mid){
sum += query(leftroot,start,mid,l,r);
}
if(r>mid){
sum += query(rightroot,mid+1,end,l,r);
}
return sum;
}/**
* 修改[l,r]區間里的數,都加上k值
* @param root
* @param start
* @param end
* @param l
* @param r
* @param k
*/
void update(int root,int start,int end,int l,int r,int k){
if(start == end){
tree[root] += k;
return;
}
int leftroot = root * 2;
int rightroot = root * 2 + 1;
int mid = (start+end)/2;
if(l<=mid){
update(leftroot,start,mid,l,r,k);
}
if(r>mid){
update(rightroot,mid+1,end,l,r,k);
}
tree[root] = tree[leftroot] + tree[rightroot];
}到此,關于“C++如何實現線段樹”的學習就結束了,希望能夠解決大家的疑惑。理論與實踐的搭配能更好的幫助大家學習,快去試試吧!若想繼續學習更多相關知識,請繼續關注億速云網站,小編會繼續努力為大家帶來更多實用的文章!
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。