您好,登錄后才能下訂單哦!
您好,登錄后才能下訂單哦!
簡介
CART與C4.5類似,是決策樹算法的一種。此外,常見的決策樹算法還有ID3,這三者的不同之處在于特征的劃分:
ID3:特征劃分基于信息增益
C4.5:特征劃分基于信息增益比
CART:特征劃分基于基尼指數
基本思想
CART假設決策樹是二叉樹,內部結點特征的取值為“是”和“否”,左分支是取值為“是”的分支,右分支是取值為“否”的分支。這樣的決策樹等價于遞歸地二分每個特征,將輸入空間即特征空間劃分為有限個單元,并在這些單元上確定預測的概率分布,也就是在輸入給定的條件下輸出的條件概率分布。
CART算法由以下兩步組成:
決策樹生成:基于訓練數據集生成決策樹,生成的決策樹要盡量大;
決策樹剪枝:用驗證數據集對已生成的樹進行剪枝并選擇最優子樹,這時損失函數最小作為剪枝的標準。
CART決策樹的生成就是遞歸地構建二叉決策樹的過程。CART決策樹既可以用于分類也可以用于回歸。本文我們僅討論用于分類的CART。對分類樹而言,CART用Gini系數最小化準則來進行特征選擇,生成二叉樹。 CART生成算法如下:
輸入:訓練數據集D,停止計算的條件:
輸出:CART決策樹。
根據訓練數據集,從根結點開始,遞歸地對每個結點進行以下操作,構建二叉決策樹:
設結點的訓練數據集為D,計算現有特征對該數據集的Gini系數。此時,對每一個特征A,對其可能取的每個值a,根據樣本點對A=a的測試為“是”或 “否”將D分割成D1和D2兩部分,計算A=a時的Gini系數。
在所有可能的特征A以及它們所有可能的切分點a中,選擇Gini系數最小的特征及其對應的切分點作為最優特征與最優切分點。依最優特征與最優切分點,從現結點生成兩個子結點,將訓練數據集依特征分配到兩個子結點中去。
對兩個子結點遞歸地調用步驟l~2,直至滿足停止條件。
生成CART決策樹。
算法停止計算的條件是結點中的樣本個數小于預定閾值,或樣本集的Gini系數小于預定閾值(樣本基本屬于同一類),或者沒有更多特征。
代碼
代碼已在github上實現(調用sklearn),這里也貼出來
測試數據集為MNIST數據集,獲取地址為train.csv
運行結果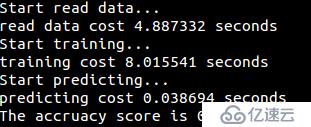
為了幫助大家讓學習變得輕松、高效,給大家免費分享一大批資料,幫助大家在成為大數據工程師,乃至架構師的路上披荊斬棘。在這里給大家推薦一個大數據學習交流圈:658558542 歡迎大家進×××流討論,學習交流,共同進步。
當真正開始學習的時候難免不知道從哪入手,導致效率低下影響繼續學習的信心。
但最重要的是不知道哪些技術需要重點掌握,學習時頻繁踩坑,最終浪費大量時間,所以有有效資源還是很有必要的。
最后祝福所有遇到瓶疾且不知道怎么辦的大數據程序員們,祝福大家在往后的工作與面試中一切順利。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。