溫馨提示×
您好,登錄后才能下訂單哦!
點擊 登錄注冊 即表示同意《億速云用戶服務條款》
您好,登錄后才能下訂單哦!
本篇文章為大家展示了Java中怎么實現一個二叉樹,內容簡明扼要并且容易理解,絕對能使你眼前一亮,通過這篇文章的詳細介紹希望你能有所收獲。
public class BinaryTreeLinked implements BinTree {protected BinTreeNode root;protected Strategy strategy;public BinaryTreeLinked(){ this(null); }public BinaryTreeLinked(BinTreeNode root) { this(root,new DefaultStrategy());}public BinaryTreeLinked(BinTreeNode root, Strategy strategy){this.root = root; this.strategy = strategy;
}
//返回樹的規模public int getSize() {return root==null?0:root.getSize();
}//判斷樹是否為空public boolean isEmpty() { return root==null;}//返回根結點引用public BinTreeNode getRoot() { return root;}//獲取樹的高度public int getHeight() { return isEmpty()?-1:root.getHeight();}//在樹中查找元素e,返回其所在結點public BinTreeNode find(Object e) {return searchE(root,e);
}//遞歸查找元素eprivate BinTreeNode searchE(BinTreeNode rt, Object e) {if (rt==null) return null;//如果是根結點,返回根if (strategy.equal(rt.getData(),e)) return rt;//否則在左子樹中找BinTreeNode v = searchE(rt.getLChild(),e); //沒找到,在右子樹中找if (v==null) v = searchE(rt.getRChild(),e); return v;
}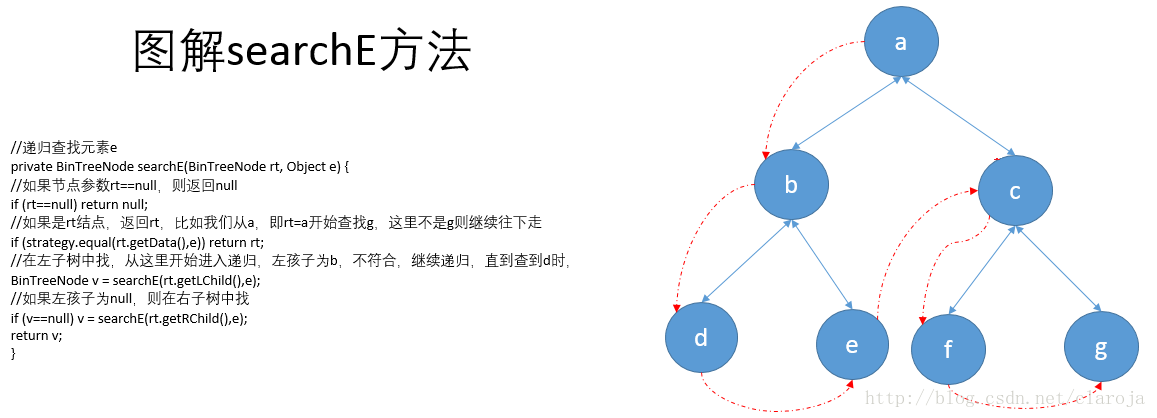
這里從e跳到c是難點,重要的是理解遞歸函數從最里層的遞歸函數,跳到最外層的函數。
//先序遍歷二叉樹public Iterator preOrder() {
LinkedList list = new LinkedListDLNode();
preOrderRecursion(this.root,list);return list.elements();
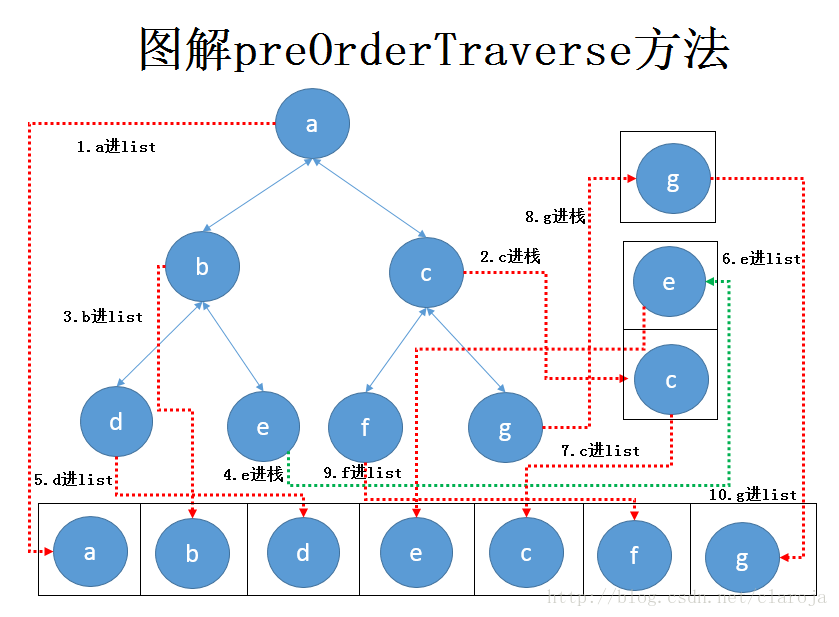
}//先序遍歷的遞歸算法private void preOrderRecursion(BinTreeNode rt, LinkedList list){if (rt==null) return; //遞歸基,空樹直接返回list.insertLast(rt); //訪問根結點preOrderRecursion(rt.getLChild(),list); //遍歷左子樹preOrderRecursion(rt.getRChild(),list); //遍歷右子樹}//先序遍歷的非遞歸算法private void preOrderTraverse(BinTreeNode rt, LinkedList list){if (rt==null) return;
BinTreeNode p = rt;Stack s = new StackSLinked();while (p!=null){while (p!=null){ //向左走到盡頭list.insertLast(p); //訪問根if (p.hasRChild()) s.push(p.getRChild()); //右子樹根結點入棧p = p.getLChild();
}if (!s.isEmpty()) p = (BinTreeNode)s.pop(); //右子樹根退棧遍歷右子樹}
}
//中序遍歷二叉樹 public Iterator inOrder(){ LinkedList list = new LinkedListDLNode(); inOrderRecursion(this.root,list); return list.elements(); } //中序遍歷的遞歸算法 private void inOrderRecursion(BinTreeNode rt, LinkedList list){ if (rt==null) return; //遞歸基,空樹直接返回 inOrderRecursion(rt.getLChild(),list); //遍歷左子樹 list.insertLast(rt); //訪問根結點 inOrderRecursion(rt.getRChild(),list); //遍歷右子樹 } //中序遍歷的非遞歸算法 private void inOrderTraverse(BinTreeNode rt, LinkedList list){ if (rt==null) return; BinTreeNode p = rt; Stack s = new StackSLinked(); while (p!=null||!s.isEmpty()){ while (p!=null){ //一直向左走 s.push(p); //將根結點入棧 p = p.getLChild(); } if (!s.isEmpty()){ p = (BinTreeNode)s.pop();//取出棧頂根結點訪問之 list.insertLast(p); p = p.getRChild(); //轉向根的右子樹進行遍歷 }//if }//out while } //后序遍歷二叉樹 public Iterator postOrder(){ LinkedList list = new LinkedListDLNode(); postOrderRecursion(this.root,list); return list.elements(); } //后序遍歷的遞歸算法 private void postOrderRecursion(BinTreeNode rt, LinkedList list){ if (rt==null) return; //遞歸基,空樹直接返回 postOrderRecursion(rt.getLChild(),list);//遍歷左子樹 postOrderRecursion(rt.getRChild(),list);//遍歷右子樹 list.insertLast(rt); //訪問根結點 } //后序遍歷的非遞歸算法 private void postOrderTraverse(BinTreeNode rt, LinkedList list){ if (rt==null) return; BinTreeNode p = rt; Stack s = new StackSLinked(); while(p!=null||!s.isEmpty()){ while (p!=null){ //先左后右不斷深入 s.push(p); //將根節點入棧 if (p.hasLChild()) p = p.getLChild(); else p = p.getRChild(); } if (!s.isEmpty()){ p = (BinTreeNode)s.pop(); //取出棧頂根結點訪問之 list.insertLast(p); } //滿足條件時,說明棧頂根節點右子樹已訪問,應出棧訪問之 while (!s.isEmpty()&&((BinTreeNode)s.peek()).getRChild()==p){ p = (BinTreeNode)s.pop(); list.insertLast(p); } //轉向棧頂根結點的右子樹繼續后序遍歷 if (!s.isEmpty()) p = ((BinTreeNode)s.peek()).getRChild(); else p = null; } } //按層遍歷二叉樹 public Iterator levelOrder(){ LinkedList list = new LinkedListDLNode(); levelOrderTraverse(this.root,list); return list.elements(); } //使用對列完成二叉樹的按層遍歷 private void levelOrderTraverse(BinTreeNode rt, LinkedList list){ if (rt==null) return; Queue q = new QueueArray(); q.enqueue(rt); //根結點入隊 while (!q.isEmpty()){ BinTreeNode p = (BinTreeNode)q.dequeue(); //取出隊首結點p并訪問 list.insertLast(p); if (p.hasLChild()) q.enqueue(p.getLChild());//將p的非空左右孩子依次入隊 if (p.hasRChild()) q.enqueue(p.getRChild()); } } }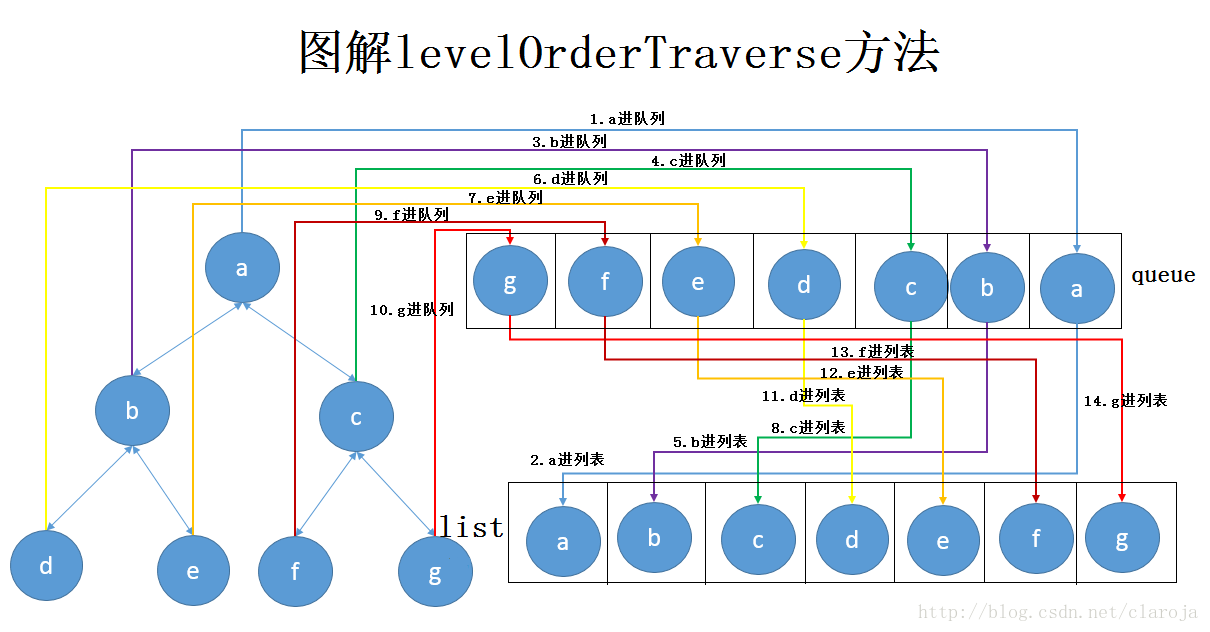
package dsa.adt;import dsa.adt.List;public interface BinTree {//返回樹的規模public int getSize();//判斷樹是否為空public boolean isEmpty();//返回根結點引用public BinTreeNode getRoot();//獲取樹的高度public int getHeight();//在樹中查找元素e,返回其所在結點public BinTreeNode find(Object e);//先序遍歷二叉樹public Iterator preOrder();//中序遍歷二叉樹public Iterator inOrder();//后序遍歷二叉樹public Iterator postOrder();//按層遍歷二叉樹public Iterator levelOrder();
}public class BinTreeNode implements Node {private Object data; //數據域private BinTreeNode parent; //父結點private BinTreeNode lChild; //左孩子private BinTreeNode rChild; //右孩子private int height; //以該結點為根的子樹的高度private int size; //該結點子孫數(包括結點本身)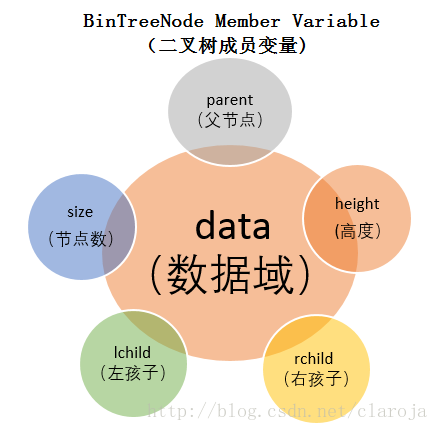
public BinTreeNode() {this(null);
}public BinTreeNode(Object e) {
data = e;
parent = lChild = rChild = null;
height = 0;
size = 1;
}
//獲得數據域public Object getData() { return data; }
//判斷是否有父親public boolean hasParent(){ return parent!=null;}
//判斷是否有右孩子public boolean hasRChild(){ return rChild!=null;}//判斷是否為某結點的左孩子public boolean isLChild(){ return (hasParent()&&this==parent.lChild);}//判斷是否為某結點的右孩子public boolean isRChild(){ return (hasParent()&&this==parent.rChild);}//取結點的高度,即以該結點為根的樹的高度public int getHeight() { return height; }//更新當前結點及其祖先的高度public void updateHeight(){int newH = 0;//新高度初始化為0,高度等于左右子樹高度加1中大的if (hasLChild()) newH = Math.max(newH,1+getLChild().getHeight());if (hasRChild()) newH = Math.max(newH,1+getRChild().getHeight());if (newH==height) return; //高度沒有發生變化則直接返回height = newH; //否則更新高度if (hasParent()) getParent().updateHeight(); //遞歸更新祖先的高度}這個更新高度的方法主要用于添加和刪除結點,遞歸的思想在這里使得代碼特別簡介優美。如果看不懂請結合下面的getParent、getLChild、getRChild方法來看。
//取以該結點為根的樹的結點數public int getSize() { return size; }//更新當前結點及其祖先的子孫數public void updateSize(){
size = 1; //初始化為1,結點本身if (hasLChild()) size += getLChild().getSize(); //加上左子樹規模if (hasRChild()) size += getRChild().getSize(); //加上右子樹規模if (hasParent()) getParent().updateSize(); //遞歸更新祖先的規模}updateSize和updateHeight是一對兄弟方法。
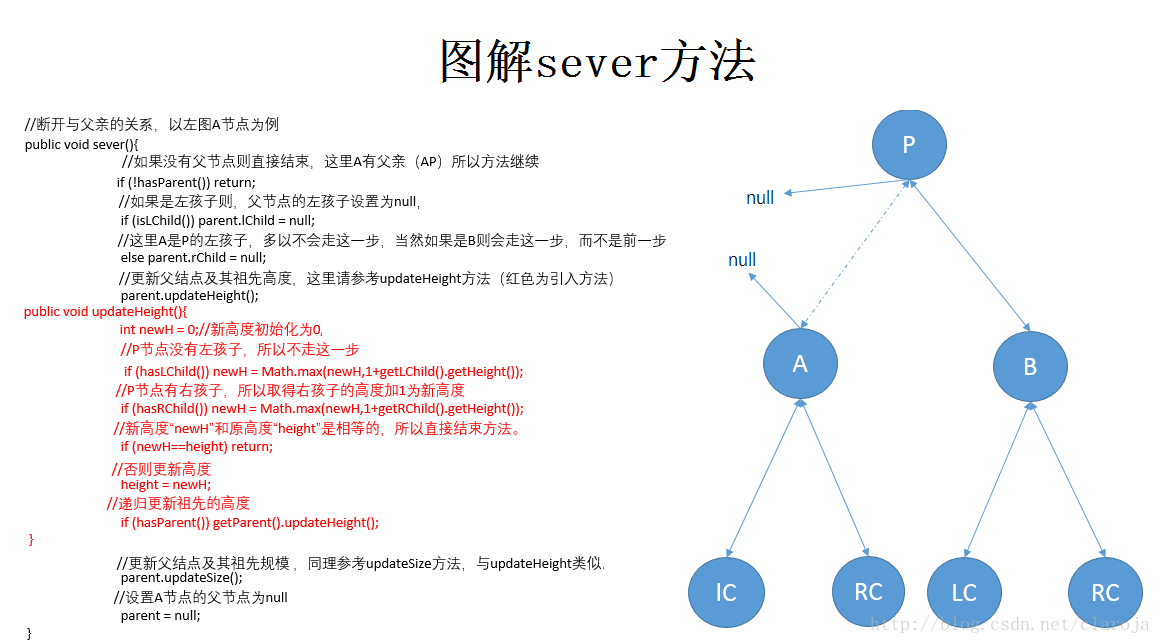
//取父結點public BinTreeNode getParent() { return parent; }//斷開與父親的關系public void sever(){if (!hasParent()) return;//如果沒有父節點則直接結束if (isLChild()) parent.lChild = null;//如果是左孩子則,父節點的左孩子設置為nullelse parent.rChild = null;parent.updateHeight(); //更新父結點及其祖先高度parent.updateSize(); //更新父結點及其祖先規模parent = null;
}
//取左孩子public BinTreeNode getLChild() { return lChild; }//設置當前結點的左孩子,返回原左孩子public BinTreeNode setLChild(BinTreeNode lc){
BinTreeNode oldLC = this.lChild;if (hasLChild()) { lChild.sever();} //斷開當前左孩子與結點的關系if (lc!=null){
lc.sever(); //斷開lc與其父結點的關系this.lChild = lc; //確定父子關系lc.parent = this;this.updateHeight(); //更新當前結點及其祖先高度this.updateSize(); //更新當前結點及其祖先規模}return oldLC; //返回原左孩子}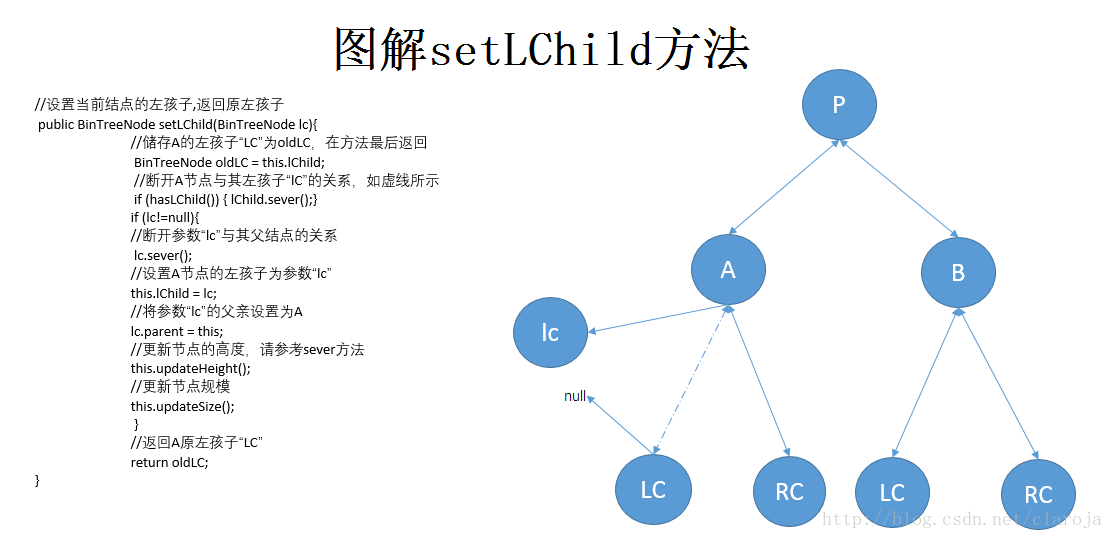
//取右孩子public BinTreeNode getRChild() { return rChild; }//設置當前結點的右孩子,返回原右孩子public BinTreeNode setRChild(BinTreeNode rc){
BinTreeNode oldRC = this.rChild;if (hasRChild()) { rChild.sever();} //斷開當前右孩子與結點的關系if (rc!=null){
rc.sever(); //斷開lc與其父結點的關系this.rChild = rc; //確定父子關系rc.parent = this;this.updateHeight(); //更新當前結點及其祖先高度this.updateSize(); //更新當前結點及其祖先規模}return oldRC; //返回原右孩子}
}設置右孩子方法與設置左孩子方法類似,請參考setLChild方法。
package dsa.adt;public interface Node {//獲取結點數據域public Object getData();//設置結點數據域public void setData(Object obj);
}package dsa.strategy;public interface Strategy {//判斷兩個數據元素是否相等public boolean equal(Object obj1, Object obj2);/** * 比較兩個數據元素的大小 * 如果obj1 < obj2 返回-1 * 如果obj1 = obj2 返回0 * 如果obj1 > obj2 返回1 */public int compare(Object obj1, Object obj2);
}package dsa.strategy;public final class DefaultStrategy implements Strategy {public boolean equal(Object obj1, Object obj2)
{return obj1.toString().equals(obj2.toString());
}public int compare(Object obj1, Object obj2)
{int comp = obj1.toString().compareTo(obj2.toString());if (comp==0) return 0;else if (comp>0) return 1;else return -1;
}
}上述內容就是Java中怎么實現一個二叉樹,你們學到知識或技能了嗎?如果還想學到更多技能或者豐富自己的知識儲備,歡迎關注億速云行業資訊頻道。
免責聲明:本站發布的內容(圖片、視頻和文字)以原創、轉載和分享為主,文章觀點不代表本網站立場,如果涉及侵權請聯系站長郵箱:is@yisu.com進行舉報,并提供相關證據,一經查實,將立刻刪除涉嫌侵權內容。