Boyer Moore算法怎么用

Boyer Moore算法怎么用，相信很多沒有經驗的人對此束手無策，為此本文總結了問題出現的原因和解決方法，通過這篇文章希望你能解決這個問題。

簡介

對于字符串的搜索算法，我曾經討論過KMP算法的思路和實現。 KMP算法的實現思路是基于模式串里面的的前綴和后綴匹配，這種算法的效率已經足夠快了。沒想到的是，這里我們要討論的Boyer Moore算法效率更加驚人。

思路分析

在之前的算法里，我們是通過從模式串的開頭到結尾這么一個個的去和目標串比較，這種方式在碰到匹配的元素時則繼續比較下一個，在沒有匹配的時候，則通過查找模式表構建的匹配表來選擇模式串里后面的第幾個元素來繼續進行比較。這樣目標串里的索引就不用往回挪。但是，這里比較的順序恰好相反。假設目標串長度為n, 模式串長度為m。那么，首先我們就從兩個串的m - 1索引位置開始比較，如果相同，則一直向前，如果不同，則需要根據這個不同的字符的情況來判斷。

根據比較字符的不同，我們可能有兩種情況，一種是這個不同的字符不在模式串里。那么很顯然，模式串里任何一個字符都不可能和它匹配的，我們只需要跳到這個字符的后面那個位置開始繼續比較就可以了。還有一種情況就是這個字符是在模式串里的，那么，我們就需要找到和這個字符匹配的最后一個出現在模式串里的字符。這樣，我們可以在模式串中從最后匹配的位置開始繼續往后比較。

前面的這部分描述顯得比較抽象，我們可以結合一個具體的示例來討論。假設我們有字符串s和p，s的值為：FINDINAHAYSTACKNEEDLEINA, p的值為: NEEDLE。我們分別用i, j來表示s, p當前的位置。那么，他們比較的過程如下圖：

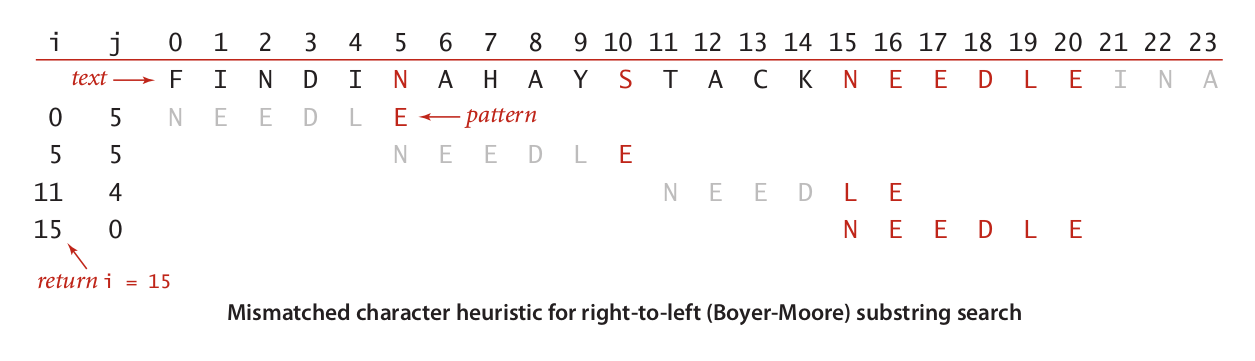
結合上圖來說，他們最開始比較的位置是從索引5開始。這個時候s在這個位置的元素是N，而p在這個位置的字符是E。那么他們并不匹配。我們就需要跳到后面進行比較。而這個字符N在p里面是存在的，對應p里最后出現N的位置就是索引0。所以我們就從N的這個位置開始到p最末尾的位置作為比較的點，又從p的末尾和對應的s的位置進行比較。這個時候i的索引位置為10的時候它和p最末尾的字符E并不匹配，而且這個字符是S，在p串里也找不到對應的字符。那么這時候，我們就需要從S后面的元素開始和p的第一個元素對齊，然后我們再從p的最后一個元素以及s串的索引i + j進行比較。這時候一直比較到開頭，發現有匹配的串。于是返回i = 15。

概括

經過上述的討論，我們發現，要實現這個算法需要考慮的就是怎么用一種比較簡單的方法將字符串的匹配和不匹配場景給統一起來。這樣在每次比較到匹配或者不匹配的時候能夠對應的調整。對于前面的場景我們來仔細看一下。

當比較的字符和當前p模式串里的字符不匹配時，如果這個不匹配的字符也不在模式串里，那么這種情形的調整如下圖：

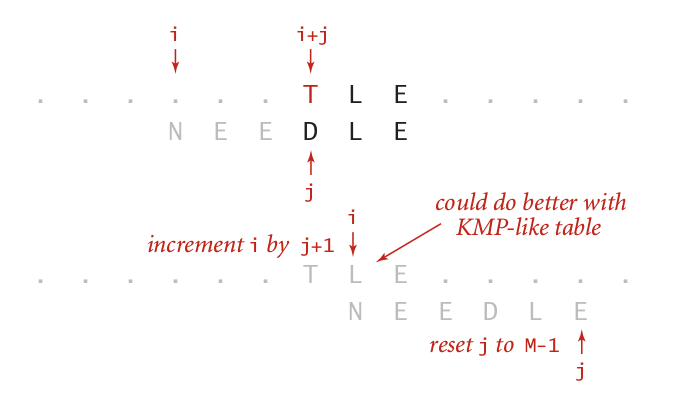
因為這種情況下，無論取模式串里的那個元素都不可能和這個元素匹配的，所以相當于要將整個模式串挪到這個元素的后面的那個位置對齊再來比較。這個時候，相當于將j重置到m - 1的值，而這個時候i的值也調整到i + j + 1 。

還有一種情況就是這個當前不匹配的字符在模式串里，如下圖：

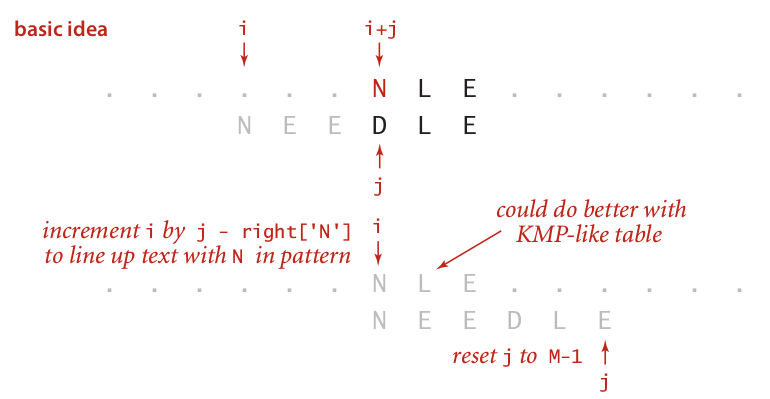
在這個示例里，因為不匹配的字符是N，但是N存在于模式串中。所以我們需要將i所在的位置移動到這個不匹配元素的位置。而這個時候模式串里的位置是j，如果我們可以找到N所在的索引位置，就可以通過j - right['N']來實現了。

所以總的來說，我們在比較的時候對于目標串的索引i和模式串的索引j來說，它們比較和調整順序正好相反。i是逐步遞增的調整，而j是遞減的進行比較。當s.charAt(i + j) == p.charAt(j)的時候，表示它們匹配。所以這時候繼續進行個j--這個操作進行下一步比較就可以。而s.charAt(i + j) != p.charAt(j)的時候，就要調整了。根據前面的討論，如果s.charAt(i + j)不存在于p中間，這個時候，我們需要將i往右移動j + 1個位置。按照前面討論的，也就是j - right[s.charAt(i + j)]。這也說明了right[s.charAt(i + j)] 為-1。

而如果s.charAt(i + j)存在于模式串中，那么我們需要找到這個字符在模式串中間的位置，我們需要移動的距離就是從j到這個字符的距離。如果用j - right[s.charAt(i + j)]，那么這里right[s.charAt(i + j)]記錄的應該就是字符s.charAt(i + j)在模式串中的位置。

這樣，我們將right[]數組記錄的值統一起來了。問題的核心就歸結為怎么計算right數組。

計算right

計算right數組的過程比較簡單，因為只要記錄每個字符在模式串里最后出現的位置就可以了。對于不在模式串里的元素呢，只要設置為-1就可以了。所以我們可以用如下一段代碼實現：

1. right = new int[r];  

2. for(int c = 0; c < r; c++)  

3.     right[c] = -1;  

4. for(int j = 0; j < m; j++)  

5.     right[pat.charAt(j)] = j;  

最終實現

剩下的就是將整個實現給連貫起來。建立好right數組之后，剩下的就是從目標串i開始，每次比較s[i + j]和p[j]的位置。如果相等，就繼續比較，直到j == 0。如果不等，則計算i后面要移動的距離skip，其中skip = j - right[s[i + j]]。這樣，詳細的實現如下：

1. public class BoyerMoore {  

2.     private int[] right;  

3.     private String pat;  

4.   

5.     public BoyerMoore(String pat) {  

6.         this.pat = pat;  

7.         int m = pat.length();  

8.         int r = 256;  

9.         right = new int[r];  

10.         for(int c = 0; c < r; c++)  

11.             right[c] = -1;  

12.         for(int j = 0; j < m; j++)  

13.             right[pat.charAt(j)] = j;  

14.     }  

15.   

16.     public int search(String txt) {  

17.         int n = txt.length();  

18.         int m = pat.length();  

19.         int skip;  

20.         for(int i = 0; i <= n - m; i+= skip) {  

21.             skip = 0;  

22.             for(int j = m - 1; j >= 0; j--) {  

23.                 if(pat.charAt(j) != txt.charAt(i + j)) {  

24.                     skip = j - right[txt.charAt(i + j)];  

25.                     if(skip < 1) skip = 1;  

26.                     break;  

27.                 }  

28.             }  

29.             if(skip == 0) return i;  

30.         }  

31.         return -1;  

32.     }  

33. }  

在上述的代碼實現里，還有一個值得注意的小細節，就是計算出skip之后，要判斷skip是否小于1。因為有可能碰到的當前不匹配字符是存在于模式串里，但是它最后出現的位置要大于當前的值j了。這時候，我們要保證i最少要移動一位。所以這里要設置為1。 

還有一個需要注意的地方就是，因為要考慮到為每個字符建立它的映射關系，所以我們需要建立一個有字符集長度那么長的right數組。在字符集太大的情況下，它占用的空間會比較多。這里只是針對理想的256個字符的情況建立的right表。

從該算法的性能來說，它在理想的情況下的時間復雜度為O(M/N) 其中M是目標串的長度，而N是模式串的長度。

Boyer Moore算法是一個在實際中應用比較廣泛的算法，它的速度更加快。和其他的字符串匹配方法比起來，它采用從后面往前的比較方式。同時通過建立一個字符映射表來保存字符在當前模式串里的位置，以方便每次比較的時候源串的位置調整。它最大的特點就是不再是一個個字符的移動，而是根據計算一次跳過若干個字符。這樣總體的性能比較理想。

看完上述內容，你們掌握Boyer Moore算法怎么用的方法了嗎？如果還想學到更多技能或想了解更多相關內容，歡迎關注億速云行業資訊頻道，感謝各位的閱讀！