Ceph中CRUSH算法的示例分析

這篇文章主要介紹Ceph中CRUSH算法的示例分析，文中介紹的非常詳細，具有一定的參考價值，感興趣的小伙伴們一定要看完！

一、bucket數據結構介紹。

     struct crush_bucket {

          __s32      id;          //bucket的ID號，crushmap中所有bucket的編號都是負數

          __u16      type;     //bucket的類型(uniform/list/tree/straw/straw2)

          __u8        alg;       //bucket使用的算法

          __u8        hash;      //bucket使用哪種hash算法

          __u32      weight;     //bucket權重值

          __u32      size;          //bucket中包含的items的數量

          __s32      *items;      //bucket中包含的items內容

          __u32      perm_x;     //緩存進行隨機排列的輸入值

          __u32      perm_n;     //緩存隨機排列結果perm中可用的個數

          __u32      *perm;       //對bucket中items的緩存隨機排列結果

     };

二、uniform類型。

     1、uniform類型bucket的數據結構。

          struct crush_bucket_uniform {

               struct crush_bucket h;          //通用bucket定義

               __u32      item_weight;          //uniform bucket中所有items的權重值(uniform類型的bucket，其所有items的權重值是一樣的)

          };

     2、uniform類型bucket算法分析。

          輸入參數：

               1）crush_bucket_uniform結構；

               2）待執行運算的輸入值x；

               3）輸入值x的副本位置r；

          輸出參數：

               1）經過uniform算法計算后的bucket中的item；

          算法分析：

               1）對于第一次執行uniform算法來說，經過hash()函數計算出來一個隨機數后對bucket.h.size取模，得到一個隨機的item位置，之后將這個隨機位置寫入到bucket.h.perm[0]中且返回該隨機數指定的bucket.h.item；

               2）對于后續執行uniform算法來說，由于bucket.h.perm[]中已經有隨機數且bucket.h.perm_n中保存bucket.h.perm[]中可用的隨機數的個數，因此，對于副本位置r來說，若r%bucket.h.size<bucket.h.perm_n，則直接從bucket.h.perm[r%bucket.h.size]獲取隨機數，之后返回該隨機數指定的bucket.h.item。若r%bucket.h.size>=bucket.h.perm_n，則需要執行hash()函數計算出來一個隨機數后對(bucket.h.size-bucket.h.perm_n)取模，得到i，之后將bucket.h.perm[]中bucket.h.perm_n+i與bucket.h.perm_n位置的內容互換，之后bucket.h.perm_n++，反復執行，直到r%bucket.h.size < bucket.h.perm_n。最后從bucket.h.perm[r%bucket.h.size]獲取隨機數，之后返回該隨機數指定的bucket.h.item；

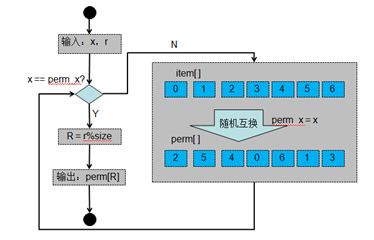
uniform類型算法流程圖

     3、uniform算法適用條件。

          1）bucket中所有的items的權重是一樣的，也就是說uniform算法不考慮權重；

          2）uniform算法適合bucket中的item不經常變更的情況，若經常變更則bucket.h.size會變化，從而導致bucket.h.perm_n需要重新計算，數據會大面積的遷移；

三、list類型。

     1、list類型bucket的數據結構。

          struct crush_bucket_list {

               struct crush_bucket h;          //通用bucket定義

               __u32     *item_weight;          //bucket中每個item的權重值

               __u32     *sum_weight;          //bucket中從第一個item開始到第i個item的權重值之和

          };

     2、list類型bucket算法分析。

          輸入參數：

               1）crush_bucket_list結構；

               2）待執行運算的輸入值x；

               3）輸入值x的副本位置r；

          輸出參數：

               1）經過list算法計算后的bucket中的item；

          算法分析：

               1）從bucket中最后一個item開始反向遍歷整個items，執行hash()函數計算出一個隨機數w；

               2）將該隨機數w乘以bucket.sum_weight[i]，之后將結果右移16位；

               3）判斷右移16位后的結果和bucket.item_weight[i]，若結果小于bucket.item_weight[i]則直接返回bucket.h.items[i]，否則反向遍歷bucket中下一個item；

               4）若所有右移16位后的結果都大雨bucket.sum_weight[i]，則最終返回bucket.h.items[0]；

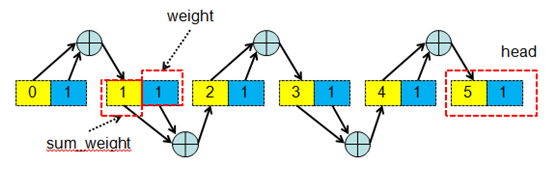
list類型算法原理圖

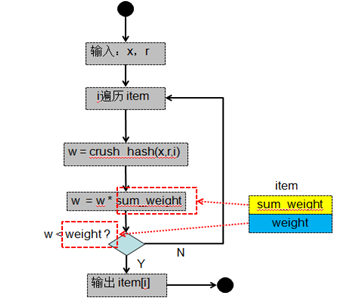
list類型算法流程圖

     3、list算法適用條件。

          1）適用于集群拓展類型。當增加item時，會產生最優的數據移動。因為在list bucket中增加一個item節點時，都會增加到head部，這時其他節點的sum_weight都不會發生變化，只需要將old_head 上的sum_weight和weight之和添加到new_head的sum_weight就好了。這樣時其他item之間不需要進行數據移動，其他的item上的數據 只需要和 head上比較就好，如果算的w值小于head的weight，則需要移動到head上，否則還保存在原來的item上。這樣就獲得了最優最少的數據移動；

          2）list bucket存在一個缺點，就是在查找item節點時，只能順序查找 時間復雜度為O(n)；

四、tree類型。

     1、tree類型bucket的數據結構。

          struct crush_bucket_tree {

               struct crush_bucket h;          //通用bucket定義

               __u8      num_nodes;             //記錄node_weights中的所有節點個數(包括二叉樹中間節點和葉子節點)

               __u32      *node_weights;      //除了bucket中item的權重值外，node_weights中還包含一個二叉樹結構的權重值，其中bucket中的item是樹的葉子節點，二叉樹的中間節點的權重值是左右兩個字節點權重值之和

          };

     2、tree類型bucket算法分析。

          輸入參數：

               1）crush_bucket_tree結構；

               2）待執行運算的輸入值x；

               3）輸入值x的副本位置r；

          輸出參數：

               1）經過tree算法計算后的bucket中的item；

          算法分析：

               1）找到二叉樹的根節點，即：n=bucket.num_nodes >> 1；

               2）判斷當前節點是否是葉子節點，若不是則從bucket.node_weights[n]中得到二叉樹上對應中間節點的權重值，之后執行hash()函數的到一個隨機數，之后將這個隨機數乘以中間節點的權重值，再右移32位。將經過調整后的權重值與該中間節點左子樹的權重值進行比較，若小于左子樹的權重值則從左子樹開始遍歷，否則從柚子樹開始遍歷；

               3）當前節點到達葉子節點，則返回該葉子節點指定的item，即：bucket.h.items[n>>1]；

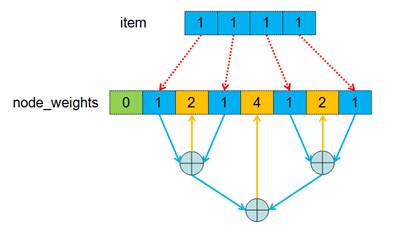
tree類型算法原理圖

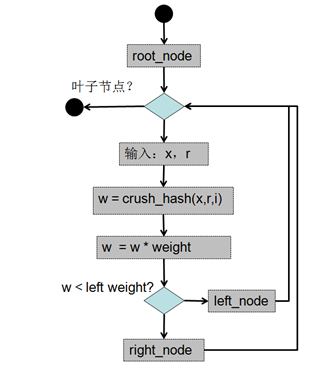
tree類型算法流程圖

     3、tree算法適用條件。

          1）使用tree算法時定位數據的時間復雜度為O(logn)，這使其適用于管理大得多設備數量或嵌套buckets；

        2）樹狀buckets是一種適用于任何情況的buckets，兼具高性能與出色的重組效率；

五、straw類型。

     1、straw類型bucket的數據結構。

          struct crush_bucket_straw {

               struct crush_bucket h;          //通用bucket定義

               __u32      *item_weights;       //保存bucket中所有item的權重值

               __u32      *straws;                 //保存根據item權重值計算出來的權重值

     2、straw類型bucket算法分析。

          輸入參數：

               1）crush_bucket_straw結構；

               2）待執行運算的輸入值x；

               3）輸入值x的副本位置r；

          輸出參數：

               1）經過straw算法計算后的bucket中的item；

          算法分析：

               1）順序遍歷backet中所有的items，對于bucket中每一個item執行hash()算法計算出一個隨機數，之后將該隨機數與bucket.staws[i]相乘，得到一個修正后的隨機值；

               2）比較bucket中所有items經過hash()算法算出的修正后的隨機值且找到最大的修正后的隨機值；

               3）返回最大的修正后的隨機值位置所在的item，即：bucket.h.item[high]；

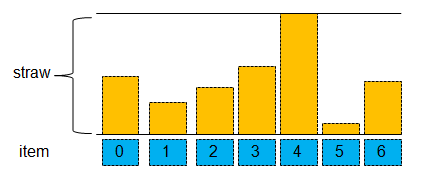
straw算法原理圖

     3、straw數組的生成過程分析。

          1）根據bucket.item_weights[bucket.h.size]數組，生成一個按照items權重值從小到大排序的數組reverse[bucket.h.size]且reverse[bucket.h.size]中保存的是按序排列的item權重值的下標；

          2）初始化計算straw算法所使用的變量。

               numleft=bucket.h.size;

               straw=1.0;

               lastw=0;

               wbelow=0;

          3）遍歷整個items，按照如下算法計算items對應的straw值。

               A）對于bucket.item_weights[reverse[i]]==0，則straw[reverse[i]]=0；

               B）設置straw值。bucket.straw[reverse[i]]=straw*0x1000；

               C）變量i＋1；

               D）計算wbelow值。wbelow=(bucket.item_weights[reverser[i-1])-lastw)*numleft；

               E）變量numleft-1；

               F）計算wnext值。wnext=numleft*(bucket.item_weights[reverse[i]-bucket.item_weight[revese[i-1])；

               G）計算pbelow值。pbelow=wbelow/(wbelow+wnext)；

               H）計算straw值。straw=pow(1/pbelow,1/numleft)；

               I）計算lastw值。lastw=bucket.item_weights[reverse[i-1]]；

          對于bucket中所有的items來說，權重越大，計算出來的straw值就越大；

          從算法來看，計算item的straw值與item的權重值以及item之前的權重值有關，因此在修改bucket中某一個item的權重值時會影響該item及其前后items的straw值；

     4、straw算法適用條件。

          1）考慮權重對數據分布的影響，即：權重值高的item來說，被選中的概率就大，落在權重值高的item的數據越多；

          2）straw類型的buckets可以為子樹之間的數據移動提供最優的解決方案；

六、straw2類型。

     1、straw2類型bucket的數據結構。

          struct crush_bucket_straw2 {

               struct crush_bucket h;           //通用bucket定義

               __u32      *item_weights;       //保存bucket中所有item的權重值

          };

     2、straw2類型bucket算法分析。

          輸入參數：

               1）crush_bucket_straw2結構；

               2）待執行運算的輸入值x；

               3）輸入值x的副本位置r；

          輸出參數：

               1）經過straw2算法計算后的bucket中的item；

          算法分析：

               1）遍歷整個bucket的所有items，得到items對應的權重值；

               2）對于非零權重值來說，首先執行hash()函數計算出一個隨機數，之后將該隨機數作為參數調用最小指數隨機變量分布算法得到的結果再減去0x1000000000000，最后將該結果除以item權重值得到item對應的最終值(draw)。對于權重值為零來說，最終值(draw)為最小值；

               3）比較整個bucket中所有items計算出來的最終值(draw)，取最終值最大的item，即：bucket.h.items[high]；

               從算法來看，計算item的straw值只與item的權重值有關，與bucket中其它items的權重值無關。因此在修改bucket中某一個item的權重值時不會影響該bucket中其它items的straw值；

     3、straw2算法適用條件。          

          1）考慮權重對數據分布的影響，即：權重值高的item來說，被選中的概率就大，落在權重值高的item的數據越多；

          2）straw類型的buckets可以為子樹之間的數據移動提供最優的解決方案；

        3）適合bucket中的items權重動態變化的場景；

以上是“Ceph中CRUSH算法的示例分析”這篇文章的所有內容，感謝各位的閱讀！希望分享的內容對大家有幫助，更多相關知識，歡迎關注億速云行業資訊頻道！